Calculating the first four moments can help us get a lot of distribution insights (And hence? are worth your moment? Woah!)
Below is a brief overview of what each of the four statistical moments represent (And a bit of banter from Steve, ignore him):
?Steve, you better be all ears now, or I am gonna tell your step-dad?
- First Moment (Mean): The central tendency of the observations. It?s the sum of the products of observations and their probabilities of occurrence aka. the average value.
?Yeah, everybody knows it already Steve but I gotta go one step at a a time?
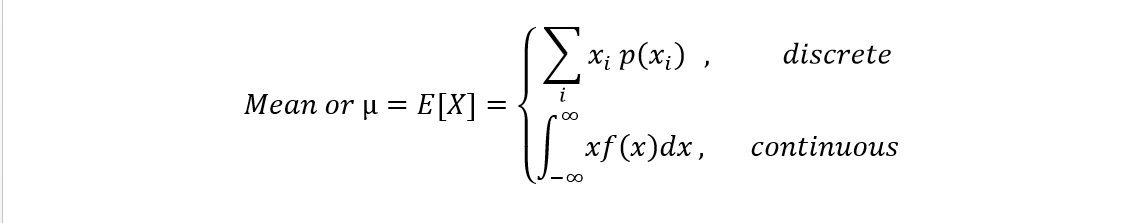
The following moments have prefixes ?central? and ?standardized?:
Central ? moment about the mean (refer to the first picture above)
Standardized ? implies moments are calculated after the distributions are normalized.
2. Second Central Moment (Variance): Spread of the observations from the average value i.e. the squared deviation of the random variable from its mean.
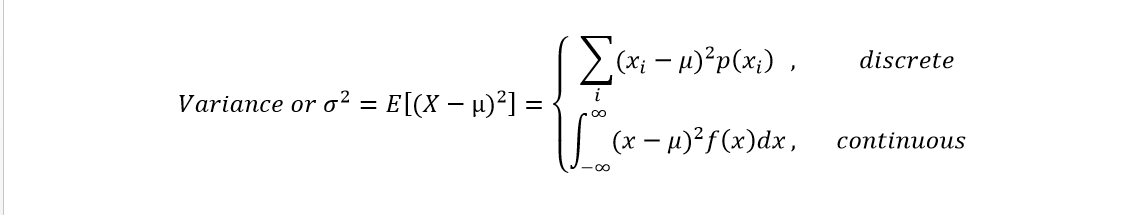
?Ffs Steve, mind giving that leather-beating shop of a mouth some rest? I know this is old info, the new stuff is coming alright, calm it?
3. Third Standardized Moment (Skewness): Skewness gives an idea of the symmetry of the probability distribution around the mean.
For large enough sample sizes (>300), the values for skewness between -2 and +2 are considered acceptable in order to prove that a distribution is a normal uni-variate distribution.
For smaller sample sizes, you will have to convert the observations to z-values and do additional operations (It is better to stick to K-S tests or Q-Q plots).
?You might as well give up on this Steve, not your cup of tea. Lad was looking for something new, innit??
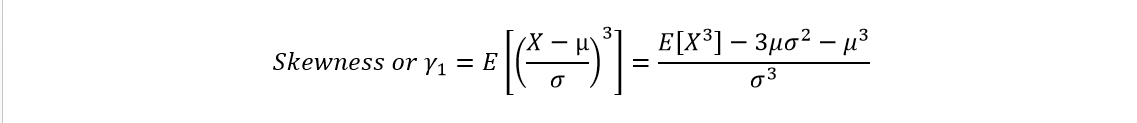
a) In case of a positive value, mean is to the right of the peak (mode).
b) A value of zero implies the mean coincides with the median and the mode (as in the case of symmetric distributions like normal distributions).
c)A negative value implies the mean is to the left of the peak (mode),
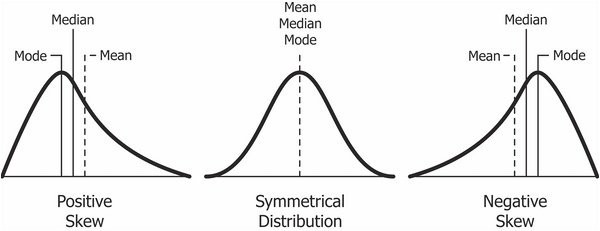Stevie remembers better when there are pictures. I nicked this one off here. Things I do for this kid!
4. Fourth Standardized Moment (Kurtosis) : Kurtosis gives an idea of how fat/heavy are the tails of a distribution, i.e how frequent extreme deviations (or outliers) are from the average value.
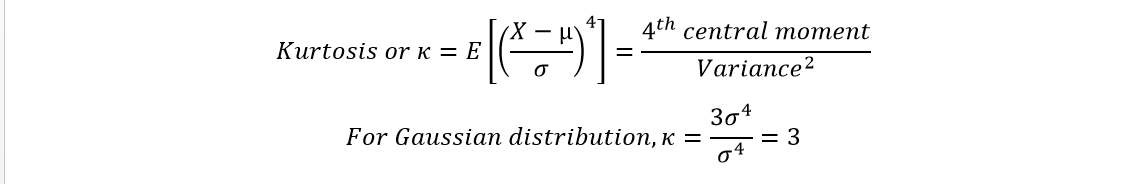
Generally, the fourth moment is subtracted by 3. This modified kurtosis, a cumulant, is called excess kurtosis.
Excess kurtosis is preferred over kurtosis by some statisticians due to its easy comparability with the Gaussian distribution and its extensive nature (formulas related to extensive property are more naturally expressed in terms of the excess kurtosis)
?I don?t know what I am talking about here. Don?t you smirk Steve , I can see you haven?t flossed in days.?
a) A value of zero (Mesokurtic) implies the tails die down similar to normal distributionsb) A negative value (Platykurtic) implies fatter tails or more extreme deviations from the mean (e.g. Uniform distribution) and,c) A positive value (Leptokurtic) implies thinner tails (e.g. Laplace distribution)
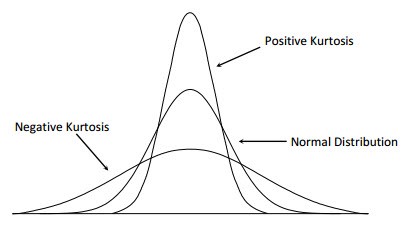Excess Kurtosis: Tailedness of a distribution as compared to the normal distribution (Source)
?Steve, wake the hell up. Gosh, who am I even doing this tutorial for. Oh come-on man, don?t start crying again. God!?
