You?ve heard it time and time again, ?Rationalize the denominator. Make sure to rationalize the denominator!? But why??? Who decided that getting the root out of the denominator and into the numerator was the thing to do?
Here are three reasons why RTD became the standard from Algebra to Calculus.
The Commonsense Reason
The standard reason why you need to RTD is perfectly practical. As you?ve most likely discovered, in mathematics you can often write solutions in multiple different ways and forms. All of these variations are cool, but for practical purposes, they make life more difficult for those grading your papers.
Defining and requiring a standard form for answers saves your teacher the time-consuming headache of having to verify that your solution is equivalent to the answer key, or even worse, accidentally marking your answer incorrect!
Just like reducing a fraction to its simplest form, RTD is the protocol for simplifying fractions with roots in the denominator.
The Reasonable Reason
A commonly defined nomenclature makes sense and all, but still leaves us with the question: why have we decided that having a root in the numerator is okay, but having a root in the denominator is not??
Why is (2 ?3) / 3 the simpler form of 2 / ?3 ?

The reason is that if we need to add or subtract fractions with radicals, it?s easier to compute if there are whole numbers in the denominator instead of irrational numbers. For example, it?s easier to add (2?3/3) + (( 3??2)/7) than the non-rationalized version: (2/?3) +(1 / (3 + ?2)).
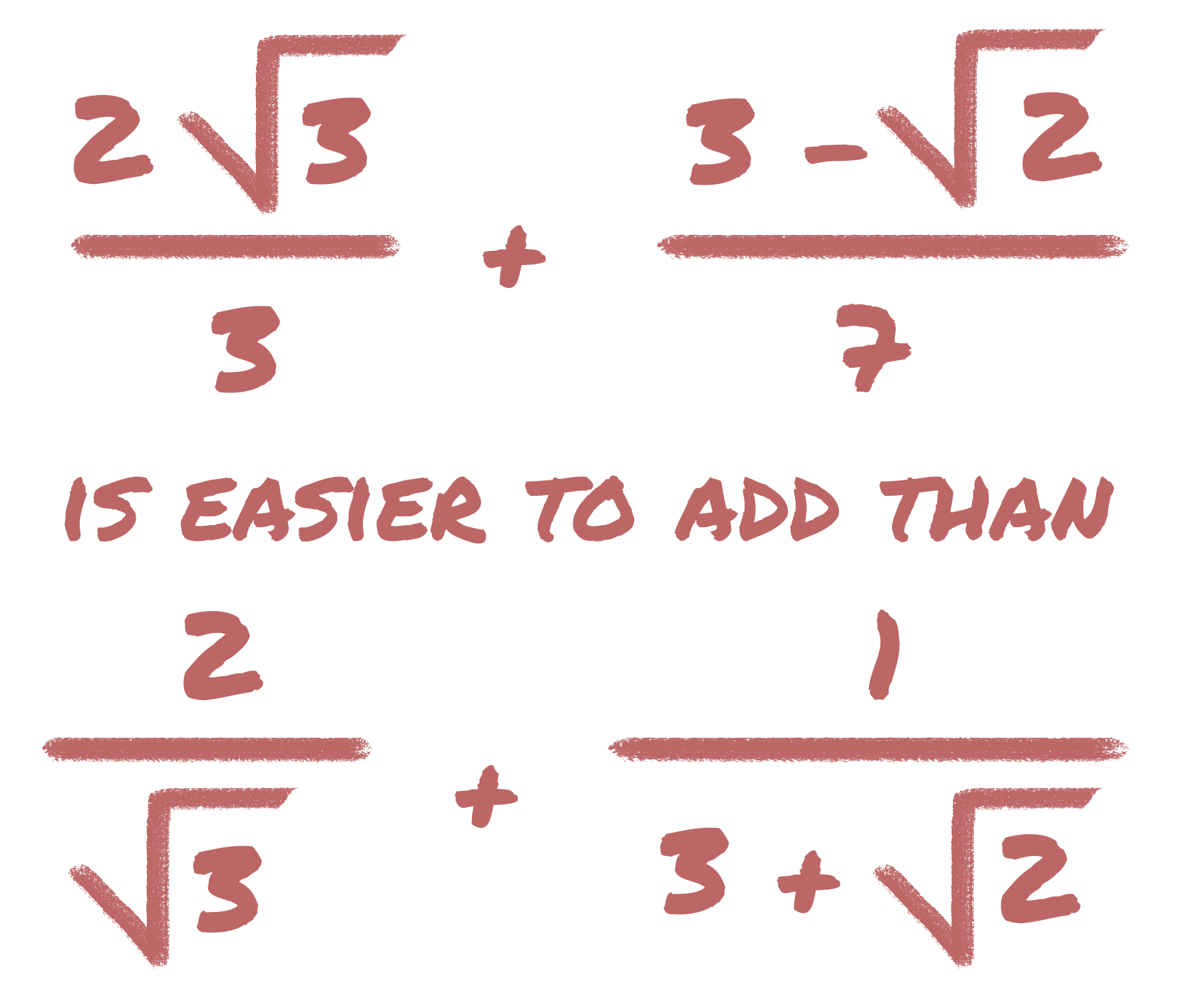
To add the first set of fractions together all we need to do is make a common denominator of 21 and then add like terms from the numerators. It?s not nearly as clear what the common denominator is of the second set of fractions.
To solve the second problem you would most likely rationalize the denominator first and then make the common denominator of 21 before adding the fractions together.
So RTD provides a common form for comparing and grading solutions as well as makes it easier for us to perform further computations by hand when needed.
The Historical Reason
At this point you may be thinking, ?Why not just leave the roots in the denominator and rationalize them if and when I need to add or subtract the fractions??
And yes, that?s a valid point. That?s why perhaps the best answer to why we are so often required to RTD is the historical one. The answer that takes us back to life before computers and calculators were ubiquitous. Back when people had to routinely do division? by hand! *gasp!*
Let?s take a look at our two equivalent fractions from above:

What would happen if we actually wanted to divide these fractions?
Let?s begin by dividing 2/?3 by hand.
Before calculators, you would begin by using an algorithm to find an approximation of ?3 by hand which is 1.73205081? After approximating ?3, you would then set up your long division.

If this looks complicated to you, that?s because it is. Having an irrational number as the divisor is practically unheard of.
In order to perform this division, you would need to decide how many decimal places you want to keep around, round to that decimal place, then you would need to multiply both the dividend and divisor by a large enough power of ten to make your divisor a whole number. After doing all that you could then proceed with the messy task of dividing those two unwieldy numbers.
Now let?s take a look at how we?d go about dividing the equivalent, rationalized fraction: (2?3)/3.
Without a calculator, you?d begin by computing the approximation for ?3 like above, which is 1.73205081? Next, you would multiply 1.73205081? by 2 to get 3.46410162? Then simply set up your division.

This is much easier to divide by hand! We don?t have to do any prep work, we can jump directly into the division problem.
And most importantly, HOW to RTD 🙂
Now that you understand why it?s so important to RTD, you may want to practice up on it!
This first tutorial explains how to rationalize the denominator with a standard square root, then moves on to demonstrate how to handle the trickier scenario of rationalizing the denominator when you have the sum or difference of a whole number and a square root in the denominator. To do this you?ll be introduced to the conjugate.
Subscribe to Math Hacks on YouTube
In this second tutorial, you?ll learn how to rationalize more difficult denominators with cube roots and fourth roots. We?ll also talk about how you can use the alternate fractional exponent notation to simplify the process.
Subscribe to MathHacks on YouTube
Need More Math Help??
- Check out Math Hacks on YouTube for more hands-on math tutorials covering popular topics from Algebra, Trigonometry, Precalculus, Calculus, & Advanced Math.
- You can find a number of interesting math topics and problems right here on Medium, just click that follow button!
Thanks for joining me!
? Brett