Cryptography
Cryptography is the process of converting a plain text into unreadable encrypted form using encryption techniques thereby protecting information while communicating over the public network. Keys are used to encrypt or decrypt the data. Based on the types of keys used we can divide encryption techniques into two types:
1.Symmetric2.Asymmetric
Symmetric Cryptography
In this type of cryptography, same key is used to encrypt or decrypt the data. Sender will encrypts the data using shared secret key K and receiver will decrypt the data using the same shared key K.
Asymmetric Cryptography
In this type, two keys are used in the whole process private key and public key. The public is used to encrypt the data and private key is used to decrypt the data.The public key will be available to all over the network. Suppose Alice wants to communicate with Bob. Alice now can encrypt its information using Bob?s publicly available public key and send it to Bob. Now, Bob has the private key which he can use it to decrypt the original message. Only the private key is used to decrypt the cipher text.
Diffie-Hellman Key Exchange Mechanism
Diffie Hellman algorithm is an asymmetric algorithm used to establish a shared secret for a symmetric key algorithm. Nowadays most of the people uses hybrid crypto system i.e, combination of symmetric and asymmetric encryption. Asymmetric Encryption is used as a technique in key exchange mechanism to share secret key and after the key is shared between sender and receiver, the communication will take place using symmetric encryption. The shared secret key will be used to encrypt the communication.
You?re not sharing information during the key exchange, you?re creating a key together.
Pictorial Representation:
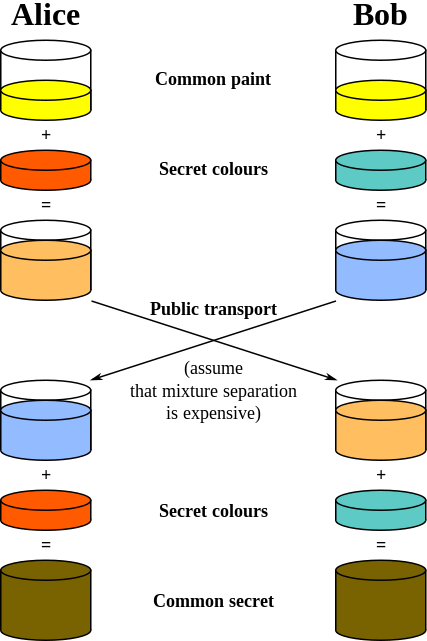Source : Wikipedia
Let?s dive into maths.
Scenario :
Alice and Bob wants to communicate securely. How Diffie Hellman Algorithm can help their communication?
Process:
We know Diffie Hellman algorithm is an asymmetric algorithm. So Alice and Bob will agree to a public key pair (g, p) where g is the generator and p is the prime modulus.
Let?s assume they chose g=3 and p=17. Now the public key pair (3,17) will be available public over the network.
Alice: Alice will choose a random private number lets assume Apriv=15 and she will do the exponentiation and modulus operation with public key pair and her private key.
g^Apriv mod p
3? mod 17=6 ??..eq1 Now the number 6 will be publicly transferred to Bob over the network. Apub=6
Bob: Bob will choose a random private number say Bpriv=13 Now Bob will have to do the same operation as of Alice
g^Bpriv mod p
3 mod 17=12 ??..eq2
Now the number 12 will be publicly transferred to Alice over the network.
Bpub=12
Alice:
Now Alice has the number publicly transmitted by Bob Bpub=12. She will decrypt the information using private key using the formula
Bpub^Apriv mod p = shared secret key
12? mod 17 = 10 ??..eq3
Bob:
Bob has to do the same process as Alice. Bob has the number publicly transmitted by Alice Apub=6 He will try to decrypt the information using his private key
Apub^Bpriv mod p = shared secret key
6 mod 17 = 10 ??..eq4
What happened? They used different numbers in their respective process but how come they obtain the same key?
Lets rewrite the equations
Alice Operations:
3? mod 17= 6 ??..eq112? mod 17 = 10 ??..eq3
Bob?s operations:
3 mod 17=12 ??..eq26 mod 17 = 10 ??..eq4
Lets again rewrite these equations in generic form:
Alice Operations:
g^Apriv mod p= Apub ??..eq1
Bpub^Apriv mod p = Key ??..eq3
Bob?s Operations:
g^Bpriv mod p= Bpub ??..eq2
Apub^Bpriv mod p = Key ??..eq4
What Bob did ?
from eq2 and eq3 we can substitute eq2 in eq3
(g^Bpriv mod p)^Apriv mod p = Keyi.e, g^Bpriv^Apriv mod p = Key
3?^ mod 17 = 10
What Alice did ?
from eq1 and eq4we can substitute eq1 in eq4
(g^Apriv mod p)^Bpriv mod p = Keyi.e, g^Apriv^Bpriv mod p = key
3^? mod 17 = 10
Using Property of Modular Exponent (Powers)(a^n)^m = a ^(n?m)
so3?^ mod 17 = 10 will be
3^(15×13) mod 17 = 10
3^? mod 17 = 10 will be
3^(13×15) mod 17 = 10
They do the same operation but in alternate order and end up with the same output.
Communication:
Now Alice and Bob have shared secret key obtained using Diffie Hellman Key Exchange algorithm. Since Alice and Bob transmitted their public info Apub and Bpub over the network. Any person say Eve who tries to steal the info will have Apub and Bpub but he cannot decrypt the information without knowing Alice and Bob private keys.
Important Point:
If we use small length numbers, anyone can compromise the key even using brute force attack within a second. In practice the key size used will be around 256 bits ? 4096 bits to maintain more secure communication.
Thank You!
