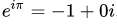Euler?s Identity
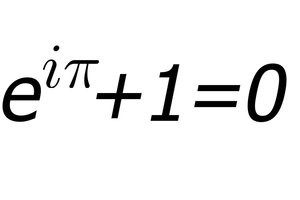
Euler?s Identity is written simply as: e^(i?) + 1 = 0, it comprises the five most important mathematical constants, and it is an equation that has been compared to a Shakespearean sonnet. The physicist Richard Feynman called it ?the most remarkable formula in mathematics?.
The Five important mathematical constants in Euler?s Identity:
The number ?0?: Zero is the only integer that is neither negative nor positive. It is also the only number that cannot be divided by itself.
The number ?1?: The number one is the smallest natural number, the factor of every number and is neither prime nor composite.
The imaginary number ?i?: An imaginary number denoted by the symbol ?i? , is a number that when squared is a negative number. The symbol ?i? is equal to the square root of -1: ?(-1). The imaginary number is not a real number in mathematics since no number can be multiplied by itself to produce a negative number, but there are situations where one needs to take the square root of a negative number like in electricity, more specifically alternating current (AC) electronics.
The number ??? (Pi): Pi is an irrational number meaning the digits never end. It is the ratio of the circumference of a circle to its diameter: (C/d), and is approximately 3.1415?
The number ?e?: The number ?e? also known as Euler’s constant shows up a lot in physics and math it is the base of the natural logarithms. The number ?e? is related to compound interest, it is the natural language of growth in general and so is used in Calculus.
The above is just a list of the important mathematical constants within Euler?s identity, there are many more important mathematical constants out there, like Pythagora?s constant also known as the square root of 2 or the Golden Ration. Euler?s identity implies that e^(i?) = -1 and was named after the mathematician Leonhard Euler. This identity is considered to be an example of beauty within mathematics that shows a amazing connection between some of the most fundamental numbers in math.
Deriving The Equation 1:
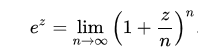
![]()
![]()
Deriving The Equation 2:
![]()
![]()
![]()
![]()
Thanks for reading this article I hope its helpful to you all ! Keep up the learning, and if you would like videos on computer science, programming and algorithm analysis videos please visit and subscribe to my YouTube channels (randerson112358 & compsci112358 )
RESOURCES:
https://www.livescience.com/51399-eulers-identity.htmlhttps://www.quora.com/Whats-so-special-about-the-Euler-number-ehttps://en.wikipedia.org/wiki/Euler%27s_identityhttps://en.wikipedia.org/wiki/Mathematical_constanthttps://www.wolframalpha.com/input/?i=limit+as+n+approaches+infinity+of+(1%2B(i*pi)+%2Fn)%5En