The Derivative of Cost Function for Logistic Regression

Introduction:

Linear regression uses Least Squared Error as a loss function that gives a convex loss function and then we can complete the optimization by finding its vertex as a global minimum. However for logistic regression, the hypothesis is changed, the Least Squared Error will result in a non-convex loss function with local minimums by calculating with the sigmoid function applied on raw model output.

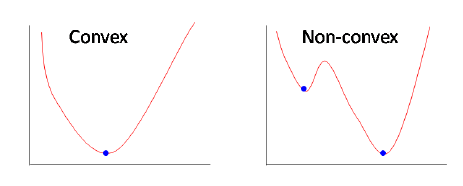Left(Linear Regression mean square loss), Right(Logistic regression mean square loss function)

However, we are very familiar with the gradient of the cost function of linear regression it has a very simplified form given below, But I wanted to mention a point here that gradient for the loss function of logistic regression also comes out to have the same form of terms in spite of having a complex log loss error function.

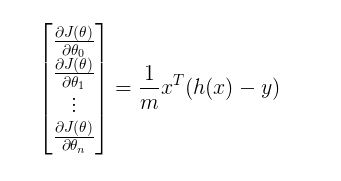Gradient for Linear Regression Loss Function

In order to preserve the convex nature for the loss function, a log loss error function has been designed for logistic regression. The cost function is split for two cases y=1 and y=0.

For the case when we have y=1 we can observe that when hypothesis function tends to 1 the error is minimized to zero and when it tends to 0 the error is maximum. This criterion exactly follows the criterion as we wanted

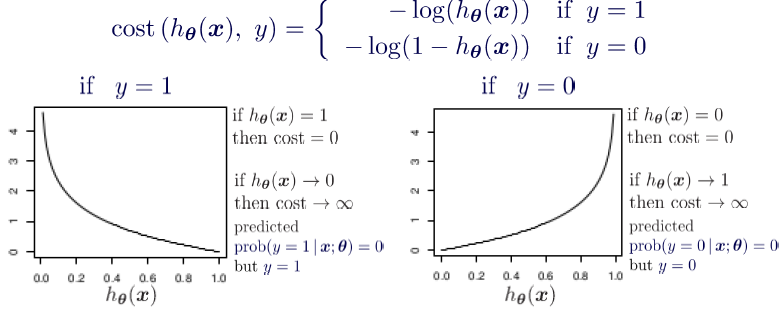Cost Function

Combining both the equation we get a convex log loss function as shown below-

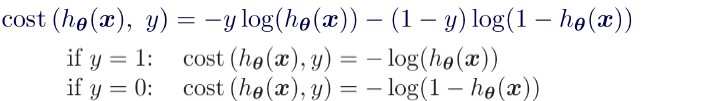Combined Cost Function

In order to optimize this convex function, we can either go with gradient-descent or newtons method. For both cases, we need to derive the gradient of this complex loss function. The mathematics for deriving gradient is shown in the steps given below

The Derivative of Cost Function:

Since the hypothesis function for logistic regression is sigmoid in nature hence, The First important step is finding the gradient of the sigmoid function. We can see from the derivation below that gradient of the sigmoid function follows a certain pattern.

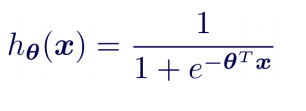Hypothesis Function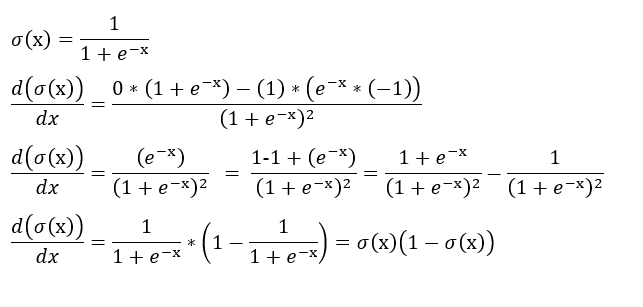Derivative of Sigmoid Function

Step 1:

Applying Chain rule and writing in terms of partial derivatives.

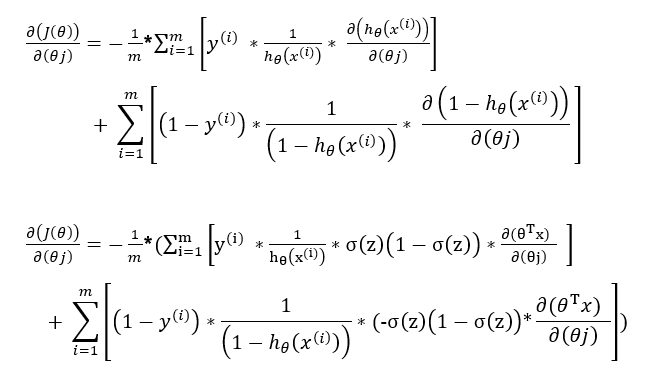
Step 2:

Evaluating the partial derivative using the pattern of the derivative of the sigmoid function.

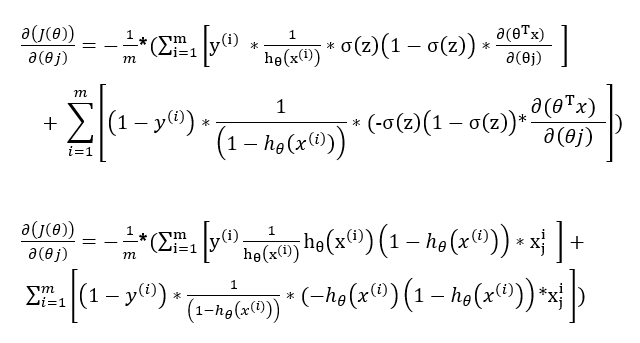
Step 3:

Simplifying the terms by multiplication

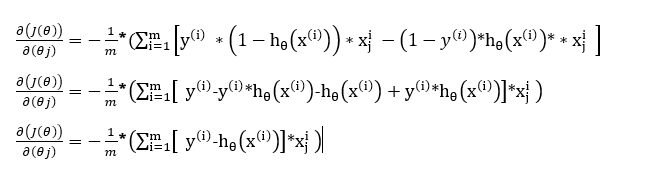
Step 4:

Removing the summation term by converting it into a matrix form for the gradient with respect to all the weights including the bias term.

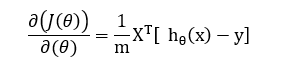
Conclusion:

This little calculus exercise shows that both linear regression and logistic regression (actually a kind of classification) arrive at the same update rule. What we should appreciate is that the design of the cost function is part of the reasons why such ?coincidence? happens.

Thank you for reading!!!!

If you like my work and want to support me:

1-The BEST way to support me is by following me on Medium.

2-Follow me on LinkedIn.