A high-level overview of how binary numbers make computers work for curious non-technical people.
 Photo by Federica Galli on Unsplash
Photo by Federica Galli on Unsplash
How computers work is something that I?ve always been curious about but never actually thought that I was going to have the actual basic knowledge to understand it, even at a high level. So doing the research to write this blog post and finding out that it wasn?t so hard to understand has been very rewarding, plus, getting to understand how computers work, again even at a high level, is pretty mind-blowing.
The most basic way of thinking of a computer is as an Input/Output machine. That?s a pretty basic idea: computers take information from external sources (your keyboard, mouse, sensors or the internet), store it, process it, and return the result (Output) of that process. By the way, if you think about it, the moment computers are connected through the internet there?s an ever ending loop of inputs and outputs as the output of a computer (say a website) becomes the input of another and so forth(!!).
Now, we are all pretty used and familiar with the ways a computer has to receive input and to print out some output, we?ve all used a mouse or a keyboard, or even talked to a computer and we?ve all read an article on a website, listened to music or browsed through some old pictures, etc. What we ain?t as familiar with, and what we usually struggle to understand is how a computer actually processes information.
So yes, on a very fundamental level all a computer understands is 1?s and 0?s which means that every single input and output gets at some point translated into or from 1?s and 0s. What is powerful about 1?s and 0?s (also called bits -from BInary digiT) is that it allows us to transform any information into electrical signals (ON/OFF). Please take a moment to think about it: ANYTHING you see, think or interact with can actually be translated and represented as electrical signals(!!!). Representing information as electrical signals is what allows computers to actually process that information and transform it.
So how does the binary number system works? Binary numbers mean that all numbers are computed with base 2. As an example, most of us are used to think of numbers with base 10. If you think about any number, let?s say 2561, you can see how depending on the position the number occupies from right to left, the number has a different value which is a multiple of ten. In this example, for instance, 1 occupies the 1s position, 6 occupies the 10s position, 5 occupies the 100s position and 2 occupies the 1000?s position. This way, (2×1000) + (5×100) + (6×10) + (1×1) = 2561. Binary numbers work in the exact same way but every incremental step represents an x2 increment over the previous one. Here?s an example of how to represent number 12:
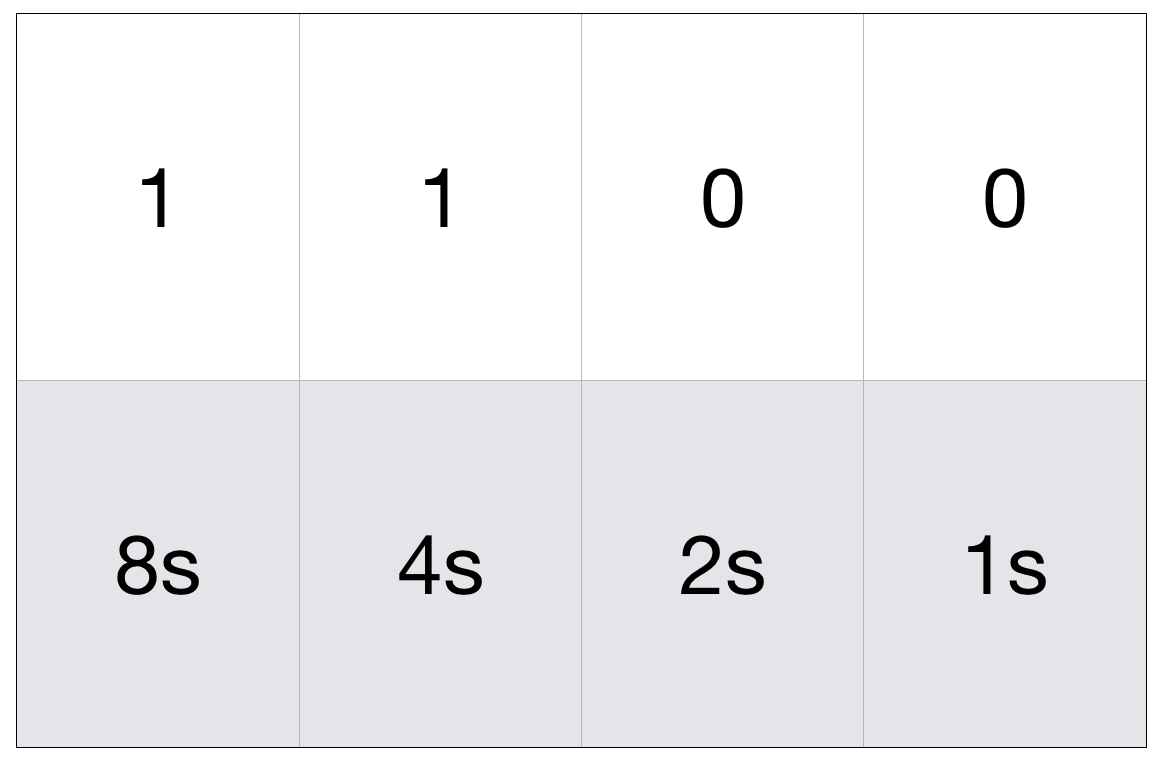
So, with 8 bits you can represent any number between 0 and 255, and with 32 bits you can represent any number between 0 and 4 billion. You might be thinking, sure but what about strings and punctuation? Well, as of today, we still follow the ASCII, American Standard Code for Information Interchange that basically maps any character or punctuation sign including capital letters to one of the 8-bit numbers. And this is how we use numbers to represent letters.
Sure, but what about images? Well, actually an image can also be reduced to 0?s and 1?s. As you know, any screen has a given number of pixels and every pixel has a color and as you know, using RGB or HEX color codes we can represent colors as numbers which means that we can basically tell a computer which color each pixel must have. The same thing goes for music, video and any other type of information you can think of.
But how the hell do we ?compute? electric signals? That is where electrical circuits come in. On a very basic and oversimplified level, we can use electrical circuits to behave as ?logical machines?. We can have circuits that, given a specific input, will return an output depending on the logic with which they?ve been built (Not, And, Or) but also sums, subtractions, multiplications, and divisions. The interesting part is that using these very elemental forms of representing and processing information we can actually achieve ?functional completeness? which is a term used in Logic to refer to a set of boolean operators which are able to represent all possible truth tables, which is a fancy way that mathematicians have to say that sky is the limit. All these calculations happen in a unit inside your CPU called ALU (Arithmetic Logic Unit).
As you probably know CPU?s ? Central Processing Unit ? are the brains of computers and it?s where all the computation happens. The interesting part about CPU?s is that they don?t have any memory which means that they can?t remember absolutely anything. Without memory, every computation would be lost right after we perform it. Roughly speaking, and as you might already know, there are two types of memory our computers use: RAM which stands for Random Access Memory and Persistent Memory. You can think of RAM memory as an immense grid (matrix) storing 8-bit numbers. RAM memory keeps track of the ?addresses? in the memory matrix of any given 8-bit number for whenever the CPU needs it. And guess what? In order to perform these operations, we use the exact same circuit logic that we used before. This is, we use the exact same logic to allow a given input to be stored in a given ?place? in the memory or to access whatever piece of information stored in it.
I know that I am barely scratching the surface of how computers work here, but just getting to understand this has taken me quite some time and has already blown my mind more than a few times. What fascinates me about this is how powerful computers are and how embedded they are in our everyday lives, this is why I think it?s important to at least have an intuition of how they work. Also, as always, if you spot any mistake please let me know.
I?ll finish this post with a video that I really like where Steve Jobs compares computers to bicycles here:
Here?s a list of amazing resources I?ve found while doing some research for this post:
Khan Academy?s 5 short videos on how computers work: https://www.khanacademy.org/computing/computer-science/how-computers-work2/v/khan-academy-and-codeorg-introducing-how-computers-work
Crash Course series on Computer Science are absolutely amazing: https://www.youtube.com/watch?v=O5nskjZ_GoI
An introduction to Logic and Truth Tables: https://medium.com/i-math/intro-to-truth-tables-boolean-algebra-73b331dd9b94
NAND Logic, to get a better understanding of how electrical circuits can perform logical operations: https://en.wikipedia.org/wiki/NAND_logic
The Wikipedia page for ASCII: https://en.wikipedia.org/wiki/ASCII
Wikipedia page for Binary Code with a short history of binary arithmetic: https://en.wikipedia.org/wiki/Binary_code
If you want to dig deeper, here?s a great place to start: https://softwareengineering.stackexchange.com/questions/81624/how-do-computers-work/81715
Thank you for reading so far.