First let?s talk what do you mean by optimising a model. Well simply we want the model to get trained to reach the state of maximum accuracy given resource constraints like time, computing power, memory etc. Optimization has a broad scope and you can also tweak the architecture to get a better model. But that is something which comes with intuition developed by experience.
Given a certain architecture, in pytorch a torch.optim package implements various optimization algorithms. We would discuss here two most widely used optimizing techniques stochastic gradient descent (optim.SGD) and Adam?s Method (optim.Adam).
- SGD:
We know that gradient descent is the rate of loss function w.r.t the weights a.k.a model parameters. The loss function can be a function of the mean square of the losses accumulated over the entire training dataset. Hence the weights are updated once at the end of each epoch. This results in reaching the exact minimum but requires heavy computation time/epochs to reach that point.
On the other hand in SGD the weights are updated after looping via each training sample.
for i in range(nb_epochs):np.random.shuffle(data) for example in data: params_grad = evaluate_gradient(loss_function, example, params) params = params – learning_rate * params_grad
From official documentation of pytorch SGD function has the following definition
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
Arguments:
- params (iterable) ? iterable of parameters to optimize or dicts defining parameter groups
- lr (float) ? learning rate
- momentum (float, optional) ? momentum factor (default: 0)
- weight_decay (float, optional) ? weight decay (L2 penalty) (default: 0)
- dampening (float, optional) ? dampening for momentum (default: 0)
- nesterov (bool, optional) ? enables Nesterov momentum (default: False)
Most of the arguments stated above I believe are self explanatory except momemtum and nesterov.
Stuck in a local minima
Nesterov Momentum
This type of momemtum has a slightly different methodology. Here weights update depend both on the classical momemtun and the gradient step in future with the present momemtum. The diagram below clearly depicts I?m trying to say.
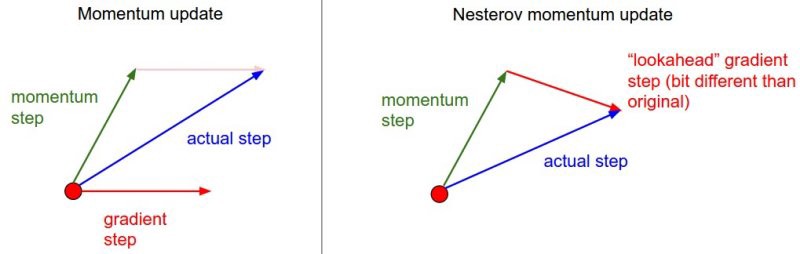x_ahead = x + mu * v# evaluate dx_ahead (the gradient at x_ahead instead of at x)v = mu * v – learning_rate * dx_aheadx += v
In fact it is said that SGD+Nesterov can be as good as Adam?s technique.
You can totally skip the details because in code you only need to pass values to the arguments. But it is good to know in dept of everything we want to learn.
2. Adam (Adaptive Momemt Estimation)
From the official documentation
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
Arguments:
- params (iterable) ? iterable of parameters to optimize or dicts defining parameter groups
- lr (float, optional) ? learning rate (default: 1e-3)
- betas (Tuple[float, float], optional) ? coefficients used for computing running averages of gradient and its square (default: (0.9, 0.999))
- eps (float, optional) ? term added to the denominator to improve numerical stability (default: 1e-8)
- weight_decay (float, optional) ? weight decay (L2 penalty) (default: 0)
- amsgrad (boolean, optional) ? whether to use the AMSGrad variant of this algorithm from the paper On the Convergence of Adam and Beyond (default: False)
Adam?s method considered as a method of Stochastic Optimization is a technique implementing adaptive learning rate. Whereas in normal SGD the learning rate has an equivalent type of effect for all the weights/parameters of the model.
Hm, let me show you the actual equations for Adam?s to give you an intuition of the adaptive learning rate per paramter.
m = beta1*m + (1-beta1)*dxmt = m / (1-beta1**t)v = beta2*v + (1-beta2)*(dx**2)vt = v / (1-beta2**t)x += – learning_rate * mt / (np.sqrt(vt) + eps)
We see that Adam somewhat implies two tricks one is momemtum
Another trick that Adam uses is to adaptively select a separate learning rate for each parameter. Parameters that would ordinarily receive smaller or less frequent updates receive larger updates with Adam (the reverse is also true). This speeds learning in cases where the appropriate learning rates vary across parameters. For example, in deep networks, gradients can become small at early layers, and it make sense to increase learning rates for the corresponding parameters. Another benefit to this approach is that, because learning rates are adjusted automatically, manual tuning becomes less important. Standard SGD requires careful tuning (and possibly online adjustment) of learning rates, but this less true with Adam and related methods. It?s still necessary to select hyperparameters, but performance is less sensitive to them than to SGD learning rates. ? Stackoverflow
I ?m writing this article myself as I?m diving deeper into deep learning fundamentals and concepts. Any suggestions on making the article better will be highly appreciated. I hope this article was of some help to you.
