Jupyter notebook is here.
History
Known to John von Neumann in 1945
Step 1- split
Given a list let?s split it into two lists right down the middle
def split(input_list): “”” Splits a list into two pieces :param input_list: list :return: left and right lists (list, list) “”” input_list_len = len(input_list) midpoint = input_list_len // 2 return input_list[:midpoint], input_list[midpoint:]
To help with our intuition here?s a list of inputs and expected outputs:
[ ({‘input_list’: [1, 2, 3]}, ([1], [2, 3])), ({‘input_list’: [1, 2, 3, 4]}, ([1, 2], [3, 4])), ({‘input_list’: [1, 2, 3, 4, 5]}, ([1, 2], [3, 4, 5])), ({‘input_list’: [1]}, (, [1])), ({‘input_list’: }, (, ))]
Every element in the list above consistent of a tuple. The first element of the tuple is the input and the second element is a tuple that contains the left and right sub-lists. For example the first input list is [1, 2, 3] and the output is [1] and [2, 3] for the left and the right sub-lists.
Step 2- merge sorted lists
Given two sorted lists we should be able to ?merge? them into a single list in a linear operation.
def merge_sorted_lists(list_left, list_right): “”” Merge two sorted lists This is a linear operation O(len(list_right) + len(list_right)) :param left_list: list :param right_list: list :return merged list “”” # Special case: one or both of lists are empty if len(list_left) == 0: return list_right elif len(list_right) == 0: return list_left # General case index_left = index_right = 0 list_merged = # list to build and return list_len_target = len(list_left) + len(list_right) while len(list_merged) < list_len_target: if list_left[index_left] <= list_right[index_right]: # Value on the left list is smaller (or equal so it should be selected) list_merged.append(list_left[index_left]) index_left += 1 else: # Right value bigger list_merged.append(list_right[index_right]) index_right += 1 # If we are at the end of one of the lists we can take a shortcut if index_right == len(list_right): # Reached the end of right # Append the remainder of left and break list_merged += list_left[index_left:] break elif index_left == len(list_left): # Reached the end of left # Append the remainder of right and break list_merged += list_right[index_right:] break return list_merged
A few test cases:
[ ({‘list_left’: [1, 5], ‘list_right’: [3, 4]}, [1, 3, 4, 5]), ({‘list_left’: [5], ‘list_right’: [1]}, [1, 5]), ({‘list_left’: , ‘list_right’: }, ), ({‘list_left’: [1, 2, 3, 5], ‘list_right’: [4]}, [1, 2, 3, 4, 5]), ({‘list_left’: [1, 2, 3], ‘list_right’: }, [1, 2, 3]), ({‘list_left’: [1], ‘list_right’: [1, 2, 3]}, [1, 1, 2, 3]), ({‘list_left’: [1, 1], ‘list_right’: [1, 1]}, [1, 1, 1, 1]), ({‘list_left’: [1, 1], ‘list_right’: [1, 2]}, [1, 1, 1, 2]), ({‘list_left’: [3, 3], ‘list_right’: [1, 4]}, [1, 3, 3, 4]),]
Step 3- merge sort
- Merge sort only needs to utilize the previous 2 functions
- We need to split the lists until they have a single element
- A list with a single element is sorted
- Now we can merge these single-element (or empty) lists
def merge_sort(input_list): if len(input_list) <= 1: return input_list else: left, right = split(input_list) # The following line is the most important piece in this whole thing return merge_sorted_lists(merge_sort(left), merge_sort(right))
A few simple test cases:
[ ({‘input_list’: [1, 2]}, [1, 2]), ({‘input_list’: [2, 1]}, [1, 2]), ({‘input_list’: }, ), ({‘input_list’: [1]}, [1]), ({‘input_list’: [5, 1, 1]}, [1, 1, 5]), ({‘input_list’: [9, 1, 10, 2]}, [1, 2, 9, 10]),]
Example walk through
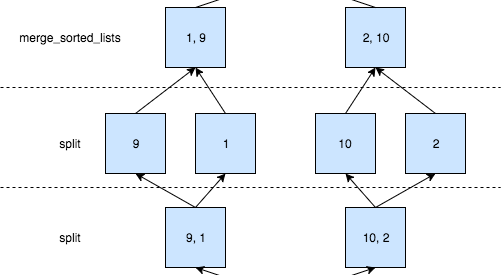
merge_sort keeps splitting until we get to single-element lists. Once we’re there (the base case of recursion) the callers can start applying merge_sorted_list. For the following example here’s what’s going on:
- input_list=[9, 1, 10, 2]
- left=[9, 1] and right=[10, 2]
- merge_sort([9, 1]) is responsible for sorting [9, 1], let’s call it L1.
- merge_sort([10, 2]) is reponsible for sorting [10, 2], let’s call it R1.
For L1:
- left=[9] and right=[1]
- merge_sort([9]) returns [9] since it’s the base case and merge_sort([1]) returns [1]
- merge_sorted_lists([9], [1]) returns [1, 9] which is sorted
Same thing happens for R1 and the result is [2, 10]. Now merge_sorted_lists(L1, R1) returns the final answer.
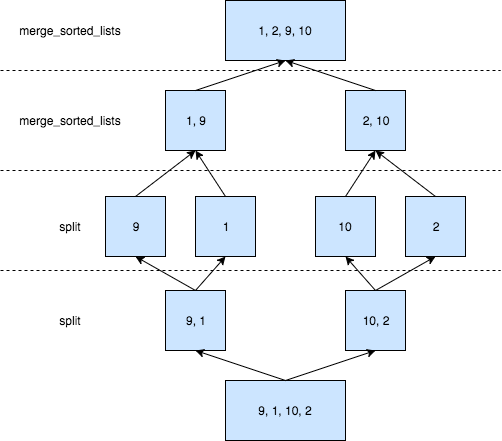Merge sort
Jupyter notebook is here.
