1. Definition of an orthogonal matrix
A ? ? ? square matrix ? is said to be an orthogonal matrix if its ? column and row vectors are orthogonal unit vectors. More specifically, when its column vectors have the length of one, and are pairwise orthogonal; likewise for the row vectors.
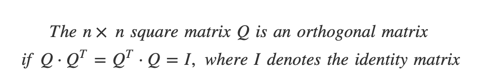
This leads to the following characterization that a matrix ? becomes orthogonal when its transpose is equal to its inverse matrix.
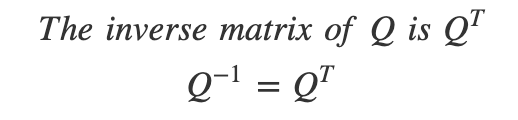
- Why the inverse matrix of ? is its transpose?
Figure 1. Proof that the inverse of ? is its transpose
2. Properties of orthogonal matrices
- 2.1 Any orthogonal matrix is invertible
- 2.2 The product of orthogonal matrices is also orthogonal
Figure 2. Proof that why the product of orthogonal matrices is orthogonal
- 2.3 The determinant of orthogonal matrices
The determinant of an orthogonal matrix is equal to 1 or -1. Since det(A) = det(A?) and the determinant of product is the product of determinants when A is an orthogonal matrix.
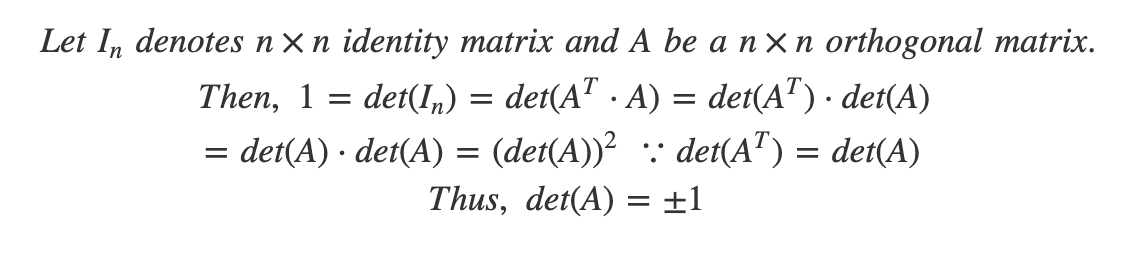Figure 3. Proof that why the determinant of an orthogonal matrix is 1 or -1
- 2.4 Preservation of lengths and angles
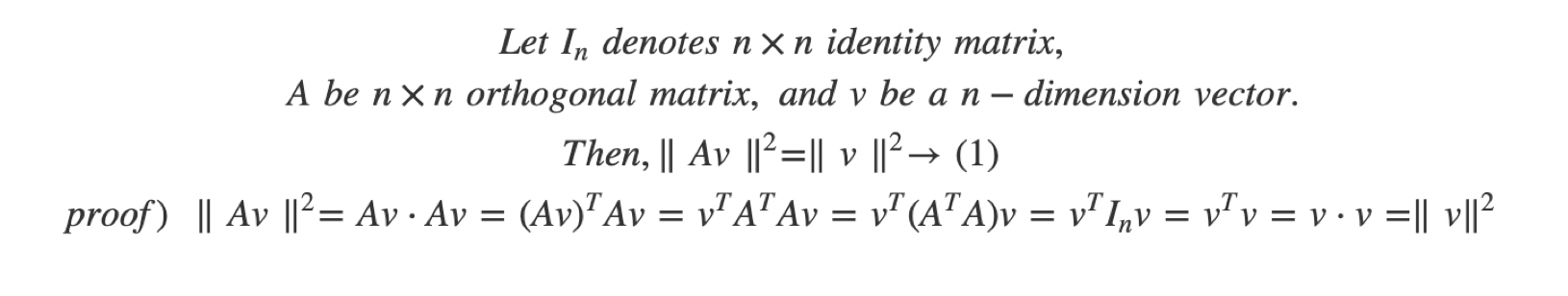Figure 4. Proof that why orthogonal matrices preserve lengths
Figure 5. Proof that why orthogonal matrices preserve angles
- 2.5 Orthogonal matrices represent a rotation
As is proved in the above figures, orthogonal transformation remains the lengths and angles unchanged. Also, its determinant is always 1 or -1 which implies the volume scaling factor. In other words, the orthogonal transformation leaves angles and lengths intact, and it does not change the volume of the parallelepiped. From these facts, we can infer that the orthogonal transformation actually means a rotation.
3. Reference
[1] https://en.wikipedia.org/wiki/Orthogonal_matrix
[2] https://www.quora.com/Why-do-orthogonal-matrices-represent-rotations
[3] https://byjus.com/maths/orthogonal-matrix/
[4]http://www.math.utk.edu/~freire/teaching/m251f10/m251s10orthogonal.pdf
[5] https://www.khanacademy.org/math/linear-algebra/alternate-bases/orthonormal-basis/v/lin-alg-orthogonal-matrices-preserve-angles-and-lengths
any corrections, suggestions, and comments are welcome
