With a Min-Heap

A common problem most programmers are probably familiar with is to merge two sorted arrays into a single sorted array. It?s actually one of the earliest problems we teach here at Outco during week 1. The approach is fairly straightforward and just involves using two pointers to find the next largest element between the two arrays, and adding that to the final result. The amount of time needed just depends on how many elements there are in the two arrays, and aside from the result array, you?ll only need two pointers to keep track of where you are in each array.
Input: [1, 3, 5, 7], [2, 4, 6, 8]Output: [1, 2, 3, 4, 5, 6, 7, 8]
But what if the number of arrays was variable? What if instead of two arrays, you could have 10, 20 or 100? Is there some way of extrapolating this approach and coming up with some general solution for an arbitrary number of arrays?
Input: [[1, 10, 11, 15], [2, 4, 9, 14], [5, 6, 8, 16], [3, 7, 12, 13]]Output: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]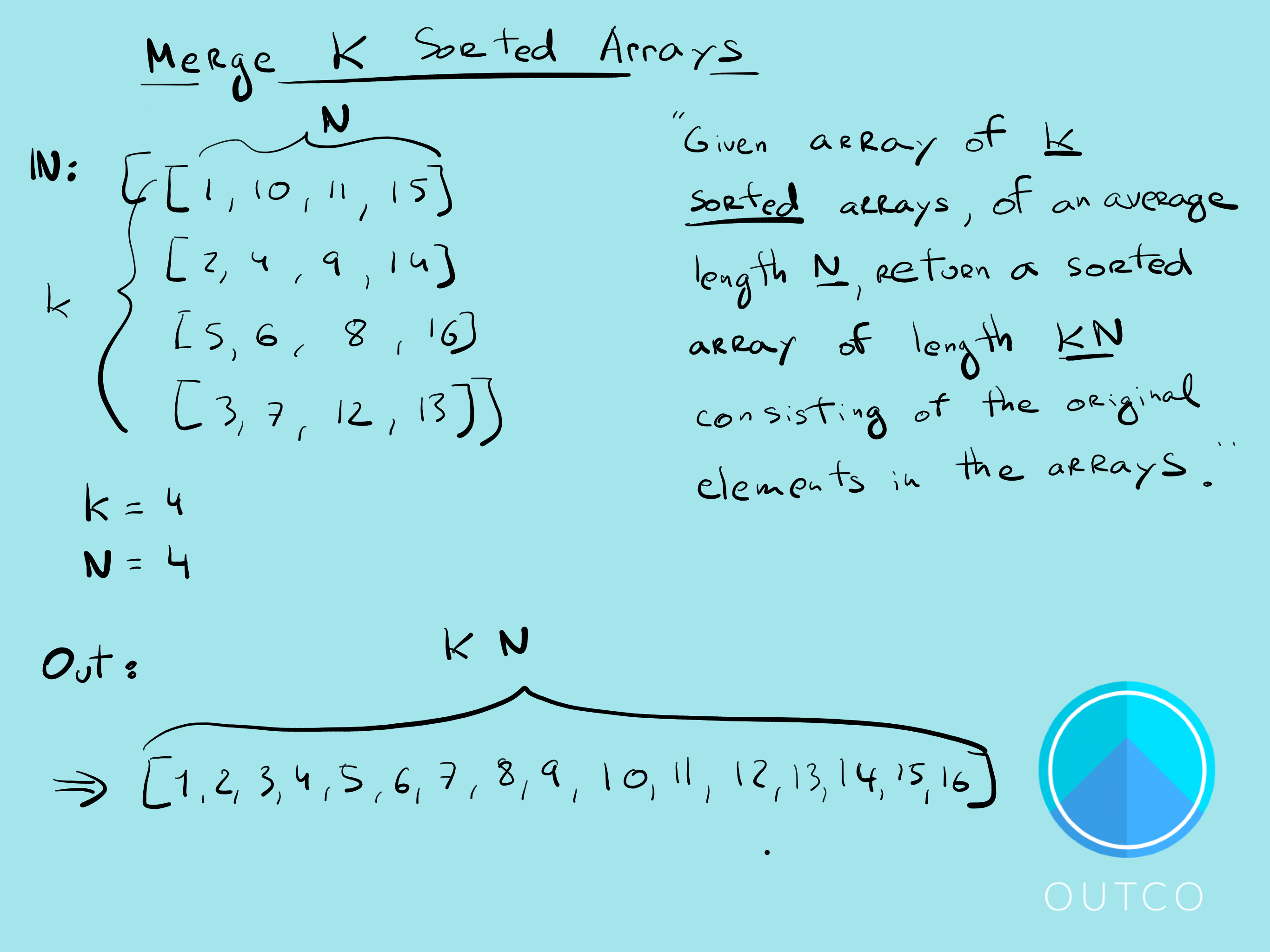
It turns out there is but we have to change our thinking about the problem a little. Two useful questions to ask are ?how does having a variable number of arrays change the problem?? and ?how does having more than two arrays change the problem??.
Knowing how many arrays you have from the outset is helpful because you?ll know exactly how many pointers you?ll need every time. For two arrays you can just hardcode in one pointer for each array. When the number of arrays varies, you?ll need a different way of keeping track of your pointers, probably in something like an array.
But there?s something else that happens when you have more than two arrays, that?s a bit more subtle. When you have two arrays, you?ll only ever have to perform one comparison per iteration to find the smaller of the two elements. However, this is just a special case and that constant-time comparison doesn?t scale. With three arrays, you?ll need to perform three comparisons to find the smallest element. With 4 arrays you?ll need to do 4 comparisons and so on.
After a certain number of arrays it becomes more efficient to just concatenate all the arrays together an apply an efficient sorting function on the result.
Time complexity of doing K comparisons each iteration:O(N * K * K)Time complexity of concatenating and sorting:O(N * K * log(N * K))
But concatenating and then sorting destroys any information you could have used about the arrays before when they were individually sorted, and though it?s more efficient, is still considered the naive approach. It is no different time-complexity-wise than it would be to merging and sorting K unsorted arrays.

Intuitively, you should be able to deduce that the arrays being sorted is helpful and that information can be used in some way.
It turns out the key to this problem is that you only ever need to know the current smallest element in all the arrays and have the ability to find the next smallest efficiently.
This is where heaps come into the equation.

A binary heap is similar to a binary search in that there is a relationship between parent and child nodes. The difference is in what that relationship is. In a BST right children are larger than their parents, and left children are smaller.
But in a binary min-heap, parent nodes are smaller than both their children, all nodes are inserted in breadth-first order, and there is no relationship between sibling nodes. The relationships can also be easily represented in an array as a mathematical formula between indices.
For a given index iIt’s two children will be at (2i + 1) and (2i + 2)So the children of the node at index 10 will be at 21 and 22.
If you aren?t very familiar with binary heaps I recommend brushing up on them here:
Binary Heap – GeeksforGeeks
A Binary Heap is a Binary Tree with following properties. 1) It’s a complete tree (All levels are completely filled?
www.geeksforgeeks.org
Array Representation Of Binary Heap – GeeksforGeeks
A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as array. The representation is done?
www.geeksforgeeks.org
HeapSort – GeeksforGeeks
Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort?
www.geeksforgeeks.org
They are super useful data structures when you need to maintain some kind of loose ordering and don?t want the overhead of sorting.
And it?s precisely that property of being almost sorted that makes them so useful. In fact, sorted arrays are a special kind of min-heap, but we don?t need our data structure to be that strict. At any point, we just need to have the next smallest element on hand. And heaps make that really simple:

Here?s my solution in 7 steps:



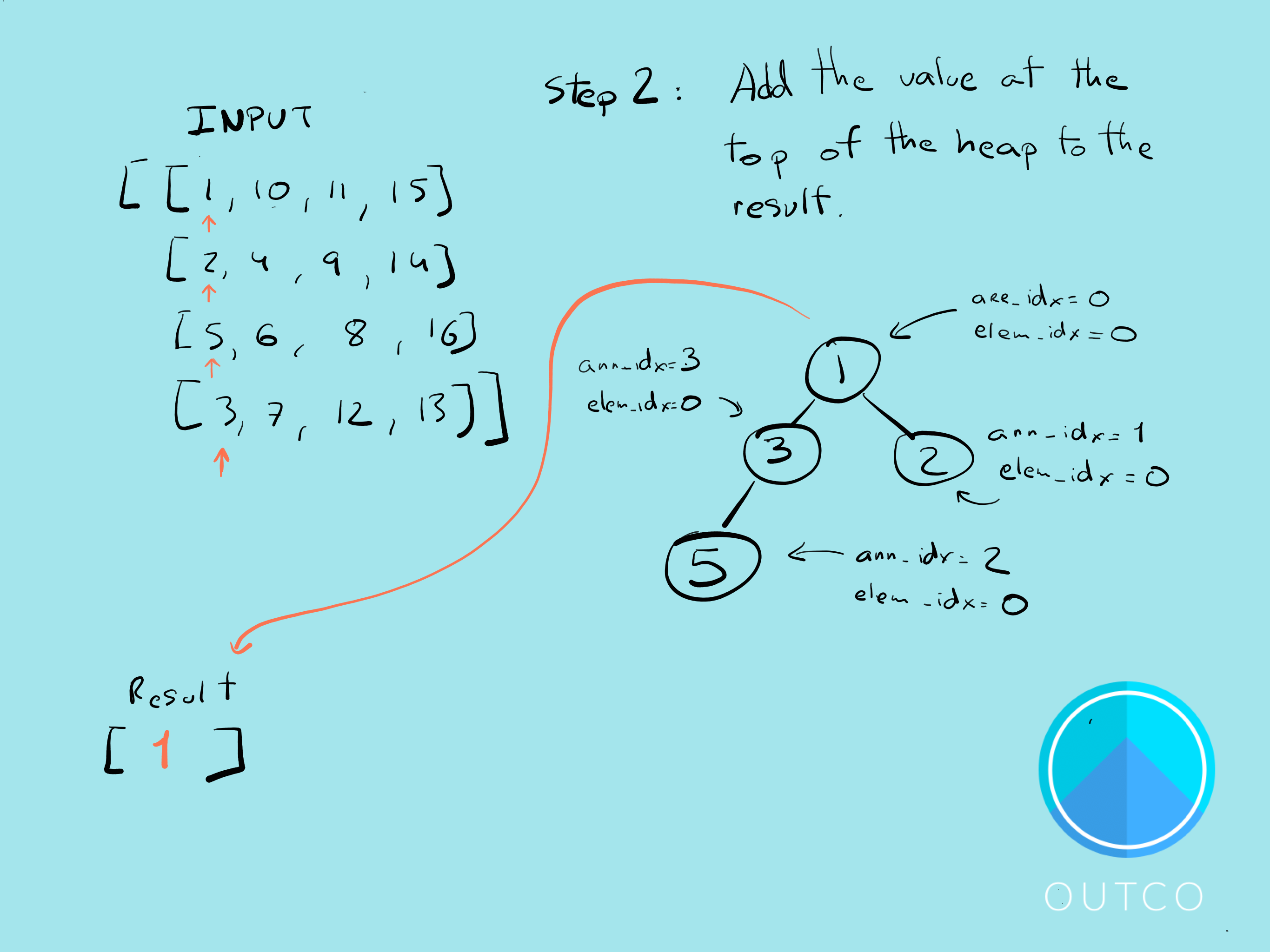



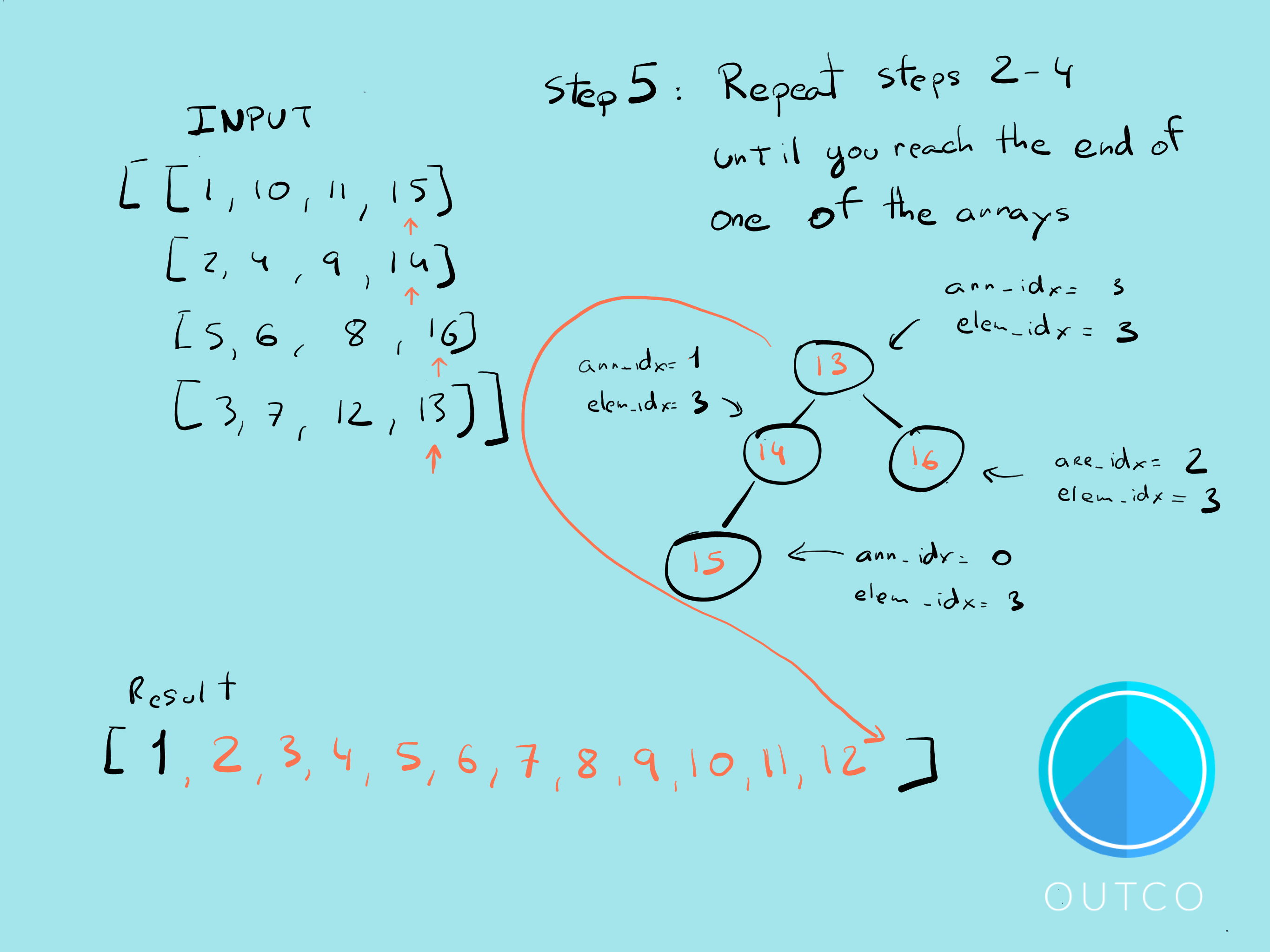




The code might seem a bit complex at first, but most of the methods build on one another pretty well. If you have a good understanding of heaps this problem should come naturally. And like I said earlier, heaps are incredibly useful data structures to understand.
Here?s a gist:
Hopefully you enjoyed this post, and if you?re interested in leveling up even more on algorithms and data structures be sure to check us out at Outco.io. In January we?ll have new classes starting twice a month!