How am I going to do this?

On November 1, 2016, I started a year-long project, challenging myself to master one expert-level skill every month. For the first eleven months, I succeeded at each of the challenges:

I landed a standing backflip, learned to draw realistic portraits, solved a Rubik?s Cube in 17 seconds, played a five-minute improvisational blues guitar solo, held a 30-minute conversation in a foreign language, built the software part of a self-driving car, developed musical perfect pitch, solved a Saturday New York Times crossword puzzle, memorized the order of a deck of cards in less than two minutes (the threshold to be considered a grandmaster of memory), completed one set of 40 pull-ups, and continuously freestyle rapped for 3 minutes.

Then, through a sequence of random events, I was offered the chance to sit down with the world chess champion Magnus Carlsen in Hamburg, Germany for an in-person chess game.

I accepted. How could I not?

And so, this became my twelfth and final challenge: With a little over one month of preparations, could I defeat world champion Magnus Carlsen at a game of chess?

Unlike my previous challenges, this one was near impossible.

I had selected all of my other challenges to be aggressively ambitious, but also optimistically feasible in a 30-day timespan. I set the challenges with the hope that I would succeed at 75% of them (I just wasn?t sure which 75%).

On the other hand, even if I had unlimited time, this challenge would still be dangerously difficult: The second best chess player in the world has a hard time defeating Magnus, and he?s devoted his entire life to the game. How could I possibly expect to have even a remote chance?

Truthfully, I didn?t. At least, I didn?t if I planned to learn chess like everybody else in the history of chess has.

But, this offered an interesting opportunity: Unlike my other challenges, where success was ambitiously in reach, could I take on a completely impossible challenge, and see if I could come up with a radical approach, rendering the challenge a little less impossible?

I wasn?t sure if I could, or not. But, I thought it would be fun to try.

I documented my entire process from start to finish through a series of daily blog posts, which are compiled here into a single narrative. In this article, you can relive my month of insights, frustrations, learning hacks, triumphs, and failures as I attempt the impossible.

At the end of this post, I share the video of the actual game against Magnus.

But first, let me walk you through how I prepared for the game, starting on October 1, 2017, when I had absolutely no plan. Just the desire to try.

Note: I was asked not to reveal the details of the actual game until after it happened and it was written about in the Wall Street Journal (the article is also linked at the end of this post). Thus, in order to document my journey via daily blog posts, without spoiling the game, I used the Play Magnus app for a bit of misdirection while framing up the narrative. However, I tried to write the posts so that, after the game happened and readers have knowledge of the match, the posts would still read naturally and normally.

Today, I begin the final month and challenge of my M2M project: Can I defeat world champion Magnus Carlsen at a game of chess?

The most immediate question is ?How will you actually be able to play Magnus Carlsen, #1-rated chess player in the world, at a game of chess??

Well, Magnus and his team have released an app called Play Magnus, which features a chess computer that is meant to simulate Magnus as an opponent. In fact, Magnus and team have digitally reconstructed Magnus?s playing style at every age from Age 5 until Age 26 (Magnus?s current age) by using records of his past games.

I will use the Play Magnus app to train, with the goal of defeating Magnus at his current age of 26. Specifically, I hope to do this while playing with the white pieces (which means I get to move first).

My starting point

My dad taught me the rules of chess when I was a kid, and we probably played a game or two per year when I was growing up.

Three years ago, during my senior year at Brown, I first downloaded the Play Magnus app and occasionally played against the computer with limited success.

In the past year, I?ve played a handful of casual games with equally-amateurish friends.

In other words, I?ve played chess before, but I?m definitely not a competitive player, nor do I have any idea what my chess rating would be (chess players are given numeric ratings based on their performance against other players).

This morning, I played five games against the Play Magnus app, winning against Magnus Age 7, winning and losing against Magnus Age 7.5, and winning and losing against Magnus Age 8.

Then, tonight, I filmed a few more games, winning against Magnus 7, Magnus 7.5, and Magnus 8 in a row, and then losing to Magnus 9. (There?s no 8.5 level).

It seems that my current level is somewhere around Magnus Age 8 or Age 9, which is clearly quite far from Magnus 26.

As reference, Magnus became a grandmaster at Age 13.

An extra week

While every challenge of my M2M project has lasted for exactly a month, this challenge is going to be slightly different ? although not by much. Rather than ending on October 31, I will be ending this challenge on November 9 (Updated to November 17).

I?d prefer to keep this challenge strictly contained within the month of October, but I think it?s going to be worth bending the format slightly.

Later in the month, I?ll explain why I?ve decided to adjust the format. For now, I can?t say much more.

If anything, I can use the extra training time, especially since this challenge is likely my most ambitious.

Anyway, tomorrow, I?ll start trying to figure out how I?m going to pull this off.

Yesterday, to test my current chess abilities, I played a few games against the Play Magnus app at different age levels (from Age 7 to Age 9).

While these games gave me a rough sense of my starting point, they don?t give me a clear, quantitative way to track my day-over-day progress. Thus, today, I decided to try and compute my numeric chess rating.

As I mentioned yesterday, chess players are given numeric ratings based on their performance against other players. The idea is that, given two players with known ratings, the outcome of a match should be probabilistically predictable.

For example, using the most popular rating system, called Elo, a player whose rating is 100 points greater than their opponent?s is expected to win 64% of their matches. If the difference is 200 points, then the stronger player is expected to win 76% of matches.

With each win or loss in a match, a player?s rating is updated, based on the following (semi-arbitrary, but agreed upon) Elo equation:

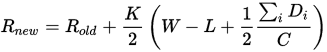Rnew and Rold are the player?s new and old rating respectively, Di is the opponent?s rating minus the player?s rating, W is the number of wins, L is the number of losses, C = 200 and K = 32.

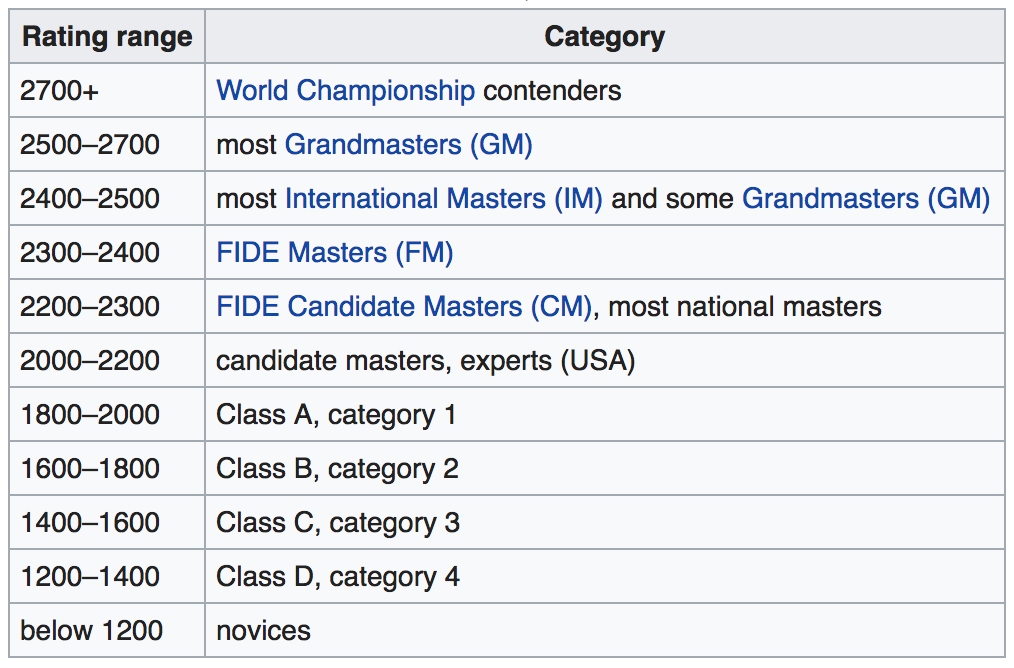
More interestingly, here?s how particular ratings correspond to categories of players (according to Wikipedia). Notably, a grandmaster has a rating around 2500 and a novice is below 1200.

Additionally, according to the United States Chess Federation, a beginner is usually around 800, a mid-level player is around 1600, and a professional, around 2400.

Magnus is currently rated at 2826, and has achieved the highest rating ever at 2882 in May 2014.

My current rating is somewhere around 1100, putting me squarely in the novice category. To determine this rating, I played a number of games today on Chess.com, which maintains and computes ratings for all the players on the site.

Chess.com is actually really cool: At the click of a button, you are instantly matched with another chess player of similar skill level from anywhere in the world.

Chess.com doesn?t use the Elo rating system, but, according to the forums, my Chess.com rating should be roughly equal to my Elo rating. In other words, I?m definitely an amateur.

So, over the next month, I just need to figure out how to boost my rating from 1100 to 2700?2800.

I?m still not sure exactly how to do this, or if it?s even possible (I?m almost certain no one has even made this kind of jump even in the span of five years), but I?m going to give it my best shot.

The good news about starting in amateur territory is there?s really only one direction to go?

Doesn?t this seem like a bad way to finish your project?? says most of my friends when discussing this month?s challenge. ?It seems like it?s effectively impossible. Isn?t it anticlimactic if you fail on the last challenge, especially after eleven months of only successes??

These friend do have a point: This month?s challenge (defeating Magnus Carlsen at a game of chess) is dancing on the boundary between what?s possible and what?s not.

However, for this exact reason, I see this month as the best possible way to finish off this project. Let me explain?

There are two ways you can live your life: 1. Always succeeding by playing exclusively in your comfort zone and shying away from the boundary of your personal limits, or 2. Aggressively pursuing and finding your personal limits by hitting them head on, resulting in what may be perceived as ?failure?.

In fact, failure is the best possible signal, as it is the only way to truly identify your limits. So, if you want to become the best version of yourself, you should want to hit the point of failure.

Thus, my hope with this project was to pick ambitious goals that rubbed right up against this failure point, pushing me to grow and discover the outer limits of my abilities.

In this way, I failed: My ?successful? track record means that I didn?t pick ambitious enough goals, and that I left some amount of personal growth on the table.

In fact, most of the time, when I completed my goal for the month, I was weirdly disappointed. For example, here?s a video where I land my very first backflip and then try to convince my coach that it doesn?t count.

In other words, my drug of choice is the constant, day-over-day pursuit of mastery, not the discrete moment in time when a particular goal is reached. As a result, I can maximize the amount of this drug I get to enjoy by taking my pursuits all the way to the boundary of my abilities and to the point of failure.

Therefore, while this month?s challenge is a bit far-fetched, it?s the realest embodiment of what this project is all about. By attempting to defeat Magnus as my last challenge, I hope to fully embrace the idea that failure is the purest signal of personal growth.

Now, with that said, I?m going to do everything I possibly can to beat Magnus. I?m not planning for failure. I?m playing for the win.

But, I do understand what I?m up against: Even the second best chess player in the world struggles to win against Magnus.

So for me, it isn?t about winning or losing, but instead, it?s about the pursuit of the win. It?s about the fight.

The outcome doesn?t dictate success. The quality of the fight does.

And this month, I?m set up for the best and biggest fight of the entire year.

In the past few days, I?ve played many games of chess on Chess.com and spent a lot of time researching the game, approaches to learning, etc. The hope is that I can find some new insight that will enable me to greatly accelerate my learning speed.

So far, I?ve yet to find this insight.

Chess is a particularly hard game ?to fake? because, in almost all cases, the better player is simply the one who has more information.

In fact, in a famous study by Adriaan de Groot, it was shown that expert chess players and weaker players look forward or compute lines approximately the same number of moves ahead, and that these players evaluate different positions, to a similar depth of moves, in roughly similar speeds.

In other words, via this finding, de Groot suggests that an expert?s advantage does not come from her ability to perform brute force calculations, but instead, from her body of chess knowledge. (While it has since been shown that some of de Groot?s claims aren?t as strong as originally thought, this general conclusion has held up).

In this way, chess expertise is mostly a function of the expert?s ability to identify, often at a glance, a huge corpus of chess positions and recall or derive the best move in each of these positions.

Thus, if I choose to train in traditional way, I would essentially need to find some magical way to learn and internalize as many chess positions as Magnus has in his over 20 years of playing chess. And this is why this month?s challenge seems a bit far-fetched.

But, what if I didn?t rely on a large knowledge base? What if I instead tried to create a set of heuristics that I could use to evaluate theoretically any chess position?

After all, this is how computers play chess (via positional computation), and they are much better than humans.

Could I invent a system that let?s me compute like a computer, but that can work with the processing speeds of my human brain?

There?s a 0% chance that I?m the first person to consider this kind of approach, so maybe not. But, there?s a lot of data out there (i.e. I have downloaded records of every competitive chess match Magnus has ever played), so perhaps something can be worked out.

Clearly, I can?t play by the normal chess rules if I want any shot of competing at the level of Magnus. (By ?normal chess rules? I mean the normal way people learn chess. If I could just bend the actual rules of the game, i.e. cheating, then this challenge would definitely be easier?).

I?m skeptical that some magical analytical chess method exists, but it?s worth thinking about it for a few days, and seeing if I can make any progress.

Hopefully, soon, I?ll be able to formulate an actual training approach for this month. Right now, I?m still floating around in the discovery phase.

As soon as I have an interesting training idea, I?ll be sure to share it.

Yesterday, I wondered if I could sidestep the traditional approach to learning chess, and instead, develop a chessboard evaluation algorithm that I could perform in my head, effectively transforming me into a slow chess computer.

Today, I?ve thought through how I might do this, and will use this post as the first of a few posts to explore these ideas:

Method 1: The extreme memory challenge

Chess has a finite number of states, which means that the 32 chess pieces can only be arranged on the 64 squares in so many different ways.

Not only that, but for each of these states, there exists an associated best move.

Therefore, theoretically, I can become the best chess player in the world entirely through brute force, simply memorizing all possible pairs of chessboard configurations and associated best moves.

In fact, I already have an advantage: Back in November 2016, I became a grandmaster of memory, memorizing a shuffled deck of playing cards in one minute and 47 seconds. I can simply use the same mnemonic techniques to memorize all chessboard configurations.

If I wanted to be smart about it, I could even rank chessboard configurations by popularity (based on records of chess matches) or likelihood (based on the number of ways the configuration can be reached). By doing so, I can start by memorizing all the most popular chessboard configurations, and then, proceed toward the least likely ones.

This way, if I run out of time, at least I?ll have memorized the most useful pairs of configurations and best moves.

But, this ?running out of time? problem turns out to be a very big problem?

It?s estimated that there are on the order of 10? possible chessboard configurations. So, even if I could memorize one configuration every second, it would still take me slightly less than one trillion trillion trillion years (3.17 10? years) to memorize all possible configurations.

I?m trying to contain this challenge to about a month, so this is pushing it a bit.

Also, if I had one trillion trillion trillion years to spare, I might as well learn chess the traditional way. It would be much faster.

Method 2: Do it like a computer

Even computers don?t have the horsepower to use the brute force approach. Instead, they need to use a set of algorithms that attempt to approximate the brute force approach, but in much less time.

Here?s generally how a chess computer works?

For any given chessboard configuration, the chess computer will play every possible legal move, resulting in a number of new configurations. Then, for each of these new configurations, the computer will play every legal move again, and so on, branching into all the possible future states of the chessboard.

At some point, the computer will stop branching and will evaluate each of the resulting chessboards. During this evaluation, the computer uses an algorithm to compute the relative winning chances of white compared to black based on the particular board configuration.

Then, the computer takes all of these results back up the tree, and determines which first order move produced the most future states with strong relative winning chances.

Finally, the computer plays this best move in the actual game.

In other words, the computer?s strength is based on 1. How deep the computer travels in the tree, and 2. How accurate the computer?s evaluation algorithm is.

Interestingly, essentially all chess computers optimize for depth, and not evaluation. In particular, the makers of chess computers will try to design evaluation algorithms that are ?good enough?, but really fast.

By having an extremely fast evaluation algorithm, the chess program can handle many more chess configurations, and thus, can explore many more levels of the tree, which grows exponentially in size level by level.

So, if I wanted to exactly replicate a chess computer, but in my brain, I would need to be able to extrapolate out to, remember, and quickly evaluate thousands of chessboard configurations every time I wanted to make a move.

Because, for these kinds of calculations, I?m much slower than a computer, I again would simply run out of time. Not in the game. Not in the month. But in my lifetime many times over.

Thus, unlike computers, I can?t rely on depth ? which leaves only one option: Learn to compute evaluation algorithms in my head.

In other words, can I learn to perform an evaluation algorithm in my head, and, if I can, can this algorithm be effective without going past the first level of the tree?

The answer to the second question is yes: Recently, using deep learning, researchers have built effective chess computers that only evaluate one level deep and perform just as well as the best chess computers in the world (although they are about 10x slower).

Perhaps, I can figure out how to convert this evaluation algorithm into something that I can computational perform in my head a la some kind of elaborate mental math trick.

I have some ideas about how to do this, but I need to experiment a bit further before sharing. Hopefully, by tomorrow, I?ll have something to share.

Yesterday, I determined that my best chance of defeating Magnus is learning how to numerical compute chessboard evaluations in my head. Today, I will begin to describe how I plan to do this.

How a deep learning-based chess computer works

It?s probably useful to understand how a computer uses deep learning to evaluate chess positions, so let?s start here?

Bitboard representation

The first step is to convert the physical chessboard position into to a numerical representation that can be mathematically manipulated.

In every academic paper I?ve read, the chessboard is converted into its bitboard representation, which is a binary string of size 773. In other words, the chessboard is represented as a string of 773 1?s and 0’s.

Why 773?

Well, there are 64 squares on a chessboard. For each square, we want to encode which chess piece, if any, is on that square. There are 6 different chess piece types of 2 different colors. Therefore, we need 64 x 6 x 2 = 768 bits to represent the entire chess board. We then use five more bits to represent the side to move (one bit, representing White or Black) and the castling rights (four bits for White?s kingside, White?s queenside, Black?s kingside, and Black?s queenside).

Thus, we need 773 binary bits to represent a chessboard.

The simple evaluation algorithm

Once the chessboard is converted into its numerical form (which we will denote as the vector x), we want to perform some function on x, called f(x), so that we get a scalar (single number) output y that best approximates the winning chances of white (i.e. the evaluation of the board). Of course, y can be a negative number, signifying that the position is better for black.

The simplest version of this function y = f(x) would be y = wx, where w is a vector of 773 weights that, when multiplied with the bitboard vector, results in a single number (which is effectively some weighted average of each of the bitboard bits).

This may be a bit confusing, so let?s understand what this function means for actual chess pieces on an actual chessboard?

This function is basically saying ?If a white queen is on square d4 of a chessboard, then add or subtract some corresponding amount from the total evaluation score. If a black king is on square c2, then add or subtract some other corresponding amount from the total evaluation score? and so on for all permutations of piece types of both colors and squares on the chessboard.

By the way, I haven?t mentioned it yet, so now is a good time to do so: On an actual chessboard, each square can be referred to by a letter from a to h and a number from 1 to 8. This is called algebraic chess notation. It?s not super important to fully understand how this notation is used right now, but this is what I mean by ?d4? and ?c2? above.

Anyway, this evaluation function, as described above, is clearly too crude to correctly approximate the true evaluation function (The true evaluation function is the just the functional form of the brute force approach. Yesterday, we determined this approach to be impossible for both computers and humans).

So, we need something a little bit more sophisticated.

The deep learning approach

Our function from above mapped the input bits from the bitboard representation directly to a final evaluation, which ends up being too simple.

But, we can create a more sophisticated function by adding a hidden layer in between the input x and the output y. Let?s call this hidden layer h.

So now, we have two functions: One function, f(x) = h, that maps the input bitboard representation to an intermediate vector called h (which can theoretically be of any size), and a second function, f(h) = y, that maps the vector h to the output evaluation y.

If this is not sophisticated enough, we can keep adding more intermediate vectors, h, h, h, etc., and the functions that map from intermediate step to intermediate step, until it is. Each intermediate step is called a layer and, the more layers we have, the deeper our neural network is. This is where the term ?deep learning? comes from.

In some of the papers I read, the evaluation functions only had three layers, and in other papers, the evaluation function had nine layers.

Obviously, the more layers, the more computations, but also, the more accurate the evaluation (theoretically).

Number of mathematical operations.

Interestingly, even though these evaluation functions are sophisticated, the underlying mathematical operations are very simple, only requiring addition and multiplication. These are both operations that I can perform in my head, at scale, which I?ll discuss in much greater depth in the next couple of days.

However, even if the operations themselves are simple, I would still need to perform thousands of operations to execute these evaluation functions in my brain, which could still take a lot of time.

Let?s figure just how many operations I would need to perform, and just how long that would take me.

Again, suspend your disbelief about my ability to perform and keep track of all these operations. I?ll explain how I plan to do this soon.

How much computation is required?

Counting the operations

Let?s say that I have an evaluation function that contains only one hidden layer, which has a width of 2048. This means that the function from inputs x to the internal vector h, f(x) = h, converts a 773-digit vector into a 2048-digit vector, by multiply x by a matrix of size 773 x 2048. Let?s call this matrix W. (By the way, I picked this setup because the chess computer, Deep Pink, uses intermediate layers of size 2048).

To execute f in this way requires 773 x 2048 = 1,583,104 multiplications and (773?1) x 2048 = 1,581,056 additions, totaling to 3,164,160 operations.

Then, f converts h to the output scalar y, by multiplying h by a 2048-digit vector, called w, which requires 2048 multiplications and 2047 additions, or 4095 total operations.

Thus, this evaluation function would require that I perform 3,168,255 total operations.

Counting the memory capacity required

To perform this mental calculation, not only will I need to execute these operations, but I?ll also need to have enough memory capacity.

In particular, I?ll have needed to pre-memorize all the values of matrix W, which is 1,583,104 numbers, and vector w, which is 2048 numbers. I would also need to remember h while computing f, so I can use the result to compute f, which requires that I remember another 2048 numbers.

Let?s now convert this memorization effort to specific memory operations.

For the 1,583,104 weights of W and the 2048 weights of w, I would only require a read operation from my memory for each (during game-time computation).

For the 2048 digits of h, I would require both a write operation and a read operation for each.

Thus, I would require 1,587,200 read operations and 2048 write operations, or 1,589,248 in total.

How long would this take?

We now know that I would need to execute 3,168,255 mathematical operations and 1,589,248 memory operations to evaluation a given chess position. How long exactly would this take?

This of course depends on the size of the multiplication and divisions, and the sizes of the numbers being stored in memory. I?ll talk more about this sizing soon, but for now, I?ll just provide my estimates.

I estimate that I could perform one mathematical operation in 3 seconds and one memory operation in 1 second. Thus, I could evaluate one chess position in 11,094,013 seconds or a little over four months.

Clearly, this is a long time (and doesn?t factor in the fact that I can?t, as a human, process continuously for 4 months), but we?re getting closer.

Of course, in a given chess game, I would need to make more than one evaluation. Since I?m a pretty novice player, I estimate that I would need to evaluate ~10?15 options per move.

Since the average chess game is estimated to be 40 moves, this would be about 500 evaluations per game.

Therefore, to play an entire chess game using this method, I would need 2,000 months or 167 years to play the game.

Of course, this is still problematic, but way less problematic than yesterday?s conclusion of one trillion trillion trillion years. In fact, I?m getting closer to an approach that I could actually execute in my lifetime (let?s say I have 75 years left to live).

The next step

I?ve made two assumptions above, one of which is good news for me and one of which is bad news for me.

First, the bad news: It would take me 167 years to play one chess game, assuming that my one-level deep evaluation function was sufficiently good. I suspect that one level isn?t enough, and that at least two or three levels would be needed, if not more.

The good news is that I?m not a computer, which means there is no reason I need to use bitboard representation as my starting point, potentially allowing me to reduce the size of the problem substantially.

Computers like 1?s and 0?s, and don?t care too much about ?big numbers? like 773, which is why bitboard representation is optimal for computers.

But, for me, I can deal with any two- or three-digit number just as well as I can deal with a 1 or 0 from a memory perspective and almost as well as I can from a computational perspective.

I think I could squash my chessboard representation to under 40 digits, which would significantly reduce the number of operations necessary (although, may slightly increase the operation time).

In the next few days, I?ll discuss how I plan to reduce the size of the problem and optimize the evaluation function for my human brain, so that I can perform all the necessary evaluations in a reasonable timeframe.

Last night, I climbed into bed, ready to go to sleep. As soon as I closed my eyes, I realized that I made a major mistake in my calculations from yesterday.

Well, technically I didn?t make a mistake. The chessboard evaluation algorithm I described yesterday does require 3,168,255 math operations and 1,589,248 memory operations. However, I failed to recognize that most of these operations are irrelevant.

Let me explain?

If you haven?t yet read yesterday?s post, it would be very helpful for you to read that first. Read it here.

Addressing my mistake

Yesterday, I introduced bitboard representation, which is a way to completely describe the state of a chessboard via 773 1?s and 0?s. Bitboard representation is the input vector to my evaluation function.

When calculating the number of math operations this evaluation function would require, I overlooked the fact that only a maximum of 37 digits out of the 773 in bitboard representation can be 1?s, and the rest are 0?s.

This is important for two reason:

1. The function, f(x), that converts the input bitboard representation x into the hidden vector h, doesn?t actually require any multiplication operations, since either I?m multiplying by 0 (in which case, the term can be completely ignored), or I?m multiplying by 1 (in which case, the original term can be used unchanged). In this way, all 1,583,104 multiplication operations that I estimated yesterday are no longer necessary.
2. f(x) only requires addition operations between all the 1?s in the bitboard representation, which we?ve now correctly capped at 37. Therefore, instead of 1,581,056 addition operation as estimated yesterday, the algorithm only requires 36 x 2048 = 73,728 operations.

f still requires the same 4095 operations, which means that, in total, the evaluation algorithm only requires 77,823 math operations.

This is a 40x improvement from yesterday.

Additionally, the memory operations scale down in the same way: For f, I only need (37 x 2048) + 2048 =77,824 read operations, and 2048 write operations, totaling to 79,872 memory operations.

Therefore, in total, the evaluation algorithm described yesterday actually only requires 157,695 total operations.

Computing the new time requirements

If I again assume that I can perform one mathematical operation in 3 seconds and one memory operation in 1 second, I would be able to evaluate one chess position in 313,341 seconds or 3.6 days, which is down considerably from yesterday?s four months.

Still, if we assume that I would need to execute 500 evaluations per game, I would need 3.6 days x 500 evaluations = 5 years to play one game.

5 years is still too long, but at least now I can complete one game of (computationally beautiful) chess in my lifetime.

But, I think I can do better?

Using ?Threshold Search?

Yesterday, I assumed that I would need to evaluate 10?15 options per move in order to find the optimal option. In other words, I would perform 15 evaluations, determine which move led to the greatest evaluation score, and then play that move in the game.

However, what if it?s unnecessary to find the absolute best move? What if it?s only necessary to find a move with an evaluation above a certain threshold?

Then, for a given move, I can stop evaluating once I find the first board position that surpasses this threshold. Theoretically, I could pick this board position on my first try (although, I wouldn?t be able to do this consistently. Otherwise, I would just be the world?s greatest chess player).

Though, I estimate I could find a threshold-passing move in 2.5 evaluations on average.

Therefore, if I?m able to implement this thresholding into my evaluation algorithm, I can reduce the number of evaluations from 500 to 100.

But, I can still do better?

Playing the opening

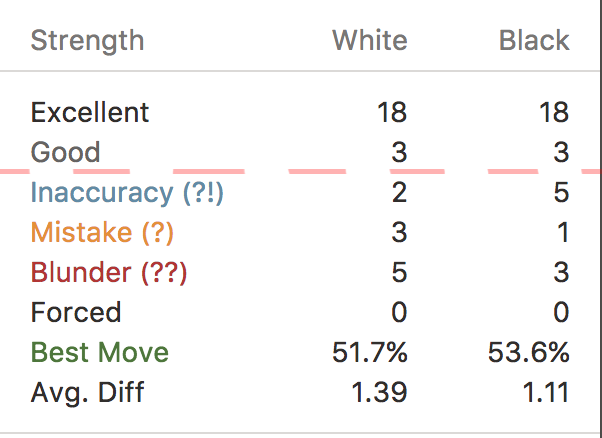
On Chess.com, I?m able to run my games through a real chess computer that analyzes each of my moves. The computer categorizes the moves into ?Excellent? (for when I play the absolute best move), ?Good? (for when I play a move above the threshold, but not the best move), and ?Inaccuracy?, ?Mistake?, and ?Blunder? (for when I screw up).

You?ll notice that 8 out of my 49 moves were below the threshold (I was playing White).

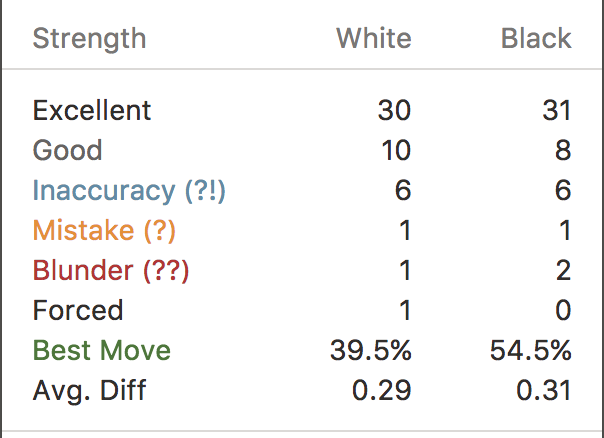
Interestingly though, going through all of my games, I seem to play moves exclusively in the Excellent and Good categories until about move 12?15, at which point, the game becomes too complex and I?m in trouble.

I?ve also found that towards the end of the game, I make very few below-threshold moves.

Based on this data, let?s say that I only need to perform my mental evaluations for 24 out of the 40 moves found in an average game.

Thus, in one game, I?d only require 60 total evaluations, and at 3.6 days per evaluation, I could complete a full game in 7 months.

This is getting closer, but I can still do better?

Finding reductions via ?Update Operations?

Right now, every time I?m doing an evaluation, I?m starting the computation over from scratch, which isn?t actually necessary, and far from most efficient.

Particularly, the hidden layer h, the output of f (which is the most computationally costly step of the algorithm), is nearly identical to the previous h computed in the previous evaluation.

In fact, if the new evaluation is the first for a particular move, then h only differs by the move the opposing color made, and the move under consideration. (Keep in mind, because I?m using the thresholding approach, the move corresponding to the last evaluation I computed, and thus, the last h I computed, was actually executed in the game, so I have an accurate starting point in my working memory.)

Thus, in this case, each of the 2048 values of h need to be updated with four operations: One corresponding to the move made by the opposition, one to cancel out where the opposition?s piece was prior to the move, one corresponding to the move under consideration, and one to cancel out where this piece was prior to consideration.

Thus, to update h, only 4 x 2048 = 8192 math operations (additions) are necessary.

If I prepare a certain opening as White, and Magnus responds with the theoretically determined moves, I can come into the game having pre-memorized the first h vector I?ll need, thus only ever having to perform updates.

Of course, if the game veers off script, I?ll need to execute a full evaluation for the first move, but never after that.

Thus, in total, since 4095 operations are still required to convert h to the output y, 8192 + 4095 = 12,287 math operations are needed for an update evaluation.

The memory capacity required also scales down with this update approach, so that only 8192 x 2 + 4096 = 20,480 memory operations are needed per evaluation.

If the evaluation is the second, third, etc. for a particular move, then h only differs by the move previously under consideration and the move currently under consideration. Thus, again, each of the 2048 values of h need to be updated with four operations.

So, this kind of update also requires 12,287 math operations and 20,480 memory operations.

Again, assuming that I can perform one mathematical operation in 3 seconds and one memory operation in 1 second, using this updating approach, I would be able to evaluate one chess position in 57, 341 seconds or 16 hours.

This means that I could complete one full game of chess in 16 hours x 60 evaluations = 40 days.

Clearly, more optimizations are still required, but things are looking better.

In fact, we are starting to get into the range where I could do a David Blaine-style stunt, where I spend 40 days in a jail cell computing chess moves for a one-game extended exhibition.

I think I?d prefer to continue optimizing my algorithm instead, but I?d likely have a price if a very generous sponsor came along. After all, it would be a pretty fascinating human experiment.

Still, tomorrow, I?ll continue to look for ways to improve my computation time.

Hopefully, in the next two days, I can finish all the theoretical planning, have a clear plan in mind, and begin the computer work necessary to generate the actual algorithm.

Yesterday, through some further optimizations, I was able to decrease the run time of my chess evaluation algorithm to 16 hours per evaluation, thus requiring about 40 days for an entire game.

While I?m excited about where this is headed, there?s a problem: Even if this algorithm can be executed in a reasonable time, learning it would be nearly impossible, requiring that I pre-memorize about 1.6 million algorithm parameters (i.e. random numbers) before I even complete my first evaluation.

That?s just too many parameters to try to memorize.

The good news is that it?s probably not necessary to have so many parameters. In fact, the self-driving car algorithm that I built during May, which was based on NVIDIA?s Autopilot model, only required 250,000 parameters.

With this in mind, I suspect that a good chess algorithm only requires about 20,000?25,000 parameters ? an order of magnitude less than the self-driving car, given that a self-driving car needs to make sense of much less structured and much less contained data.

Assuming this is sufficient, I?m completely prepared to pre-memorize 20,000 parameters.

To put this in perspective, in October 2015, Suresh Kumar Sharma memorized and recited 70,030 digits of the number pi.

Thus, memorizing 20,000 random numbers is fully in the possible human range. (I will be truncating the parameters, which span from values of 0 to 1, at two digits, which should maintain the integrity of the function, while also capping the number of digits I need to memorize to 40,000).

Reducing the required number of parameters

In my algorithm from yesterday, most of the parameters came from the multiplication of the 773 digits of bitboard representation with the 2048 rows of the hidden vector h.

Thus, in order to reduce the number of necessary parameters, I can either condense bitboard representation, or choose a smaller width for the hidden layer.

At first, my instinct was to condense bitboard representation down to 37 digits, where the positions in the vector corresponded to particular chess pieces and the numbers at each of these spots corresponded to the particular squares on the board. For example, the first spot in the vector could correspond to the White king, and the value in this spot could span from 1 to 64.

I think an idea like this is worth experimenting with (in the future), but my instinct is that this particular representation is creating too many dependencies/correlations between variables, resulting in a much less accurate evaluation function.

Thus, my best option is to reduce the width of the hidden layer.

I?ve been using 2048 as the width of the hidden layer, which I realized from the beginning is quite large, but I tried to carry it through for as long as possible as a way to force myself to find other large optimizations.

I hypothesize I can create a chess algorithm that is good enough with two hidden layers of width 16, which would require that I memorize 12,640 parameters.

Of course, I need to practically validate this hypothesis by creating and running the algorithm, but, for now, let?s assume this algorithm will work. Even if it works, it may not be time effective, in which case it?s not worth actually building.

So, let?s validate this first?

The new hypothesized algorithm

Unlike the algorithm from the past two days, my hypothesized algorithm has not one, but two hidden layers, which should provide our model with one extra level of abstraction to work with.

This algorithm takes in the 773 digits of the bitboard representation, converts these 773 digits into 16 digits (tuned by 12,368 parameters), converts these 16 digits into another set of 16 digits (tuned by 256 parameters), and outputs an evaluation (tuned by 16 parameters).

This algorithm would require (36 x 16) + (16 x 16) + (15 x 16)+ 16 + 15 = 1103 math operations, (36 x 16) + (16 x 16) + 16 = 848 memory read operations, and 16 + 16 = 32 memory write operations.

Thus, still assuming a 3-second execution time per math operation and a 1-second execution time per memory operation, one evaluation would require (3 x 1,103) + 880 = 4,189 seconds = 1.2 hours to execute.

Of course, as explained yesterday, most evaluations would only be updates on previous evaluations. Using this new algorithm, an update evaluation would require (4 x 16) + (16 x 16) + (15 x 16) + (16 + 15) = 591 math operations, 16 + (4 x 16) + 16 + (16 x 16) + 16 = 368 memory read operations, and 16 + 16 = 32 memory write operations.

Therefore, an update evaluation would require (3 x 591) + 400= 2,173 seconds = 36 minutes to execute.

So, a full game can be played in 36 minutes x 60 evaluation = 36 hours = 1.5 days.

This is still a little long for complete use during a standard chess match, but I could imagine a chess grandmaster using one or two evaluations of this type during a game to calculate a particularly challenging position.

This new algorithm has an execution time of 1.5 days per game, which is almost acceptable, and requires memorizing 12,640 parameters, which is very much in the human range.

In other words, with a few more optimizations, this algorithm is actually playable, assuming that the structure has enough built-in connections to properly evaluation chess positions.

If it does, I might have a chance. If not, I?m likely in trouble.

Time to start testing this assumption?

For the past four days, I?ve been working on a new way to master chess: Constructing and learning a chess algorithm that can be mentally executed (like a computer) to numerically evaluate chess positions.

I still have a lot more work to do on this and a lot more to share.

But, today, I took a break from this work to play some normal games of chess on Chess.com. After all, the better I can evaluate positions without the algorithm, the more effective I will be at using it.

Despite my break, I?m fully committed to my algorithmic approach to chess mastery, as it is the clearest path to rapid chess improvement.

Nevertheless, in the past few days, some of my friends have questioned whether or not I?m actually ?learning chess?. And in the traditional sense, I?m not.

But, that?s only in the traditional sense.

The goal, at the end of the day, is to play a competitive game of chess. The path there shouldn?t and doesn?t matter.

Just because everyone else takes one particular path doesn?t mean that this path is the only path or the best path. Sometimes, it?s worth questioning why the standard path is standard and if it?s the only way to a particular destination.

Of course, it?s still unclear whether or not my algorithmic approach will work, but it?s definitely the path most worth exploring.

Tomorrow, I?ll continue working on and writing about this new approach to learning chess. I?m excited to see how far I can take it?

Today, based on analysis from the past few days, I started building my chess algorithm. The hope is that I can build an algorithm that is both effective (i.e. plays at a grandmaster level), but also learnable, so that I can execute it in my brain.

As I started working, I realized very quickly that I first need to work out exactly how I plan to perform all of my mental calculations. This mental process will inform how I structure the data in my deep learning model.

Therefore, I?ve used this post as a way to think through and document exactly this process. In particular, I?m going to walk through how I plan to mentally convert any given chessboard into a numerical evaluation of the position.

The mental mechanics of my algorithm

First, I look down at the board:

Starting in the a column, I find the first piece. In this case, it?s on a1, and is a Rook. This Rook has a corresponding algorithmic parameter (i.e. a number between -1 and 1, rounded to two places after the decimal point) that I add to the running total of the first sub-calculation. Since this is the first piece on the board, the Rook?s value is added to zero.

The algorithmic parameter for the Rook can be found in my memory, using the following mental structure:

In my memory, I have eight mind palaces that correspond to each of the lettered columns from a to h. A mind palace, as explained during November?s card memorization challenge, is a fixed, visualizable location to which I can attach memories or information. For example, one such location could be my childhood house.

In each mind palace, there are nines rooms, one corresponding to each row from 1 to 8, and an extra room to store the data associated with castling rights. For example, one such room could be my bedroom in my childhood house.

In the first eight rooms, there are six landmarks. For example, one such landmark could be the desk in my bedroom in my childhood house. In the ninth room, there are only four landmarks.

Attached to each landmark are two 2-digit numbers that represent the relevant algorithmic parameters.

The first three landmarks correspond to the White pieces and the second three landmarks correspond to the Black pieces. The first landmark (of each set of three) is used for the algorithm parameters associated with the King and Queen, the second landmark is used for the Rook and Bishop, and the third landmark is used for the Knight and Pawns.

So, when looking at the board above, I start by mentally traveling to the first mind palace (column a), to the first room (row 1), to the second landmark (for the White Rook and Bishop), and to the first 2-digit number (for the White Rook).

I take this 2-digit number and add it to the running total.

Next, I move up the column until I hit the next piece. In this case, there is a White pawn on a2. So, staying in the a mind palace, I mentally navigate to third landmark in the second room, and select the second 2-digit number, which I then add to the running total.

I next move on to the Black pawn on a6, and so on, until I?ve worked my way through the entire board. Then, I enter the ninth room, which provides the 2-digit algorithmic parameters associated with castling rights.

At this point, I take the summed total and store it in my separate 16-landmark mind palace, which holds the values for the first internal output (i.e. the values for the h vector of the first hidden layer).

This completes the first pass of the chessboard, outputting the first of 16 values for h. Thus, I still need to complete fifteen more passes, which repeat the process, but each using a completely new set of mind palaces.

In other words, I actually need 16 distinct mind universes, in which each universe has eight mind palaces of eight rooms of six landmarks and one room of four landmarks.

After completing the process 16 times, and storing each outputted value in the h mind palace, I can move onto the second hidden layer, converting h into h by passing the values of h through a matrix of 256 algorithmic parameters.

These parameters are stored in a single mind palace of 16 rooms. Each room has eight landmarks and each landmark holds two 2-digit parameters.

Unlike the conversion from the chessboard to h, for the conversion of h to h, I almost certainly need to use all 256 parameters in row (unless I implement some kind of squashing function between h and h, reducing some of the hvalues to zero? I?ll explore this option later).

Thus, I start by taking the first value of h and multiplying it (via mental math cross multiplication) by the first value in the first room of the h mind palace. Then, I take the second value of h, multiply it to the second value in the first room, and add the result to the previous result. I continue in this way until I finish multiplying and adding all the terms in the first room, at which point I store the total as the first value of h.

I proceed with the rest of the room, until all the values of h are computed.

Finally, I need to convert h to a single number that represents the numerical evaluation of the given chess position.

To do this, I access one final room in the h mind palace, which has eight landmarks each holding two 2-digit numbers. I multiply the first number in this mind palace with the first value of h, the second number with the second value of h, and so on, adding the results along the way.

In the end, I?m left with a single sum, which should closely approximate the true evaluation of the chess position.

If this number is greater than the determined threshold value, then I should play the move corresponding to this calculation. If not, then I need to start all over with a different potential move in mind.

Some notes:

1. I still need to work out how I plan to store negative numbers in my visual memory.
2. Currently, I?ve only created one mind universe, so, assuming I can computationally validate my algorithmic approach, I?ll need to create 15 more universes. I?ll also need to create a higher level naming scheme or mnemonic system for the universes that I can use to keep them straight in my brain.
3. There is a potential chance that I will need more layers, fewer layers, or different sized layers in my deep learning model. In any of these cases, I?ll need to repeat or remove the procedures, as described above, accordingly.

With the details of my mental evaluation algorithm worked out, I have everything I need to been the computational part of the process.

Today, I started writing a few lines of code, which will be used to generate my chess algorithm. While doing so, I started daydreaming about how this algorithmic approach could change the game of chess if it actually works.

In particular, I tried to answer the question: ?If this works, what?s the ideal outcome??.

There are two parts to this answer?

1. Execution speed

The first part has to do with the execution speed of this method, which I believe can be reduced to less than 10 minutes per evaluation with the appropriate practice.

As a comparable, Alex Mullen, the #1-rated memory athlete in the world, memorized 520 random digits in five minutes. While, one full chess evaluation requires manipulating 816 digits if all the pieces are on the board and 560 digits if half the pieces are on the board.

While these tasks aren?t exactly the same, in my experience, writing numbers to memory takes just about the same times as reading numbers from memory and subsequently adding them.

To be conservative though, I?ve padded Alex?s five minute time, predicting that an expert practitioner at mental chess calculations could execute one chess evaluation in 10 minutes.

At 60 evaluations per game (which is what I predict for myself), an entire game could be completed in 10 hours, which, at least in my eyes, is completely reasonable. Many of the games in this World Chess Championship last for six, seven, or eight hours.

Of course, if a more experienced player can more intelligently implement the algorithm, I suspect she can cut down the number of evaluations per game to around 30, shortening the game to a fairly standard five hours for a classical game.

2. Widespread adoption

I?m not sure if this computational approach to chess will ever catch on as the exclusive strategy of elite players (although, I guess it?s possible), but I can imagine elite players augmenting their games with the occasionally mental algorithmic calculation.

In fact, I wonder if a strong player (2200?2600), who augments her game with this approach, could become a serious threat to the top players in the world.

I?d like to think that, if this works, it?s causes a bit of a stir in the chess world.

It might seem that this approach tarnishes the sanctity of the game, but chess players have been using machine computation for years as part of their training approach. (Chess players use computers to work out the best theoretical lines in certain positions, and then memorize these lines in a rote or intuitive fashion).

Anyway, if this approach to chess does catch on, I might as well give it a catchy name?

At first, I was thinking about something boring like ?Human Computational Chess?, but I?m just going to commit to the more self-serving approach:

Introducing Max Chess: A style of chess play that uses a combination of intuitive moves and mental algorithmic computation. These mental computations are known as Max Calculations.

It?s probably cooler if someone else names a particular technique after you, but I think the cool ship has already sailed, so I?m just going to go with it.

Now, assuming Max Chess even works, let?s see if it catches on?

Today, to accelerate my progress, I thought it might be a good idea to solicit some outside help from someone with a bit more chess AI experience.

So, I shot out a bunch of emails this morning, and surprisingly, received back many replies very quickly. Unfortunately, though, all the replies took the same form?

In other words, no one was interested in collaborating on this project ? or, at least no one was interested in collaborating on this project starting immediately and at full-intensity.

This is understandable.

If I knew that I was going down this algorithmic path at the beginning of the month, and really wanted a collaborator, I should have planned much further in advance.

But, in a way, I?m glad I was rejected. Because now, I have no excuse but to figure out everything on my own.

Ultimately, the purpose of this project is to use time constraints and ambitious goals as motivation to level up my skills, so that?s exactly what I?ll do. Since there?s going to be a little bit of an extra learning curve (given that I?ve never played around with chess data or chess AI previously), this challenge is definitely going to come down to the wire.

But, this time pressure is what makes the project exciting, so here I go? Time to become a master of chess AI.

Side note: To completely negate everything I?ve said above, if you do think you have the relevant experience and are interested in helping out, leave a comment and we?ll figure something out. Always happy to learn from someone else when an option. (And of course always happy to figure it out on my own when it?s not).

Yesterday, after a failed attempt to recruit some help, I realized that I need to proceed on my own. In particular, I need to figure out how to actually produce my (currently) mythical, only theoretical evaluation algorithm via some sort of computer wizardry.

Well, actually, it?s not wizardry ? it just seems that way because I haven?t formalized a tangible approach yet. So, let?s do that in this post.

There are four steps to creating the ultimate Max Chess algorithm:

Step 1: Creating the dataset

In order to train a deep learning model (i.e. have my computer generate an evaluation algorithm), I need a large dataset from which my computer can learn. Specifically, this dataset needs to contain pairs of bitboard representations of chess positions as inputs and the numerical evaluations that correspond to these positions as outputs.

In other words, the dataset contains both the inputs and the outputs, and I?m asking my computer to best approximate the function that maps these inputs to outputs.

There seems to be plenty of chess games online that I can download, including 2,600 games that Magnus has played on the record.

The challenge for this part of the process will be A. Converting the data into my modified bitboard representation (so the data maps one-to-one with my mental process) and B. Generating evaluations for each of the bitboard representations using the open-source chess engine Stockfish (which has a chess rating of around 3100).

Step 2: Creating the model

The next step is to create the deep learning model. Basically, this is the framework for the algorithm to built around.

The model is meant to describe the form that a function (between inputs and outputs in the dataset) should take. However, before training the model, the specifics of the function are unknown. The model simply lays out the functional form.

Theoretical, this model shouldn?t have to deviate too far from already well-studied deep learning models.

I should be able to implement the model in Tensorflow (Google?s library for machine learning) without too much difficulty.

Step 3: Training the model on the dataset

Once the model is built, I need to feed it the entire dataset and let my computer go to work trying to generate the algorithm. This algorithm will map inputs to outputs within the framework of the model, and will be tuned with the algorithm parameters that I?ll need to memorize.

The actual training process should be fairly hands off. The hard part is usually getting the model and the dataset to play nicely with each other, which is honestly where I spent 70% of time during May?s self-driving car challenge.

Step 4: Testing the model and iterating

Once the algorithm is generated, I should test to see at what level it can play chess.

If the algorithm plays at a level far above Magnus, I can simplify and retrain my model, creating a more easily learned and executed evaluation algorithm.

If the algorithm plays at a level below Magnus, I?ll need to create a more sophisticated model, within the limits of what I?ll be able to learn and execute as a human.

During this step, I?ll finally find out if Max Chess has any merit whatsoever.

Now that I have a clear plan laid out, I?ll get started on Step 1 tomorrow.

Yesterday, I laid out my four-step plan for building a human-executable chess algorithm.

Today, I started working on the first step: Creating the dataset.

In particular, I need to take the large corpus of chess games in Portable Game Notation (PGN) and programmatically analyze them and convert them into the correct form, featuring a modified bitboard input and a numerical evaluation output.

Luckily, there?s an amazing library on Github called Python Chess that makes this a lot easier.

As explained on Github, Python Chess is ?a pure Python chess library with move generation and validation, PGN parsing and writing, Polyglot opening book reading, Gaviota tablebase probing, Syzygy tablebase probing and UCI engine communication?.

The parts I?m particular interested in are?

1. PGN parsing, which allows my Python program to read any chess game in the PGN format.
2. UCI (Universal Chess Interface) engine communication, which lets me directly interface with and leverage the power of the Stockfish chess engine for analysis purposes.

The documentation for Python Chess is also extremely good and filled with plenty of examples.

Today, using the Python Chess library, I was able to write a small program that can 1. Parse a PGN chess game, 2. Numerically evaluate each position, and 3. Print out each move, a visualization of the board after each move, and the evaluation (in centipawns) corresponding to each board position.

import chessimport chess.pgnimport chess.uciboard = chess.Board()pgn = open(“data/game1.pgn”)game = chess.pgn.read_game(pgn)engine = chess.uci.popen_engine(“stockfish”)engine.uci()info_handler = chess.uci.InfoHandler()engine.info_handlers.append(info_handler)for move in game.main_line():engine.position(board) engine.go(movetime=2000) evaluation = info_handler.info[“score”][1].cpif not board.turn: evaluation *= -1 print move print evaluation board.push_uci(move.uci()) print board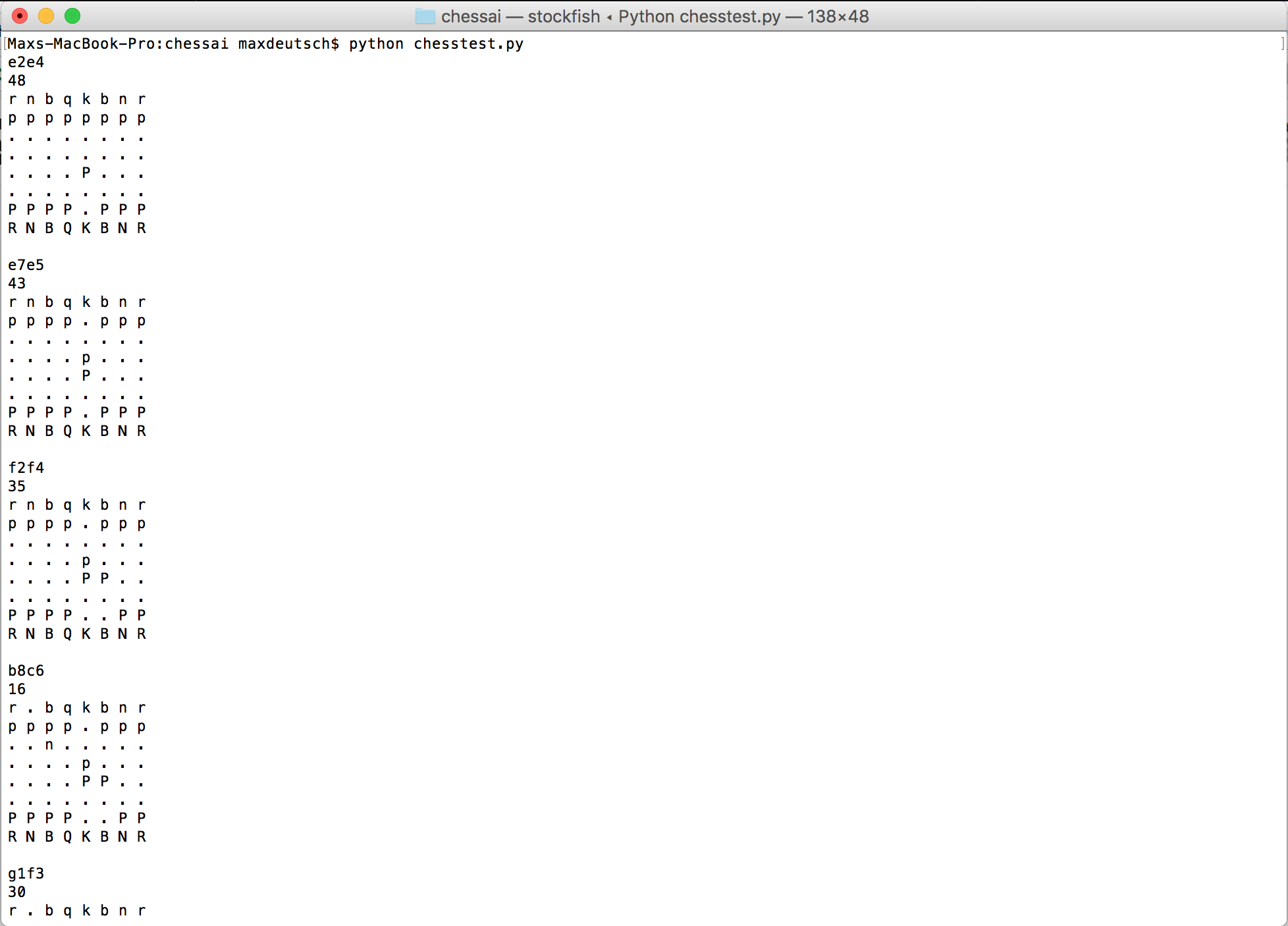

Now, I just need to convert this data into the correct form, so it can be used by my deep learning model (that I?ve yet to build) for the purposes of training / generating the algorithm.

I?m making progress?

Today, I didn?t have time to write any more chess code. So, for today?s post, I figured I?d share the other part of my preparations: The actually games.

Of course, my approach this month has a mostly all or nothing flavor (either I can effectively execute a very strong chess algorithm in my brain, or I can?t), but I?m still playing real chess games on the side to improve my ability to implement this algorithm.

In particular, I?ve been practicing 1. Picking the right moves to evaluate and 2. Playing the right moves without the algorithm when I?m 100% confident.

Recently though, I?ve also been practicing my attacking abilities. In other words, I?ve been trying to aggressively checkmate my opponent?s King during the middle game (compared to my typical approach of exchanging pieces and trying to win in the end game).

Here are three games from today or yesterday that demonstrate my newly aggressive approach. To watch the sped-up playback of the games, click on the picture of the chessboard of the game you want to watch and then click the play button.

Game 1 ? I play White and get Black?s Queen on move 15.

Game 2 ? I play Black and checkmate White in 12 moves

Game 3 ? I play White and checkmate Black in 26 moves

These games aren?t perfect. I still make a few major mistakes per game, and so do my opponents.

In fact, this is one of the biggest challenges with Chess.com: I?m only matched with real people of a similar skill level, which isn?t optimally conducive to improving.

But, I?m still able to test out my new ideas in this environment, while relying on the algorithmic part of my approach for the larger-scale improvements.

Tomorrow, I should hopefully have some time to make more algorithmic progress?

I?m just about to get on a plane from San Francisco to New York, on which I?ll have plenty of time to make progress on my chess algorithm.

Normally, I?d want to actually do the thing and then report back in my post for the day, but, since my flight gets in late, I?ll instead share my plan for what I?m going to do beforehand?

Two days ago, I made a little chess program that can read an inputted chess game and output the numerical evaluation for each move.

Today, during the flight, I?m going to modify this program, so that, instead of outputting a numerical value, it either outputs ?good move? or ?bad move?.

In other words, I need to determine the threshold between good and bad, and then implement this thresholding into my program.

I will attempt to replicate the way that Chess.com implements their threshold between ?good? moves and ?inaccuracies?.

I?ve noticed that, in general, a move is considered to be an inaccuracy if it negatively impacts the evaluation of the game by more than 0.3 centipawns, but I?ve also noticed that this heuristic changes considerably depending on the absolute size of the evaluation (i.e. Inaccuracies are measured differently if the evaluation is +0.75 versus +15, for example).

So, I will need to go through my past Chess.com games, and try to reverse engineer how they make these calculations.

Once I do so, I can implement this thresholding into my program.

For now, as I wait for the plane, I?ve implemented the naive version of this thresholding, where inaccuracies are described by a fixed difference of 0.3.

import chessimport chess.pgnimport chess.uciboard = chess.Board()pgn = open(“data/rickymerritt1_vs_maxdeutsch_2017-10-14_analysis.pgn”)test_game = chess.pgn.read_game(pgn)engine = chess.uci.popen_engine(“stockfish”)engine.uci()info_handler = chess.uci.InfoHandler()engine.info_handlers.append(info_handler)prev_eval = 0diff = 0for move in test_game.main_line():print moveengine.position(board) engine.go(movetime=2000) evaluation = info_handler.info[“score”][1].cpif board.turn: if prev_eval – evaluation > 0.3: print “bad move” else: print “good move” if not board.turn: evaluation *= -1 if evaluation – prev_eval > 0.3: print “bad move” else: print “good move” prev_eval = evaluation board.push_uci(move.uci()) print board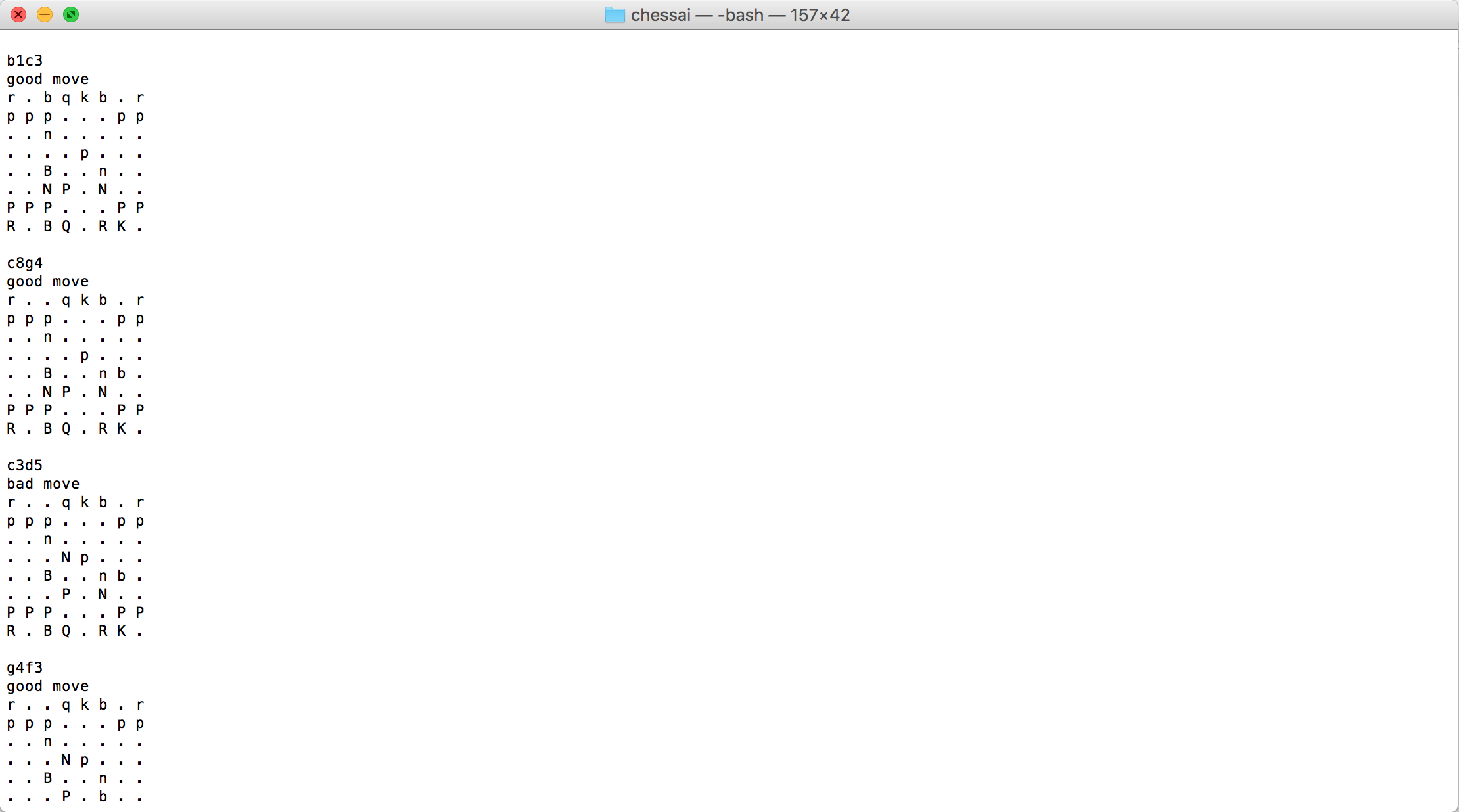

Yesterday, on the plane, I had a really interesting idea: Could a room full of completely amateur chess players defeat the world?s best chess player after less than one hour of collective training?

I think the answer is yes, and, in fact, they could use a distributed version of my human algorithmic approach (i.e. Max Chess) to do so.

In other words, rather than just me learning and computing ever single chess evaluation on my own, instead, each amateur chess player could be in charge of a single mathematical operation, which they could each learn in a few minutes.

By computing mostly in parallel, the entire room of amateur players could evaluate an entire chess board in theoretically a few minutes, letting them not only play at a high level, but also make moves in a reasonable amount of time.

There have been past attempts of Wisdom of the Crowds-style chess games, where thousands of chess players are pitted against a single grandmaster. In these games, each member of the crowd recommends a move and the most popular move is played, while the grandmaster plays as normal.

In the most popular of these games, Garry Kasparov, the grandmaster, defeated a crowd of over 50,000. In other words, the crowd wasn?t so wise.

However, using the distributed algorithmic approach, the crowd would collectively play at the level of an incredible power chess computer. In fact, unlike in my case, the evaluation algorithm can remain reasonably sophisticated, since the computations aren?t restricted by the limits of a single human brain.

Using this approach, we (the amateur chess players of the world) could potentially stage the first crowd vs. grandmaster game where the crowd convincingly defeats a grandmaster, and in style.

To be clear, this doesn?t mean that I?m giving up on my one-man-band approach. I?m still trying to do this completely on my own.

However, I do think this method would scale wonderfully to a larger crowd of people, and if done, the chess game could be played at a speed that may actually be interesting to outside spectators (where as, in my game, I?ll be staring into space for dozens of minutes at a time, mentally calculating).

Maybe, after I complete this month?s challenge, I?ll try to organize a crowd-style algorithmically-inspired chess match.

Today, I went into Manhattan, and, while I was there, I stopped by Bryant Park to play a few games against the chess hustlers.

I wanted to test out my chess skills in the wild, especially since I need more practice playing over an actual chess board.

Apparently, according to chess forums, etc., many players who practice exclusively online (on a digital board) struggle to play as effectively in the real-world (on a physical board). This mostly has to do with how the boards are visualized:

A digital board looks like this?

While a physical board looks like this?

I?m definitely getting used to the digital board, so today?s games in the park were a nice change.

I played three games against three different opponents, with 5 minutes on the clock for each. In all three cases, I was beaten handily. These guys were good.

After the games, now with extra motivation to improve my chess skills, I found a cafe and spent a few minutes working more on my chess algorithm.

In particular, I quickly wrote up the functions needed to convert the PGN chessboard representations into the desired bitboard representation.

def convertLetterToNumber(letter): if letter == ‘K’: return ‘100000000000’ if letter == ‘Q’: return ‘010000000000’ if letter == ‘R’: return ‘001000000000’ if letter == ‘B’: return ‘000100000000’ if letter == ‘N’: return ‘000010000000’ if letter == ‘P’: return ‘000001000000’ if letter == ‘k’: return ‘000000100000’ if letter == ‘q’: return ‘000000010000’ if letter == ‘r’: return ‘000000001000’ if letter == ‘b’: return ‘000000000100’ if letter == ‘n’: return ‘000000000010’ if letter == ‘p’: return ‘000000000001’ if letter == ‘1’: return ‘000000000000’ if letter == ‘2’: return ‘000000000000000000000000’ if letter == ‘3’: return ‘000000000000000000000000000000000000’ if letter == ‘4’: return ‘000000000000000000000000000000000000000000000000’ if letter == ‘5’: return ‘000000000000000000000000000000000000000000000000000000000000’ if letter == ‘6’: return ‘000000000000000000000000000000000000000000000000000000000000000000000000’ if letter == ‘7’: return ‘000000000000000000000000000000000000000000000000000000000000000000000000000000000000’ if letter == ‘8’: return ‘000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000’ if letter == ‘/’: return ”def convertToBB(board): bitBoard = ” board = str(board.fen()).split(‘ ‘)[0] for letter in board: bitBoard = bitBoard + convertLetterToNumber(letter) return bitBoardprint convertToBB(board)

While I?m making some progress on the algorithm, since I?ve been in New York, I haven?t made quite as much progress as I hoped, only spending a few minutes here and there on it.

Let?s see if I can set aside a reasonable chunk of time tomorrow to make some substantial progress?

Today, I turned a corner in my chess development: I?m finally starting to appreciate the beauty in the game, which is fueling my desire to improve my chess game in the traditional way, in addition to the algorithmic way.

Before starting this month?s challenge, I was a bit concerned about studying chess. In particular, I imagined that learning chess was just memorizing predetermined sequences of moves, and was worried that, by simply converting chess to memorized patterns, the game would lose some of its interest to me.

In the past, while playing chess with friends, I?ve enjoyed my reliance on real-time cleverness and intuition, not pattern recognition. I feared I would lose this part of my game, as I learned more theory and began to play more like a well-trained computer.

Ironically, this fear came true, but not in the way that I expected. After all, my main training approach this month (my algorithmic approach) effectively removes all of the cleverness and intuition from the gameplay, and instead, treats chess like one big, boring computation.

This computational approach is still thrilling to me though, not because it makes the actual game more fun, but because it represents an entirely new method of playing chess.

Interestingly though, adding to my chess knowledge in the normal way hasn?t reduced my intellectual pleasure in the game as I expected. In fact, it has increased it.

The more I see and understand, the more I can appreciate the beauty of particular chess lines or combinations of moves.

Sure, there are certain parts of my game that are now more mechanical, but this allows me to explore new intellectual curiosities and combinations at higher levels. It seems there is always a higher level to explore (especially since my chess rating is around 1200, while Magnus is at 2822 and computers are at around 3100).

The more normal chess I?ve learned this month, the more I?m drawn to pursuing the traditional approach. There is just something intellectually beautiful about the game and the potential to make ever-continuing progress, and I?d love to explore this world further.

With that said, this isn?t a world that can fully be explored in one month, so I?m happily continuing with primary focus on my algorithmic approach.

To be clear, I?m not pitting the algorithmic approach against the traditional approach. Instead, I?m saying: ?Early in this month, I fell in love with the mathematical beauty of and the potential to break new ground with the algorithmic approach. Just today, I?ve finally found a similar beauty in the way that chess is traditionally played and learned, and also want to explore this further?.

In other words, this month, I?m developing two new fascinations that I can enjoy, appreciate, and explore for the rest of my life.

This is the great thing about the M2M project: It has continually exposed me to new, personally-satisfying pursuits that I can continue to enjoy forever, even once the particular month ends.

Today, my brain suddenly identified traditional chess as one of these lifelong pursuits.

If I had this appreciation for traditional chess at the beginning of the month, I wonder if I would have so easily and quickly resorted to the algorithmic approach, or if I would have been held back by my romanticism for the ?normal way?.

Luckily, this wasn?t the case, and now I get to explore both in parallel.

Today, I finished writing the small Python script that converts chess games downloaded from the internet into properly formatted data needed to train my machine learning model.

Thus, today, it was time to start building out the machine learning model itself.

Rather than starting from scratch, I instead looked for an already coded-up model on Github. In particular, I needed to find a model that analogizes reasonably well to chess.

I didn?t have to look very hard: The machine learning version of ?Hello World? is called MNIST, and it works perfectly for my purposes.

MNIST is a dataset that consists of 28 x 28px images of handwritten digits like these:

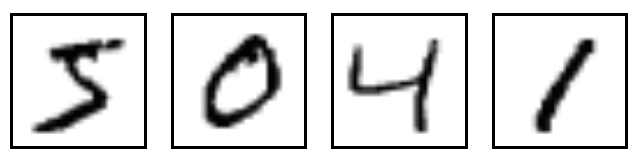
The dataset also includes ten labels, indicating which digit is represented in each image (i.e. the labels for the above images would be 5, 0, 4, 1).

The objective is to craft a model that, given a collection of 28 x 28=784 values, can accurately predict the correct numerical digit.

In a very similar way, the objective of my chess model, given a collection of 8 x 8 = 64 values (where each value is represented using 12-digit one-hot encoding), is to accurately predict whether the chess move is a good move or a bad move.

So, all I need to do is download some example code from Github, modify it for my purposes, and let it run. Of course, there are still complexities with this approach (i.e. getting the data in the right format, optimizing the model for my purposes, etc.), but I should be able to use already-existing code as a solid foundation.

Here?s the code I found:

from __future__ import absolute_importfrom __future__ import divisionfrom __future__ import print_functionimport argparseimport sysfrom tensorflow.examples.tutorials.mnist import input_dataimport tensorflow as tfFLAGS = Nonedef main(_): # Import data mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)# Create the model x = tf.placeholder(tf.float32, [None, 784]) W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) y = tf.matmul(x, W) + b# Define loss and optimizer y_ = tf.placeholder(tf.float32, [None, 10])# The raw formulation of cross-entropy, cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)) train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)sess = tf.InteractiveSession() tf.global_variables_initializer().run() # Train for _ in range(1000): batch_xs, batch_ys = mnist.train.next_batch(100) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})# Test trained model correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))if __name__ == ‘__main__’: parser = argparse.ArgumentParser() parser.add_argument(‘–data_dir’, type=str, default=’/tmp/tensorflow/mnist/input_data’, help=’Directory for storing input data’) FLAGS, unparsed = parser.parse_known_args() tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

Tomorrow, I?ll take a crack at modifying this code, and see if I can get anything working.

Parkinson?s Law states that ?work expands so as to fill the time available for its completion?, and I?m definitely experiencing this phenomenon during this final M2M challenge.

In particular, at the beginning of the month, I decided to extend this challenge into early November, rather than keeping it contained within a single month. I did this for a good reason, which I?ll explain soon, but this extra time isn?t exactly helping me.

Instead, I?ve simply adjusted my pace as to fit the work to the extended timeline.

As a result, in the past week, especially since I?m currently visiting family, I?ve found it challenging to make focused progress for more than a few minutes each day.

So, in order to combat this slowing pace and start building momentum, I?ve decided to set an interim deadline: By Sunday, October 29, I must finish creating my chess algorithm and shift my focus fully to learning and practicing the algorithm.

This gives me one week to 1. Build the machine learning model, 2. Finish creating the full dataset, 3. Testing the trained model, 4. Making further optimizations, 5. Testing the strength of the chess algorithm, and, in general, 6. Validating or invalidating the approach.

Hopefully, with this interim deadline in place, I feel a greater sense of urgency and can overcome the friction of Parkinson?s Law.

Two days ago, I found some code on Github that I should be able to modify to create my chess algorithm. Today, I will dissect the code line by line to ensure I fully understand it, preparing me to create the best plan for moving forward.

Again, the code that I found is designed to take in an input image (of size 28 x 28 pixels, as shown below) and output a prediction of the numerical digit handwritten in the image.

Here?s the code in its entirety:

from __future__ import absolute_importfrom __future__ import divisionfrom __future__ import print_functionimport argparseimport sysfrom tensorflow.examples.tutorials.mnist import input_dataimport tensorflow as tfFLAGS = Nonedef main(_): # Import data mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)# Create the model x = tf.placeholder(tf.float32, [None, 784]) W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) y = tf.matmul(x, W) + b# Define loss and optimizer y_ = tf.placeholder(tf.float32, [None, 10])# The raw formulation of cross-entropy, cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)) train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)sess = tf.InteractiveSession() tf.global_variables_initializer().run() # Train for _ in range(1000): batch_xs, batch_ys = mnist.train.next_batch(100) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})# Test trained model correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))if __name__ == ‘__main__’: parser = argparse.ArgumentParser() parser.add_argument(‘–data_dir’, type=str, default=’/tmp/tensorflow/mnist/input_data’, help=’Directory for storing input data’) FLAGS, unparsed = parser.parse_known_args() tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

Part 1: Importing the necessary libraries and helper functions

The first seven lines of code are used to important the necessarily libraries and helper functions required to build the machine learning model.

from __future__ import absolute_importfrom __future__ import divisionfrom __future__ import print_functionimport argparseimport sysfrom tensorflow.examples.tutorials.mnist import input_dataimport tensorflow as tf

Most importantly, line 6 (?from tensorflow.examples.tutorials.mnist import input_data?) is used to import the dataset, and line 7 (?import tensorflow as tf?) is used to import the TensorFlow machine learning framework.

I can keep these seven lines as is, except for line 6, which will depend on the format of my chess data.

Part 2: Reading the dataset

The next four lines are used to read the dataset. In other words, these lines convert the data into a format that can be used within the rest of the program.

FLAGS = Nonedef main(_): # Import data mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)

This is the part of the code that is most intimidating to me, but I have a few ideas.

Firstly, based on the documentation that accompanies the Github code, it seems that the data is prepared in a fairly straightforward way, contained within two matrices:

1. The first matrix has dimensions of 784 by 55,000, where 784 represents the number of pixel in the image and 55,000 represents the number of images in the dataset.
2. The second matrix has dimensions of 10 by 55,000, where 10 represents the labels (i.e. digit names) for each image, and again 55,000 represents the number of images.

I should be able to prepare two similar matrices for my chess data, even if I don?t do it in a particularly fancy way. In fact, I might construct these matrices in a Python format and then just copy and paste them into the same file as the rest of the code, so I don?t have to worry about actually reading the data into the program, etc.

This sounds a little hacky, but should do the trick.

In fact, to confirm the shape of the data, I modified the program, asking it simply to print out the the array representing the first image:

from __future__ import absolute_importfrom __future__ import divisionfrom __future__ import print_functionimport argparseimport sysfrom tensorflow.examples.tutorials.mnist import input_dataimport tensorflow as tfFLAGS = Nonedef main(_): # Import data mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True) print(mnist.test.images[0]) if __name__ == ‘__main__’: parser = argparse.ArgumentParser() parser.add_argument(‘–data_dir’, type=str, default=’/tmp/tensorflow/mnist/input_data’, help=’Directory for storing input data’) FLAGS, unparsed = parser.parse_known_args() tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

And here?s what it printed:

It looks like each of these image arrays are then nested inside of another, larger array. In particular, here?s the output if I ask the program to print all of the image arrays:

In other words, I need to prepare my data in a set of 773-digit arrays (one array for each chessboard configuration) nested inside of a larger array.

For the labels, in my case ?good move? and ?bad move?, I need to nest 2-digit arrays (one array for each chessboard label), inside of a larger array.

In this case, [1, 0] = good move and [0,1] = bad move. This kind of structure matches the ?one_hot=True? structure of the original program.

The original program likely separates all of the labels out in this way, rather than using binary notation, to indicate that the labels aren?t correlated to each other.

In the chess case, the goodness or badness of a move is technically correlated, but I?ll stick with the one hot structure for now.

Part 3: Create the model

The next five lines of code are used to define the shape of the model.

# Create the model x = tf.placeholder(tf.float32, [None, 784]) W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) y = tf.matmul(x, W) + b

In this case, there are no hidden layers. The function is simply mapping inputs directly to outputs, with no intermediate steps.

In the above example, 784 represents the size of an image and 10 represents the number of possible labels.

In the same way, for my chess program, 773 represents the size of a chessboard representation, and 2 represents the number of possible labels.

So, I can update the code, for my purposes, in the following way:

# Create the model x = tf.placeholder(tf.float32, [None, 773]) W = tf.Variable(tf.zeros([773, 2])) b = tf.Variable(tf.zeros([2])) y = tf.matmul(x, W) + b

Of course, I?m skeptical that a model this simplistic will play chess at a sufficiently high level. So, I can modify the code to support my more sophisticated model, which has two hidden layers, first mapping the 773 bits of the chessboard to 16 interim values, which are then mapped to another 16 interim values, which are then finally mapped to the output array.

# Create the model x = tf.placeholder(tf.float32, [None, 773]) W1 = tf.Variable(tf.zeros([773, 16])) b1 = tf.Variable(tf.zeros([16])) h2 = tf.matmul(x, W1) + b1 W2 = tf.Variable(tf.zeros([16, 16])) b2 = tf.Variable(tf.zeros([16])) h2 = tf.matmul(h2, W2) + b2 W3 = tf.Variable(tf.zeros([16, 2])) b3 = tf.Variable(tf.zeros([2])) y = tf.matmul(h2, W3) + b3

Part 4: Training the model

Now that we have the framework for our model setup, we need to actually train it.

In other words, we need to tell the program how to recognize if a model is good or bad. A good model does a good job approximating the function that correctly maps chess positions to evaluations, while a bad model does not.

# Define loss and optimizer y_ = tf.placeholder(tf.float32, [None, 10])# The raw formulation of cross-entropy, cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)) train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

For our purposes, we define a function called the Cross Entropy, which basically outputs how bad the model?s predictions are compared to the true values, which we use to test the quality of our model during training. For as long as the model is still bad, we use a mathematical technique called Gradient Descent to minimize the Cross Entropy until it?s below an acceptably small amount.

For implementation purposes, it?s not important to understand the math underlying either Cross Entropy or Gradient Descent. For my purposes this is both good and bad: It?s bad because I?m much stronger on the theoretical, mathematical side of machine learning versus the implementation side. It?s good because I?m forced to improve my abilities on the implementation side.

Part 5: Test the trained model

Once the model is trained, we want to test how well the model actually performs by comparing what the model predicts against the true labels in the dataset.

# Test trained model correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

When the model outputs a prediction, it outputs a 10-digit array, where each digit of the array is a number between 0 and 1. Then, this array is fed into the function tf.argmax(y, 1), which outputs the label corresponding to the position in the array with the value closest to 1.

Part 6. Run the program

Finally, there?s some code that?s needed to make the program actually run:

if __name__ == ‘__main__’: parser = argparse.ArgumentParser() parser.add_argument(‘–data_dir’, type=str, default=’/tmp/tensorflow/mnist/input_data’, help=’Directory for storing input data’) FLAGS, unparsed = parser.parse_known_args() tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

Now that I?ve digested the entire program and convinced myself that I understand what?s going on, I?ll start playing around with it tomorrow and see if I can output any initial results.

Yesterday, I deconstructed, line by line, the code that I?m using to generate my chess algorithm. Today, I explored this code a little bit further.

In particular, I wanted to answer two questions today:

Question 1

Once I fully train the machine learning model, how do I output the resulting algorithmic parameters in a readable format (so that I can then proceed to memorize them)?

In my code, the variable W represents the matrix that holds all of the algorithm parameters, so I figured that I could just run the command print(W).

However, unlike normal Python code, Tensorflow does not allow for this kind of syntax.

After a little playing around, I discovered I need to run a Tensorflow Interaction Session in order to extract the values of W.

This isn?t anything theoretically fancy. It?s simply the syntax that Tensorflow requires?

sess = tf.InteractiveSession()tf.global_variables_initializer().run()for i in range(0,784): for j in range(0,10): param = sess.run(W)[i][j] print(round(param,2))

And here?s the output ? a list of all 7840 parameters contained in W:

You?ll notice that I?m using the round function to round all of the parameters to two digits after the decimal point, as this is the limit for what my human brain can handle.

I still need to figure out how to update these values within W, and then validate that the model still works reasonably well with this level of detail. (If it doesn?t, then my algorithmic approach is in big trouble).

Question 2

Does my more sophisticated model actually produce better results? And if it does, are the results better by enough to justify the extra complexity?

If I just run the sample code as it (where the code is trying to identify handwritten numerical digits in input images), the model predicts the correct digit 92% of the time, which isn?t too bad.

If I make the model in the sample code more sophisticated, by adding two hidden layers, and then retesting its predictions, it only correctly identifies digits 11% of the time (i.e. essentially no better than a random guess).

I?m not sure if I simply don?t have enough data to train this more sophisticated model, or if there?s a gap in my understand in regards to building more sophisticated models.

If it?s a data problem, I can resolve that. If it?s a gap in my understand, I can resolve that too, but it may uncover some potential obstacles for my algorithm chess approach.

Hopefully, I can find a way forward. Hopefully, there?s even a way forward.

Today, I had a good idea. In fact, after some brainstorming with a friend, I figured out a surefire way to complete this month?s challenge.

It?s important to mention that this idea was heavily inspired by Nathan Fielder of Comedy Central?s Nathan for You, which is currently the only TV show I?m watching. While the humor of the show probably isn?t for everyone, I find the show brilliant and immensely satisfying.

Anyway, here?s the idea:

As I defined this month?s challenge, I need to defeat world champion Magnus Carlsen at a game of chess.

It turns out that, based on this definition of success, there actually is one minor loophole: I didn?t specify that Magnus Carlsen needs to be the World Chess Champion. Rather, I just specified that he need to be a world champion.

In other words, I don?t need to defeat the Magnus Carlsen at a game of chess. I just need to defeat a Magnus Carlsen at a game of chess, as long as this Magnus Carlsen is the world champion at anything.

Firstly, after a quick search on Facebook, I found dozens of other Magnus Carlsens who would be perfect candidates for my chess match. I guess Magnus Carlsen is a reasonably popular nordic name.

Even if I couldn?t convince any of these other Magnus Carlsens to participate, I can alway find someone who?d be willing to change their name if properly compensated. (In Nathan?s show, in one of the episodes, he pays a guy from Craigslist $1,001 to change his name).

Once I have a willing Magnus Carlsen, I?ll need to ensure that he is the world champion at something.

This is an incredibly flexible constraint?

I could even ask Magnus Carlsen #2 to invent a new board game that only he knows the rules for, guaranteeing that he is the world champion. Of course, I would stage a world championship event just to be sure.

Then, assuming Magnus Carlsen #2 isn?t a very good chess player, we?d play a game of chess and I?d easily defeat him, thereby allowing me to officially defeat world champion Magnus Carlsen at a game of chess.

Clearly, the point of my M2M project isn?t to bend semantics, but I did find this idea amusing. And, not only that, but it is technically legitimately.

Anyway, the purpose of sharing this, other than perhaps amusing one other person, is to say that there are always many creative ways to reach you goals. Sometimes, you just need to think a little differently.

My flight from New York to San Francisco just landed, which means that I?ll be back to my regular routine tomorrow. As part of this ?regular routine?, I plan to greatly accelerate my chess efforts.

For the past eight days, I was in New York, primarily for a family function that lasted through the weekend (Friday through Sunday). During the six weekdays that I was in New York, staying at my parent?s house, I was still working full time. This wasn?t a vacation.

As a result, I needed to make a decision about how I wanted to use my extracurricular time in the evenings.

Typically, I mainly use this time for my M2M project and related activities, but, given that I haven?t seen my parents, sisters, or extend family for months, and don?t see them very often, I wanted to allocate a lot of this time to spend with them.

As a result, truthfully, in the past eight days, I probably spent a total of two hours working directly on my chess preparations, which isn?t very much at all.

But this was largely by design: I decided that I would prioritize time with my family over doing work (in all the forms that takes), and that I would find extra work time in the coming weeks, now that I?m back in San Francisco, to balance things out.

It?s often challenging to prioritize time with friends, family, etc., and similarly challenging to prioritize time to relax, play, and think, since these activities don?t have any timelines, deadlines, or ways to measure productivity or progress. It?s especially challenging to prioritize these activities when there are other available activities that do offer a greater sense of progress, productivity, or urgency.

We, as humans, want to feel important and often use progress or productivity (or even unnecessary busyness) as a way to prove to ourselves that we are important.

But, we can also be important just by enjoying the love we share with others (by spending time with friends and family) and by enjoying the love we have for ourselves (by relaxing, playing, exploring, etc.).

In fact, when I reflect on my life, my strongest memories are either of the times I spent with people I love or of the times I explored new places or things (traveling, learning new things, etc.).

Of course, when I was in New York, there was the option to lock myself in my bedroom and pound out chess code for hours. In fact, if I took this approach, I?d likely be in a better place with my preparations right at this moment.

However, I very happily sacrificed some of this preparation time for a lot of great time with my family. And, the truth is? I didn?t sacrifice this time at all. I simply decided to reallocate it to this upcoming week.

Often, in our lives, we create a fake sense of urgency around things that, when we zoom out, aren?t so urgent or grand after all. It?s very easy to chase these ?urgent things? our entire lives, preventing us from enjoying much of what life has to offer.

I?m not perfect at resisting this temptation, but this past week was good practice in doing so and reaping the benefits.

With that said, now that I?m back in San Francisco, I?m going to reestablish this massive, largely artificial sense of importance and urgency that surrounds this month?s challenge.

So, here I go?

Today, I finally got back to working on my chess algorithm, which I?m hoping to finish by Sunday night.

I started by throwing out all of the code I previously had, which I just couldn?t make work.

After watching a few Tensorflow tutorials on YouTube, I was able to write a new program that works with CSV datasets. I was even able to get it to run on a tiny, test dataset:

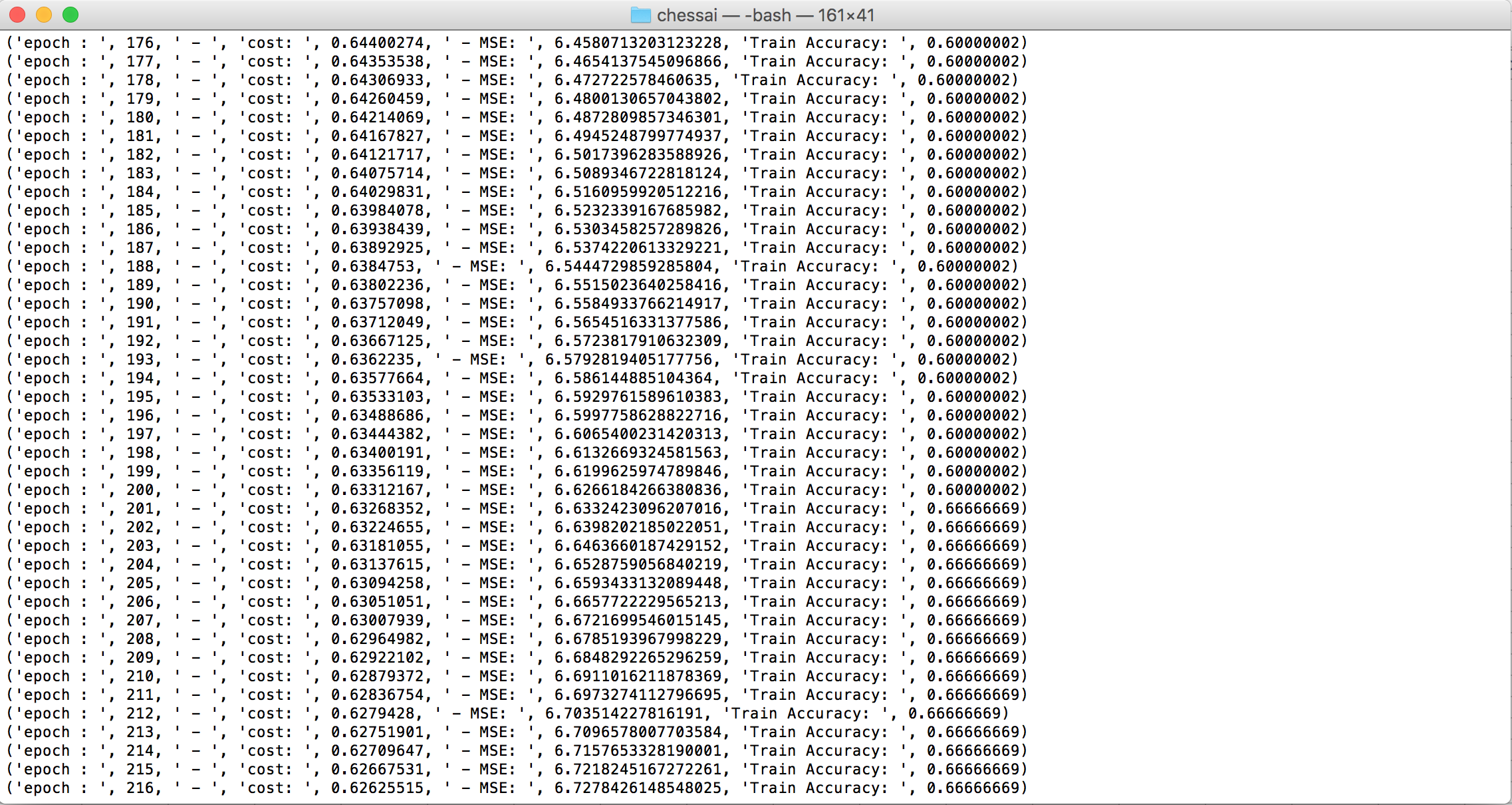
Now that I had figured out how to import a dataset into a Python program, and then subsequently run it through a machine learning model, I needed to expand my data processing program from a few days ago, so that I could convert chess games in PGN format into rows in my CSV file.

Here?s what those changes look like:

import chessimport chess.pgnimport chess.uciboard = chess.Board()pgn = open(“data/caruana_carlsen_2017.pgn”)test_game = chess.pgn.read_game(pgn)engine = chess.uci.popen_engine(“stockfish”)engine.uci()info_handler = chess.uci.InfoHandler()engine.info_handlers.append(info_handler)prev_eval = 0diff = 0output_data_string = ”def convertLetterToNumber(letter): if letter == ‘K’: return ‘1,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘Q’: return ‘0,1,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘R’: return ‘0,0,1,0,0,0,0,0,0,0,0,0,’ if letter == ‘B’: return ‘0,0,0,1,0,0,0,0,0,0,0,0,’ if letter == ‘N’: return ‘0,0,0,0,1,0,0,0,0,0,0,0,’ if letter == ‘P’: return ‘0,0,0,0,0,1,0,0,0,0,0,0,’ if letter == ‘k’: return ‘0,0,0,0,0,0,1,0,0,0,0,0,’ if letter == ‘q’: return ‘0,0,0,0,0,0,0,1,0,0,0,0,’ if letter == ‘r’: return ‘0,0,0,0,0,0,0,0,1,0,0,0,’ if letter == ‘b’: return ‘0,0,0,0,0,0,0,0,0,1,0,0,’ if letter == ‘n’: return ‘0,0,0,0,0,0,0,0,0,0,1,0,’ if letter == ‘p’: return ‘0,0,0,0,0,0,0,0,0,0,0,1,’ if letter == ‘1’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘2’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘3’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘4’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘5’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘6’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘7’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘8’: return ‘0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,’ if letter == ‘/’: return ”def convertToBB(board): bitBoard = ” board = str(board.fen()).split(‘ ‘)[0] for letter in board: bitBoard = bitBoard + convertLetterToNumber(letter) bitBoard = bitBoard[1:-1] return bitBoardfor move in test_game.main_line(): engine.position(board) engine.go(movetime=2000) evaluation = info_handler.info[“score”][1].cp evaluation_label = “”if board.turn: if prev_eval – evaluation > 0.3: evaluation_label = “B” #badmove else: evaluation_label = “G” #goodmove if not board.turn: evaluation *= -1 if evaluation – prev_eval > 0.3: evaluation_label = “B” #badmove else: evaluation_label = “G” #goodmove prev_eval = evaluation board.push_uci(move.uci()) out_board = convertToBB(board) output_data_string = output_data_string + out_board + ‘,’ + evaluation_label + ‘n’ f = open(‘chessdata.csv’,’w’)f.write(output_data_string)f.close()

And, here?s the output? (Each row has 768 columns of 1?s and 0?s corresponding to a bitboard representation of a chess position, and the 769th column is either a G or a B, labeling the chess position as ?good? or ?bad? accordingly. I haven?t yet encoded castling rights. I?ll do that once I can get my current setup to work.)

With this done, I had the two pieces I needed: 1. A way to convert chess positions into CSV files, and 2. A way to read CSV files into a machine learning model.

However, when I tried to put them together, the program wouldn?t run. Instead, I just got errors like this one?

pandas.errors.ParserError: Error tokenizing data. C error: Expected 2 fields in line 8, saw 5

?suggesting that my dataset was ?dirty? in some capacity.

And this one?

ValueError: Cannot feed value of shape (43, 1) for Tensor u?Placeholder_1:0′, which has shape ?(?, 2)?

?suggesting that my data wasn?t conforming to the machine learning model, which is also likely a result of ?dirty? data.

I tried to clean up the data by hand, but continued getting error messages.

Eventually, I discovered that I was generating a CSV file that sometimes contained two commas in a row (see below), which was causing my problems.

I found the bug in my data processing program, and then tried to run my machine learning model on the dataset again.

Finally, it worked (in the sense that it was running), but it was failing to calculate the ?cost function?, which is one of the most important ingredients to the machine learning training process.

I was able to reduce the dataset down, and get it to train normally (with a calculated cost, etc.), but, for some reason, when scaling it up to the full dataset, something is breaking down.

Tomorrow, I?ll try to diagnose the problem.

Nevertheless, I made a ton of progress today, and nearly have everything working together. Once everything?s working, I suspect I will need to spend some time optimizing the model (i.e. finding the optimal balance between maximum chess performance and maximum learnability).

Yesterday, after a focused, 90-minute coding session, I was nearly able to get my program to read a CSV representation of a chess position, and then, use it to train a machine learning model.

Today, I was able to identify and fix the bug in yesterday?s code, letting me successfully run the program and train my model.

I then wrote some code that takes the parameters of the outputted model and writes them to a CSV file like this:

With this done, I?ve officially completed the full chess algorithm pipeline.

Here?s what the pipeline can do:

1. Takes a chess game downloaded from the internet and converts it into a correctly formatted CSV. The CSV file contains the bitboard (i.e. 1?s and 0?s) representation of the chess position, and labels each chess position as either ?good? or ?bad?, using the Stockfish chess engine to compute all the evaluations.
2. Reads the CSV file into a machine learning program, randomizes the order of the data, divides the data into a training dataset and a testing dataset, trains a machine learning model on the training dataset, and tests the model?s performance on the testing dataset.
3. Once the model is tuned so that it can properly determine ?good? and ?bad? chess positions, it outputs the algorithmic parameters to another, properly-organized CSV file. Soon, I?ll use this file to memorize all of the algorithmic parameters, effectively transforming my brain into a chess computer.

Almost all of this code was written in the past two days (over the span of two hours), which is pretty amazing considering I?ve made very incremental progress for the past two weeks.

Clearly, a fully focused and committed approach goes a long way.

Yesterday, I finished building my chess algorithm pipeline, which can take chess games downloaded from the internet, convert them into a machine learning-friendly format, and then use them to train a machine learning model. At the end of the pipeline, the program outputs a list of algorithmic parameters that I can memorize and eventually use to compute chess evaluations in my brain.

This was great progress, but, as of yesterday, there was still a problem: The part of my program that is meant to label each chess position with either ?good? or ?bad? (so that the machine learning model knows how to properly evaluation the position) didn?t actually work at all?

In other words, the program outputted ?good? and ?bad? labels nearly at random, not actually tied to the true evaluation of the chess position.

Clearly, if my data is poorly labeled, even if I can build an incredibly accurate machine learning model, the resulting chess algorithm will still be just as ineffective as the data is bad.

So, today, I worked on addressing this problem.

In particular, I continuously tweaked my program until its outputs matched the ?true? evaluations of the positions.

As my source of truth, I used the website lichess.org, which allows users to import and analyze chess games, explicitly identifying all the bad moves (inaccuracies, mistakes, and blunders) in the given game:

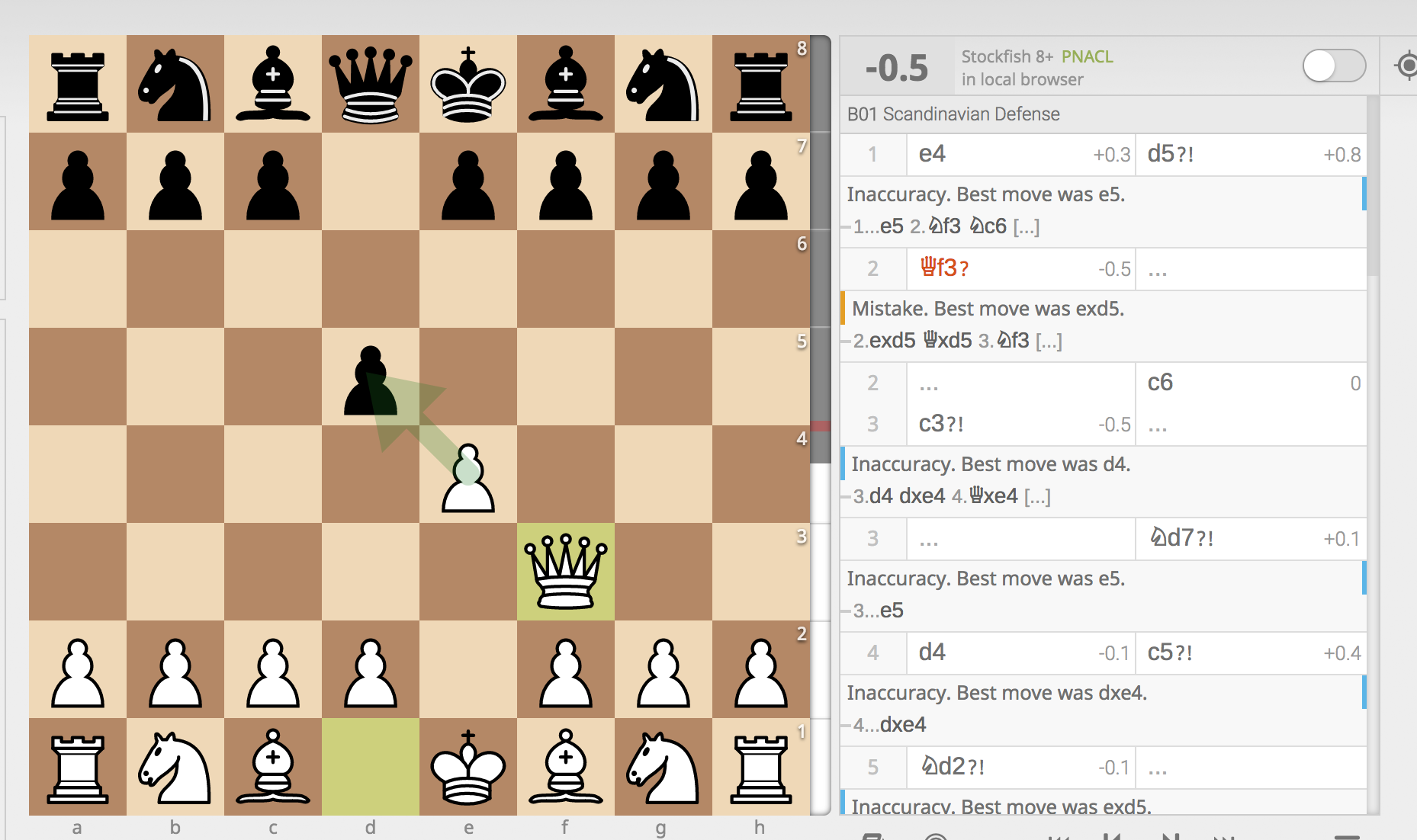
After about 30 minutes of work, I was able to get my program to exactly mirror the evaluations of lichess across every chess game that I tested.

So, I was finally ready to generate my correctly-label dataset.

As of yesterday, the program in my pipeline that converts chess games into CSV files could only handle one game at a time. Thus, today, I augmented the program so that it can cycle through millions of games on its own.

I?m using the chess database from lichess.org (which contains over 200 million chess games) to generate my properly label dataset.

Right now, I?m running all of the September 2017 games (which is about 12 million games) through my program.

Because the program needs to deeply evaluate each position, using the Stockfish chess engine with a depth of 22, the program is taking a long time to run. It looks like it will only be able to crunch through about 150 games every 24 hours, or approximately 6,000 chess positions, if I continue to run it just on my local computer.

Also, I can only use half of these chess positions for my training dataset, given that I?m currently only training my model to play with the White pieces.

I?m not sure how many chess positions I?ll need in order to train a decently functional model, but I?m guessing somewhere between 25,000?50,000 should be enough, which will take about a week to generate at the high end.

With that said, the program is iteratively writing each evaluated chess position to the CSV file in real-time, so I can start playing around with the data that?s already processed as the other games are still processing.

Yesterday, I predicted that I would be able to process 150 chess games every 24 hours. It?s been 24 hours since that prediction, and, in reality, I?m processing more like 350 games every 24 hours.

In fact, so far, I?ve evaluated 10,000 chess positions (as either good or bad) and have written these evaluations to my training_dataset CSV file, ready for consumption by my machine learning model.

Although I still need a lot more data, today, at around 2pm, I started training my model on what data I had, just to see what would happen.

In the beginning, the accuracy of the model, as measured on the training data, was only slightly more than 50% (i.e. a completely random evaluation, good or bad, of the chess positions).

Eight hours later, after 10,000 iterations through the 7,000 chess positions (3,000 chess positions have processed since then), the model?s accuracy on the training data leveled off at around 99%.

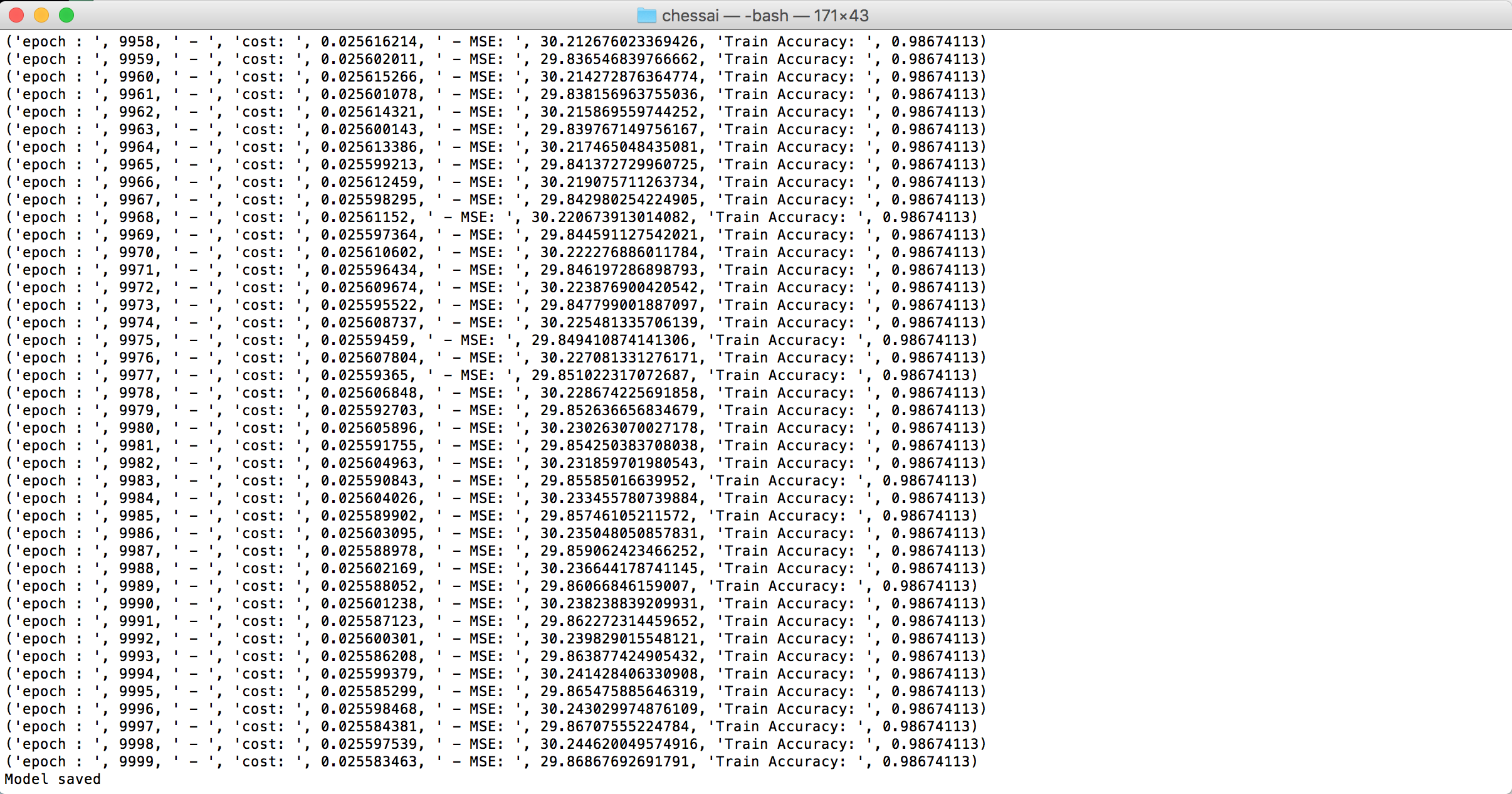
At first, I didn?t realize that this accuracy was based on the training data, so I thought this was unbelievably good. In other words, I thought this accuracy number represented how the model performed on data it had never seen before (while in reality the model was optimizing itself around this exact data).

When I tested the model on genuine test data (i.e. data the model truly had never seen before), it was only able to correctly evaluate the position about 70% of the time, which is not great.

I?m hoping I can improve this performance with a lot more data, but I may also need to add sophistication to the model.

Of course, the more data, the longer the model is going to take to run, which means the slower I?ll be able to iterate on my approach.

I could really use some special hardware right about now to speed things up? I may need to look into cloud compute engines to give me a little extra boost.

I?m still making progress, but a 70% performance is a bit of a letdown after I waited nearly eight hours to see the results.

Yesterday, after eight hours of processing, I was able to test the first version of my chess algorithm.

Sadly, it was only able to correctly evaluate chess positions as good or bad 70% of the time, which isn?t very good for my purposes.

Of course, this algorithm was created only based on 300 chess games, while I have access to over 200 million games. So, hopefully the algorithm will become more accurate as I feed it significantly more data.

Even if I can create an algorithm that is 99% accurate though, it?s still unclear how well this algorithm can be used to play chess at a high level.

In other words, even if I can identify and play ?good? chess moves with 99% accuracy, is this enough to defeat the world?s best chess player?

In order to find out, I built a program today that let?s me test out my algorithm within actual gameplay. Here?s how it works:

1. Since I?m playing with the White pieces, I make the first move. To do so, I suggest a move to the program.
2. The program then runs this move through my algorithm and decides whether the move is good or bad.
3. If it?s good, the program automatically plays the move. If not, it asks me to suggest another move until I find a good move.
4. Then, my opponent responds with the Black pieces. I enter Black?s move into the program.
5. After Black?s move is recorded, I suggest my next move, which is again played if the move is evaluated to be good.
6. And so, until the game is over.

Here?s what the program looks like running in my Terminal:

In this way, I can test out different chess algorithms to see how they perform against chess computers of different strengths.

If I can find an algorithm that, when used in this way, allows me to defeat Magnus Age 26, within the Play Magnus app, then I can proceed to learn the algorithm, so I can execute it fully in my brain.

Right now, since the algorithm only has an accuracy of 70%, it?s still very bad at chess. I played a game, blindly using the algorithm, against Magnus Age 7 within the Play Magnus app, and I was very quickly defeated.

Still, it?s an exciting milestone: I finally have all the pieces I need to actually play algorithmic chess (i.e. Max Chess). Now, I just need to improve the algorithm itself?

Today is the 365th day of my M2M project and this is the 365th consecutive blog post. In other words, I?ve been M2Ming for exactly a year now, which is a crazy thing to think about.

In fact, it?s hard to remember what life was like pre-M2M, when I didn?t need to write a blog post every day. This blogging thing has just become a natural, expected part of my daily routine.

At the outset of this project, today was supposed to be the last day. Tomorrow, I?d wake up and the project would be over.

But, that?s not quite what?s happening?

As explained on October 1, I?ve extended this month?s challenge into November for reasons that I?m excited to share very soon.

Originally, I said that I would finish on November 9, but it?s looking like I may continue blogging until November 17 or so.

As I previously mentioned, I?d prefer not to deviate from the strict, one-month timeline (and just complete the project today), but these extra couple of weeks will be worth it.

I still can?t say too much more about why these extra couple weeks will be special, but it will all become clear soon.

A few days ago, after waiting eight hours for my personal computer to run my chess program, I found out that I would need more computing power to have any chance of creating a usable chess algorithm.

In particular, I can?t use my personal computer to process the amount of data I need to build my chess algorithm within a reasonable timespan. I need a much much faster, more powerful computer.

Luckily, cloud computing exists, where I just upload my code to someone else?s computer (Amazon?s, Google?s, etc.) through the internet, and then let their specially optimized machines go to town.

If only it were that simple though?

I spent some time trying to get my code running on Amazon Web Services, with limited success. After the basic setup, I struggled to get my massive dataset into Amazon storage to be accessed at code runtime.

But then, while researching my options, I came across a tool called Floyd, and it?s pure magic.

Floyd is a layer that sits on top of AWS and lets me deploy my code super easily:

1. I open Terminal, and navigate to my chess-ai folder on my local computer
2. I run two special Floyd commands
3. My code is uploaded to Floyd?s servers and instantly starts running on their GPU-optimized computers.

There are few additional things I needed to figure out like separately uploading and ?mounting? my dataset, downloading output files off of Floyd?s servers, etc.

But, overall, I got things up and running very quickly.

As a result, here?s my model running now?

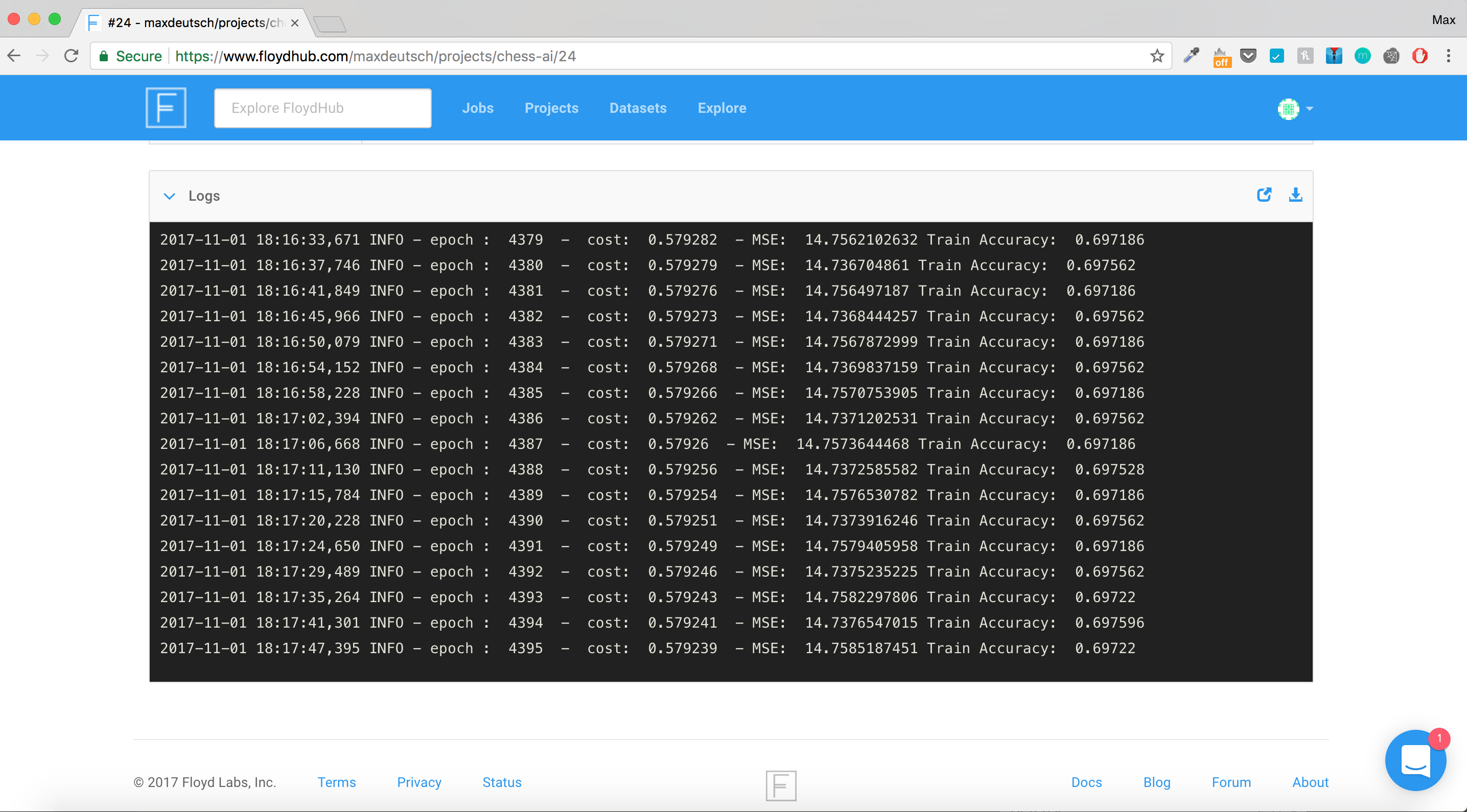
The Floyd computers seem about 3x faster than my personal computer, and I can run multiple jobs in parallel, so it?s definitely helping. Floyd runs at about 75% of the speed of AWS, but the ease of use more than makes up for this. It?s also only $99/mo for the biggest plan, which I?ll happily pay for something this good.

It?s always great to find a new tool that I can add to my arsenal.

Now, whenever I need to do any kind of data science or machine learning project in the future, I?ll know where and how to deploy it in only a few minutes.

This is why learning compounds over time? Today, I did a lot of upfront work to discover the best tool and learn how to use it. Now, I can continue reaping the rewards forever.

I might have a problem?

Yesterday, I excitingly found an easy way to get my chess code running on faster computers in the cloud. The hope was that, if I can process a lot more data and then train my model on this larger dataset, for more iterations, I should be able to greatly improve the performance of my chess algorithm.

As of a few days ago, I could only get my algorithm to correctly label a chess position as ?good? or ?bad? 70% of the time. I figured I could get this up to around 98?99% just by scaling up my operation.

However, after running the beefier version of my program overnight, I woke up to find that the algorithm is still stuck at the 70% accuracy level.

Not only that, but after it reached this point, the model continued to slowly improve its accuracy on the training data, but started to perform worse on the testing data.

In other words, after my algorithm reached the 70% mark, any attempt it made to improve actually caused it to get worse?

For example, after 6,600 iterations, the test accuracy was 68.1%:

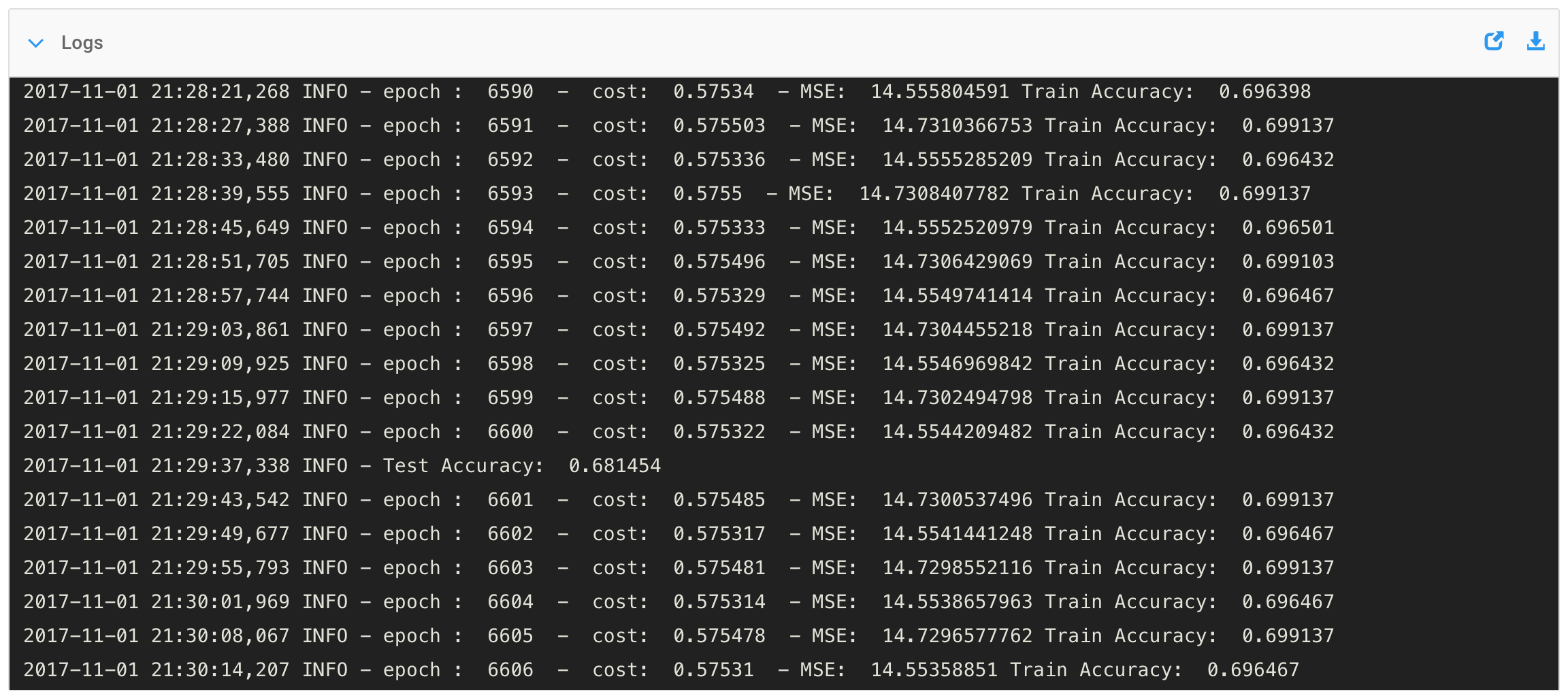
After 9,900 iterations, the test accuracy was down to 67.6%:

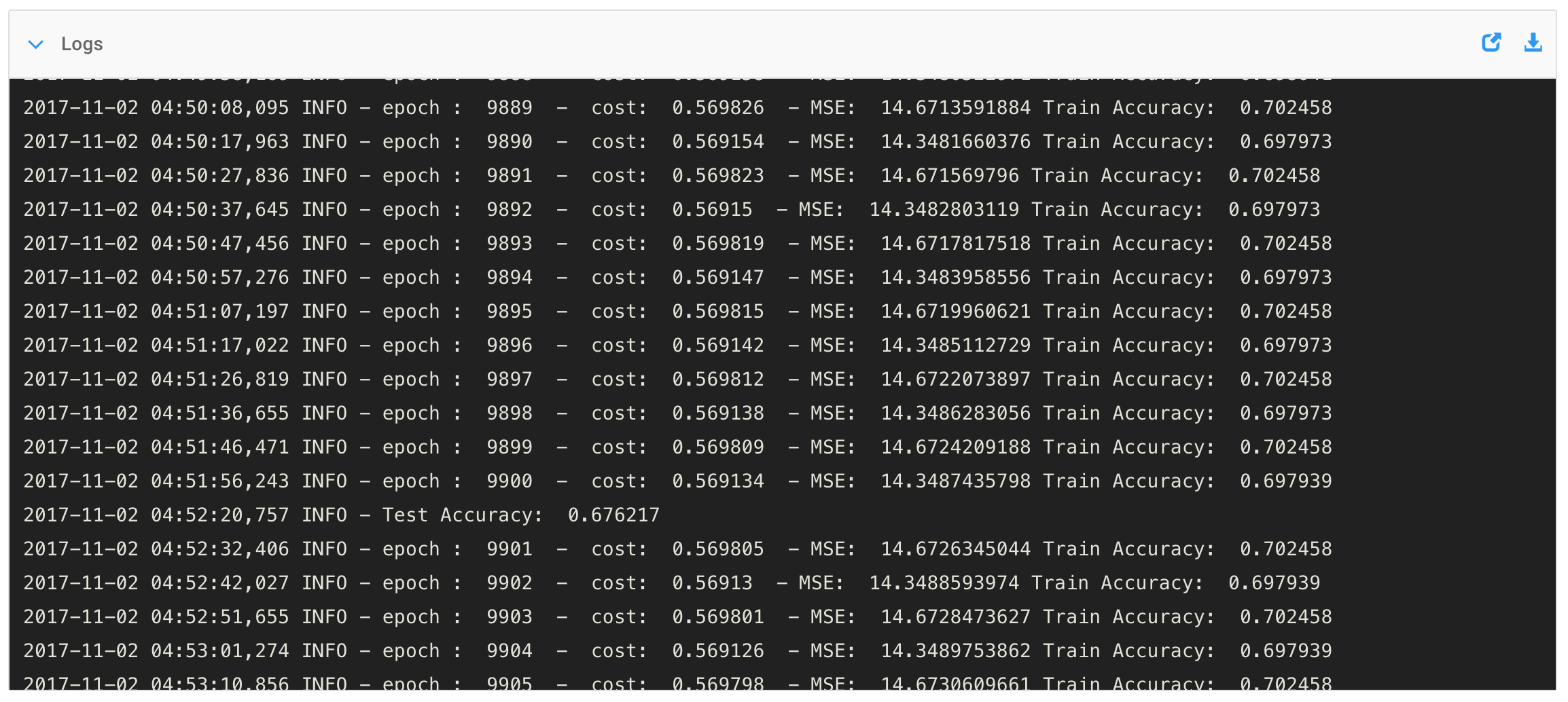
So, it seems that my model, as it?s currently constructed, is maxing out at 70%, which isn?t great. In fact, I?d bet the reason it plateaus here is fairly simple: 70% of the data in the dataset is labeled as ?good? and the rest is labeled as ?bad?.

In other words, my model performs best simply by guessing that every single chess position is ?good?, thereby automatically achieving 70% accuracy.

I haven?t confirmed this explanation, but I suspect it?s something like this.

So, now what?

Well, I was really hoping that I could use the most operationally-basic machine learning model, at a large enough scale, to pull this off. But, either the model isn?t sophisticated enough or my labelling scheme for the data is just nonsensical.

In either case, I have some ideas for how to move forward from here, which I?ll discuss tomorrow.

Yesterday, I ran into a bit of a problem: My chess program, as it currently exists, won?t be able to help me become a grandmaster. Instead, it will only help me correctly identify chess moves as ?good? or ?bad? 70% of the time, which is worse than I can do as an amateur human chess player.

So, if I want to have any shot of defeating Magnus, I need to try something else. In particular, I can either continue searching for an effective algorithm or I can try to find a completely new approach.

Before trying something new, I think it?s certainly worth continuing down the algorithmic path. After all, the failure of this one particular algorithm doesn?t imply that the entire general approach is hopeless.

In fact, I would have been extraordinarily lucky (or clever??) if the first algorithm (or class of algorithms) I tried was a functional one. Most often, when trying to create new technical solutions, it takes a few iterations, or more, to land at a workable solution.

Of course, these aren?t random iterations. I still need to be smart about what I try next?

So, what should I try next?

Within the algorithmic space, there are only two possible paths I can go down, and they aren?t exactly mutually exclusive:

1. Build a better model

Use the same dataset, but build a more robust model using Convolutional Neural Nets. Start with a highly sophisticated model, even if it?s not reasonable for human execution, just to see if a high-performance algorithm can even be made. If it can, then slowly reduce the sophistication of the model until it performs just at the level of Magnus Carlsen, and hope that this (or some optimized version of this) is learnable and executable by a human. If it can?t, then it means that my dataset is crappy, and I need to try option #2

2. Build a better dataset

Create a new dataset, constructed and labelled based on some new principle. In particular, try to use the fact that I?m human to my advantage. Maybe, construct the dataset based on a set of heuristics (i.e. for each piece: the number of other pieces directly attacking it, the number of other pieces able to attack it within one move, the number of possible moves it can make, the relative value of the piece compared to the other pieces on the board, etc.). Develop a long list of possible heuristics, and then use the computer to help find which ones are useful and in what combination (this is effectively what the convolutional neural net, from #1, should do, but it will likely be impossible to unravel what heuristics it?s actually using). Alternatively, use the same kind of board input, but label the outputs differently. Perhaps, for example, only try to output which piece is the best to move in each position.

Here?s my plan for moving forward:

1. Construct a Convolutional Neural Net, and run my current dataset through it.
2. In this way, either validate or invalidate the goodness of my dataset.
3. Assuming (very strongly so) that the problem is with my dataset, construct a new dataset, and run it through the Convolutional Neural Net.
4. Continue this process until I find a dataset that is good.
5. Then, start stripping back the model (i.e. the Convolutional Neural Net) while trying to maintain the performance.
6. If the model can be reduced, so that it can be performed by a human, without overly compromising the performance, ride off into the sunset (and by that I mean? spend a ridiculous amount of time and brainpower learning and practicing the resulting algorithm).
7. If the model cannot be reduced without sacrificing performance, try to find another good dataset.

Honestly, this whole process is quite thrilling. In a different life, maybe I would turn this into a Ph.D. thesis, where I try to algorithmically solve chess and then generalize these findings to other domains (i.e. How to develop computer-created, human-executable decision-making algorithms).

But, for now, the Ph.D. will have to wait, and instead, I?ll see what I can accomplish in an hour per day over the next few days.

I have good news and bad news?

The good news is that I?m much more proficient at building, training, and deploying machine learning models. Today, in only 30 minutes, I was able to construct a brand new, more sophisticated machine learning model (a convolutional neural network) based around my chess data, upload the dataset and model to a cloud computer (via Floyd), and begin training the model on machine learning-optimized GPUs.

The bad new is that it doesn?t seem like this model is going to perform any better than my previous one. In other words, as anticipated, the problem with my chess algorithm is a function of how I?ve constructed my dataset.

The new model is still training, so I could wake up to a surprise, but I?m not counting on it.

With that said, it is interesting how much more quickly I?m able to build and deploy new machine learning code. In fact, everything I?ve done for this month?s challenge I could now likely complete in one day.

That?s the amazing and crazy thing about learning? By fighting through the unknown and the occasional frustration, something that previously took me 30 days now will only take me a few hours.

Even if I don?t succeed at defeating Magnus at a game of chess in the next few weeks, I?ve definitely leveled up my data science skills in a big way, which will serve me very well in the future on a number of project.

This entire month?s challenge has hinged on a single question:

If I have a big set of chess positions labelled as either ?good? or ?bad?, can I create a function that correctly maps the numerical representations of these chess positions to the appropriate label with a very high degree of accuracy?

I think the answer to this question is yes, but it assumes that the original dataset is properly labelled. In other words, if I?ve incorrectly labelled some chess positions as ?good? when they are actually ?bad? and some as ?bad? when they are actually ?good?, my function won?t be able to find and correctly extrapolate patterns.

I?m almost certain that this is the current problem I?m facing and that I?ve mislabelled much of my dataset.

Let me explain where I went wrong (and then share how I?m going to fix it)?

Labelling my dataset v1

The dataset I?ve been using was labelled in the following way:

1. For a given chess position, compute its evaluation.
2. Then, for this given position, compute the evaluation of the position that came immediately before it.
3. Find the difference between the evaluations (i.e. the current evaluation minus the previous evaluation).
4. If this difference is greater than a certain threshold value, label the position as ?good?. If the difference is less than the same threshold value, label the position as ?bad?.

This method assumes that if the most recent move you made reduced the evaluation of the position, it was a bad move. Therefore, if you are evaluating this position, you should consider it bad because the move that got you there was also bad. (The same logic applies for good positions).

But, there is a problem here? There are multiple ways to reach any given position. And, the moves that immediately lead to this position don?t necessarily need to be all ?good? or ?bad?.

For example, in one case, I can play a sequence of all good moves, followed by one bad move, and end up in the ?bad? position. In another case, I can start the game by making bad moves, followed by a series of good moves (in an attempt to work out of the mess I created), and still end up in the same position.

In other words, it?s highly likely that, in my dataset, there are multiple copies of the same chess position with different labels.

If this is the case, it?s no surprise that I couldn?t find a reasonable function to describe the data.

Originally, I overlooked this problem via the following justification:

Sure, there might be multiple ways to get to a single chess position, but because I?m going to be using the algorithm for every move of the game, I will only be making a sequence of ?good? moves prior to the final move in the sequence. Thus, the evaluation of a given chess position will only be based on this final move ? where if the move is ?good?, then the chess position is naturally good and if the move is ?bad?, then the chess position itself is bad.

Even though this is how I would implement my chess algorithm in practice, my dataset was still created with all possible paths to a given chess position, not just the one path that I would take during game time.

And so, I essentially created a crappy dataset, resulting in a crappy machine learning model and an ineffective chess algorithm.

Labelling my dataset v2

An hour ago, I came up with a much better (and computationally faster) way to label my dataset. Here?s how it works:

1. Load a bunch of chess games.
2. For each game, determine if White won or lost.
3. For each chess position in each game, label all the positions as either +1 if White won the game and -1 if White lost the game (and 0 if it?s a tie).
4. Process millions of games in this way, and keep a running tally for each distinct position (i.e. If the position has never been seen before, add it to the list. If the position has already been seen, increment the totalassociated with the position by either +1 or -1).
5. Once all the games are processed, go through each of the distinct positions, and label the position as ?good? if its tally is greater than or equal to zero, and ?bad? if its tally is less than zero.

In this way, every chess position has a unique label. And each label should be highly accurate based on the following two thoughts: ?Over millions of games, this chess position led to more wins than losses, so it?s almost certainly a good chess position? and ?Over millions of games, this chess position led to more losses than wins, so it?s almost certainly a bad chess position?.

Additionally, because I don?t need to use the Stockfish engine to evaluate any of the moves, my new create_data program runs about 10000x faster than my previous program, so I?ll be able to prepare much more data (It processes 1,000 chess games, or about 40,000 chess positions, every 15 seconds).

Right now, I have it set up to process 2 million games or about 80 million chess positions overnight.

It?s been running for 30 minutes now and has already processed 193,658 games.

Honestly, this morning I wasn?t sure how or if I was going to make forward progress, but I feel really optimistic about this new approach.

In fact, I can?t see how this data wouldn?t be clean (so if you have any ideas, leave a comment and let me know).

Assuming this data is clean though, I should be able to generate a workable chess algorithm. Whether or not this chess algorithm will be human-learnable is another story. But, I?m going to take this one step at a time?

Last night, I left my computer running while it processed chess games using my new labelling method from yesterday.

As a reminder, this new method labels all chess positions from a winning game as +1 and all chess positions from a losing game as -1. Then, each time the program sees the same chess position, it continues to add together these +1 and -1 labels until a final total is reached. The higher the number, the more definitively ?good? the move is, and the lower the number, the move definitively ?bad? the move is.

After waking up this morning, I saw that my program had crashed after processing around 700,000 chess games. Simply, my computer ran out of usable memory.

Sadly, as a result, none of the output was saved.

Thus, I restarted the program, setting the cutoff to around 700,000 games.

Once the dataset was successfully created, I uploaded it to Floyd (the cloud computing platform I use), mounted it to my train_model program, and started training my machine learning model.

However, very quickly Floyd (which is just built on top of AWS) also ran out of memory and threw an error message. I tried to max out the specs on Floyd and rerun the program, but only to run out of memory again.

So, I scaled things back and created a dataset based on 100,000 chess games? This still broke Floyd.

I scaled back to 25,000 chess games, and finally Floyd had enough memory capacity to handle the training.

I?ve been running the training program for about four hours now and the accuracy of the program has been steadily climbing, but it still has a long way to go:

It started at around 45.5% accuracy on the test data (worse than randomly guessing, assuming good and bad positions are about equal).

And, after four hours, reached about 54.4% accuracy on the test data (slightly better than randomly guessing)?

Hopefully, if I let this program run through the night, it will continue to steadily march up towards 99%. (The program is only cycling through ~400 iterations per hour, so this could take a long time).

To hedge, I?m preparing a few other datasets that I also want to use for training purposes in parallel. In particular, I?m worried that, because I had to shrink down my dataset to get the program to run on Floyd, there may be many chess positions in my dataset that were only processed once, effectively labelled randomly (rather than being properly labelled by the aggregate view).

Thus, I?m creating a few datasets where I?m processing significantly more chess games, but only accepting chess positions into my labelled dataset that have been seen multiple times and demonstrate a definitive label (i.e. the chess position has a tally that is >25, or >50, or >100).

In this way, I can likely eliminate any one-off positions and create a dataset that has a cleaner divide between ?good? positions and ?bad? positions.

I also always have the option of introducing a third label called ?neutral? that is assigned to these less definitive chess positions, but an additional label will add significantly more complexity ? so it?s only worth it if it greatly increase the effectiveness of the algorithm.

Anyway, today has been a lot of waiting around, running out of memory, and crunching data. Hopefully, tomorrow, I?ll have some indication whether or not I?m headed in the right direction.

Honestly, this is starting to seem like a job for Google?s Alpha Go or IBM Watson as far as infrastructure and optimization are concerned. Is it too late in the game to pursue some kind of sponsorship/collaboration??

In a few hours, I get on a plane to Germany. I?ll be there until the 10th, and then will be in Denmark through the 12th.

In other words, I?ll mostly be traveling for the rest of this challenge.

I could of course stay in my hotel room and continue working on my chess code, but exploring these new countries is a much better use of my time.

So, let?s take stock of where I currently am?

Last night, I started running a new program that looked promising. However, almost immediately after publishing yesterday?s post, and after 4.5 hours of processing, the program failed: File sizes once again got too big, and this time, it seems like it had nothing to do with my infrastructure configuration, and instead, had to do with the limits of Python and Tensorflow.

Clearly, there?s some kind of optimization I?m overlooking.

This morning, I set up a bunch of other experiments, slicing and dicing the dataset in all sorts of ways.

I?m starting to get quite proficient at setting up new machine learning experiments (and also just conceptualizing new, useful experiments to run). However, even though I?ve made major progress on the software front, my hardware skills are still very raw, and I have a lot to learn about setting up the infrastructure necessary to successfully use large datasets and models.

I?m not sure I?ll have the time in Europe to address these hardware skill deficiencies.

Nevertheless, while my trip to Europe may slow down my chess code progress, it is still a continuation of this challenge?s narrative. I?ll explain soon?

I got to Germany today at around 6pm, so most of my day was spent attempting to sleep on an airplane.

However, while in the air, one of my machine learning models continued to train.

Yesterday, at 10am, when the model started running, it could correctly identify chess positions as ?good? or ?bad? with 68% accuracy:

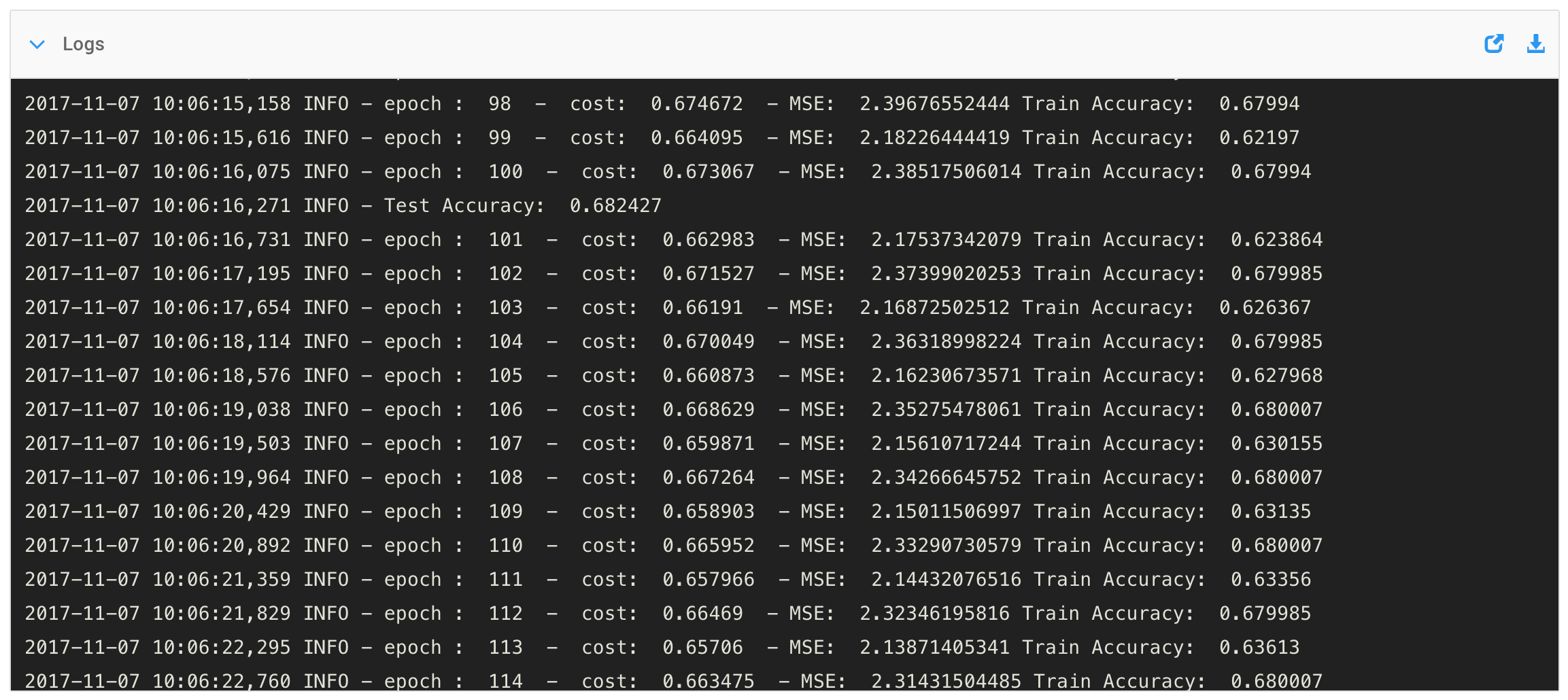
As of a few minutes ago, the model is now at 75% accuracy:

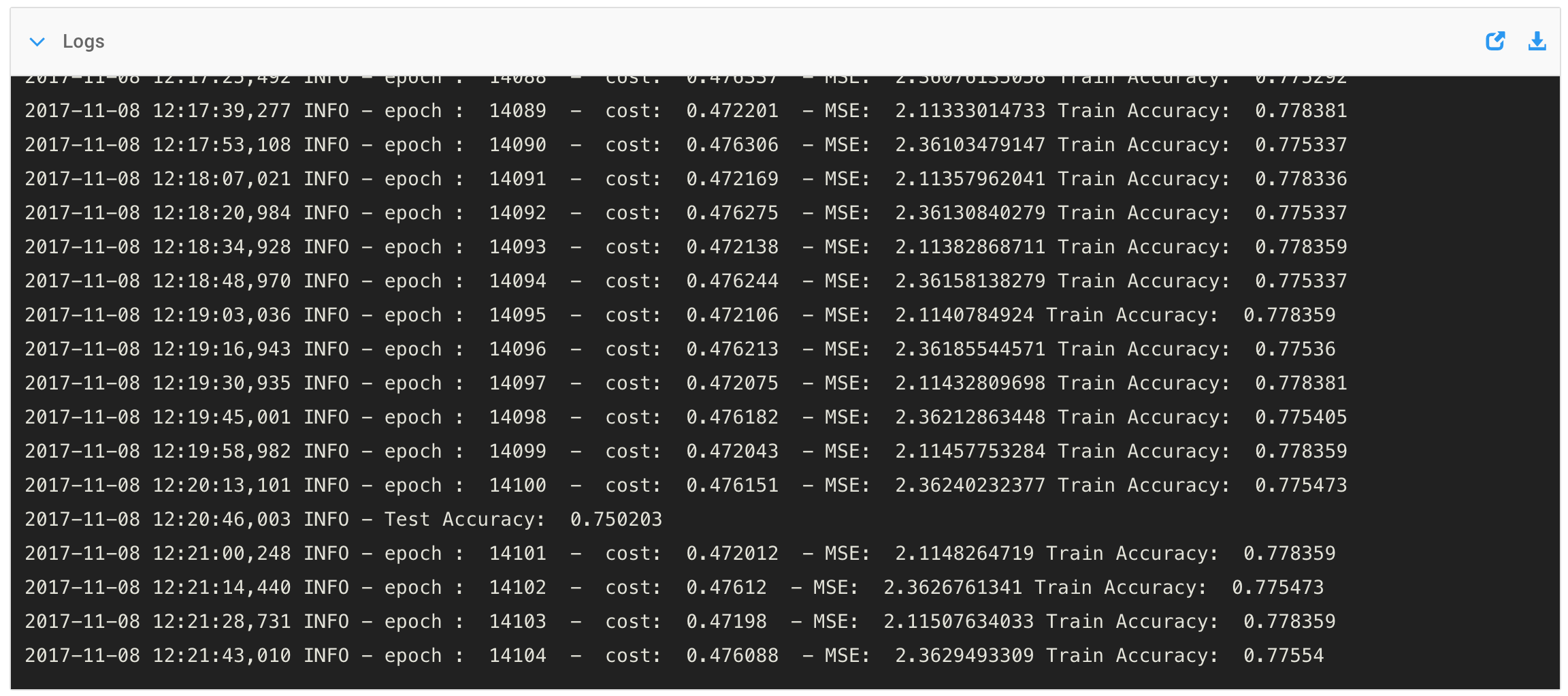
While there is still a long way to go, this is the most promising training session I?ve run to date: With each set of 100 iterations, the model?s accuracy is getting better and better with no sign of tapering off.

The progress is gradual, but steady.

This model might just go all the way?

I?m heading to bed now, but am eager to see its progress when I wake up.

Today, my computer was still chugging along, slowly training my machine learning model, which will ultimately, if successful, output my human chess algorithm.

This iteration of my model is still looking optimistic (as it did yesterday), but I couldn?t do much today other than wait for it to finish.

So, I figured today would be a good day to try to take on Magnus, Age 26, and see if I can win a chess game the old-fashioned way.

Of course, I haven?t exactly practiced much normal chess ? given that I committed heavily to my algorithmic approach ? but still, today, I gave a normal game my best go.

I started off playing solid for the first dozen moves or so, but eventually Magnus got an advantage?

Soon after, he leveraged this advantage and checkmated my King?.

Clearly, without an algorithm to lean on, Magnus is still dominant.

But, it?s not over yet? I still have a little time to get my algorithm up and running. I?ll let my computer keep chugging away, and hope it finishes up soon.

I?m typically very good at estimating how long doing anything will take me. Whether it?s writing a Medium post, or launching an app, or running errands, or practically anything else, I can usually guess the exact amount of time required plus or minus very little.

However, there are cases, particularly when I have limited experience in the relevant domain, when my time estimation skills fail me.

This month?s challenge is one of those cases?

I severely underestimated how much time I would need to allocate to training machine learning models. I expected (especially when using high-powered GPUs) that I could train any model in under a day.

However, this was a bad assumption: Currently, the model that I?m training (which is so far my most promising) has been running for over 80 hours and I suspect it will need at least another 80, if not even more, to finish.

In other words, the iteration cycle for something like this isn?t measured in hours, but rather weeks.

Typically, my learning method is to try something as fast as I can, see the result, react to the outcome, and iterate. But, this is a much more challenging approach to take when each iteration takes dozens of hours.

Coming into this challenge, I was fairly comfortable with the mathematical and theoretical parts of data science, but had limited practical experience.

During my self-driving car challenge, I became more comfortable with some of the basic tools, but didn?t actually have to do much real data science: For my self-driving car, I used an already-prepared dataset on an already-prepared machine learning model on an already-solved problem (more or less).

On the other hand, with this chess challenge, I needed to envision a new solution (to a new problem), prepare a new and useful dataset, and then build a new machine learning model specifically optimized for this dataset and my envisioned solution.

In other words, this time around, I needed to do everything from scratch, and, given that this was my very first experience with end-to-end data science, I had no reference point for how much time this would actually take.

Additionally, during the self-driving car month, I was able to run everything on my personal computer, not needing to learn about deployment in the cloud, as I did this time around.

Of course, when I started this chess challenge, I also didn?t anticipate that I would be leaning so heavily on data science in general, so I was really just hoping that ?whatever I come up with, it will be achievable in a month?.

Now that I feel more comfortable with practical, end-to-end data science, I could probably pull off the machine learning part of this challenge in a month or so, but it would still be really tough and I would need to get a little lucky (i.e. I still wouldn?t have time for many iterations).

And, even if I was able to complete the machine learning and data science parts of my algorithmic chess approach, I would still need to memorize and learn the algorithm in the remaining days of the month, which would also be quite tough: Learning this kind of algorithm would be similar to my card memorization challenge, but about 10x more involved.

In other words, I greatly underestimated how much time it would take to defeat the world chess champion. It turns out, not so surprisingly, that this is a pretty ambitious feat after all.

I?d say, more realistically, this challenge could be completed in about 3?6 months, starting from where I had started, working full-time at it.

Still, defeating the world?s best chess player after six months of preparations would be incredibly unprecedented and fascinating, so it still may be worth giving it a go.

The best part about incorrectly estimating the time required for anything is that you?re forced to reflect and recalibrate your time estimation abilities.

I?d say I have a much better sense of ?data science time? now, which I?m sure is something that will serve me well in the future.

Anyways, my model is still training, and I?m hoping that I can start playing around with the output by Monday or so.

Today, I spent most of the day exploring Copenhagen by foot. Although it was quite cold, it was a sunny day and I really enjoyed the city.

However, things didn?t go quite as planned?

I left the hotel this morning with a fully charged phone, but, for some reason, perhaps the cold, my phone immediately died after stepping outside.

Rather than heading back to the hotel, I figured I?d continue on without the crutch of Google Maps. I decided to just wander without a specific plan or direction, and then, at the end of my day, just try to find my way back.

I trusted that I?d figure it out.

There was something freeing about forging my own path and not relying on technology to guide me around. It forced me to be more present and to more fully observe my surroundings.

Interesting, this feeling of forging my own path is very similar to the one I experienced during this month?s chess challenge: I headed off into the unknown without a plan or a guide to follow, and found pleasure in the process of pioneering forward.

I eventually found my way back to the hotel, which I hope is a signal of what?s to come in these last few days of my chess challenge.

I just got off a twelve hour flight from Copenhagen back to San Francisco, so I?m going to keep this post pretty short?

While on the plane, since I had nothing better to do, I played around with my chess algorithm, trying to find ways to optimize it and ultimately finding a way to increase its efficiency by 10x.

In other words, my sloppy code was a large contributor to the slow training process over the past couple of days.

Anyway, with the boost in speed, my model is effectively done training now, and I?ve been using it to analyze and play chess games with promising results.

I?ll share more tomorrow?

Today, I finished the first version of my chess algorithm, allowing me to play a solid game of chess as a human chess computer. The algorithm is ~94% accurate, which may be sufficient.

Here?s a ten-minute video, where I explain the algorithm and use it to analyze a chess game on Chess.com that I recently played:

(Update: This is the game I played against Magnus, which I later revealed)

I?m excited that it works, and curious to see how much farther I can take it.

The next steps would be to determine the chess rating of the algorithm, play some assisted games with it to see how I do, and then, assuming it?s working as expected, see if I can optimize it further (to minimize the amount of required memorization).

It?s looking like Max Chess may actually become a reality?

Yesterday, I finally was able to test my chess algorithm on a recent game I played, and it worked quite well. You can watch the 10-minute video demonstration here.

Today, I dug a little bit deeper into the performance of the algorithm, and the results were still good, although not perfect.

For the first 25 moves or so of any chess game, the algorithm performs more or less perfectly. It identifies good moves as good and bad moves as bad ? comfortable carrying its user through the chess game?s opening and some of the middle game.

The algorithm performs less well in the late middle game and end game. In particular, during this part of the game, the algorithm?s threshold for good moves is too low: It recognizes too many inaccurate moves as good.

The algorithm does find the best line in the end games (consistently calculating these moves as good), but there is too much surrounding noise for me, as the user of the algorithm, to find this best line.

I?m not particular surprised by this outcome: This iteration of the model was only trained on 1,500 games and about 50,000 chess positions (I used this reduced dataset so that version 1 of my model could at least finish training before the challenge ended).

The problem with such a small dataset is that it likely doesn?t have enough duplicates of later-stage chess positions to produce accurate labels for these positions.

I just took a quick look at the dataset, and there are many later-stage chess positions that only appear once in the entire dataset. In fact, most of the later-stage chess positions only appear once, which distorts this part of the dataset.

On the other hand, the earlier chess positions are seen enough times that the true natures of these positions were correctly revealed when the dataset was created (Hence the nearly perfect results during openings and early middle games).

This problem can likely be remedied though: I just need to process many more games to create a fully undistorted dataset.

Of course, training a model on this dataset may take much longer, but the result, theoretically, should be significantly better for performance on all parts of the chess game.

Thus, today, I started training the same model, but this time on a dataset of 100,000 games. I?m also processing more games, hoping to build a dataset of around ten million games.

Based on what I?ve seen so far, I suspect these models, with the input of much more data, will be nearly perfect in their performance. After all, the current model is incredibly accurate, and it?s only basing its performance on 1,500 games.

If anything, yesterday?s result proved to me that algorithmic chess is a legitimate and functional approach (that already works reasonably well).

What is still unclear is whether or not ?perfect performance? at identifying good moves and bad moves leads to Magnus-level gameplay. This is still to be determined?

Two days ago, I showed that my algorithmic chess approach is actually workable. It?s still not quite finished, but it does and can work, which is quite exciting.

Right now, my computer is working away on V2 of the algorithm and it?s looking like the performance of this version is going to be better.

I?m going to officially end this challenge and the entire project on Friday, so I?m not sure I?ll be defeating Magnus at chess before then.

Even if I don?t complete this challenge in the next two days, the past six weeks have been particularly exciting for me:

1. I pioneered a new way to learn and play chess (and validated that it has potential), hopefully impacting the future of chess in some capacity.
2. I developed a much stronger practical understanding of the end-to-end data science and machine learning process, which will serve me very well moving forward.
3. I discovered a much deeper appreciation for the game of chess and for the ongoing dedication of the world?s top players to the game. I finally understand the beauty of the game, and will certainly continue playing chess the normal, non-algorithmic way reasonably regularly.
4. I made some interesting friends in the chess community, which I?ll talk more about on Friday.

Overall, a very successful ?unsuccessful? challenge.

In other words, while I might not succeed at reaching my particular goal (of defeating Magnus), I was successful in using this goal to propel myself into a new space, to find a new source of intellectual joy, and to flex my creative and technical muscles in pursuit of the goal.

This point is important: Don?t measure the quality of your life by the outcomes, but by the pursuit of those outcomes.

If you optimize for and value the pursuit, favorable outcomes will follow anyway, even if they aren?t the outcomes you planned for.

If you only value the outcomes, you will miss out on most of the pleasures of your life ? since we spend most (all) of our life in pursuit.

Like with all of my past challenges, today I decided to tally up the total amount of time I spent on this final chess challenge.

Since this challenge was effectively 50% longer than previous challenges, it?s no surprise that I spent a bit longer on it. In particular, over the past six weeks, I committed 34 hours to the pursuit of defeating Magnus.

It turns out that 34 hours isn?t quite enough, but, knowing what I know now, I don?t think it?s too far off.

I?d estimate that it would take between 500?1,000 hours to become a human chess computer capable of defeating the world champion (assuming that an algorithmic approach at this level of gameplay is possible? the verdict is still out).

While this is considerably more time than the 34 hours I spent, it?s completely dwarfed by the tens of thousands of hours that Magnus has spent playing chess.

Of course, this estimate only matters if I can actually demonstrate the result.

For now, I?m going to take a little break from my chess preparations, but, if inspiration strikes, I?m may proceed forward.

1,000 hours really isn?t so crazy. It?s about six months of a standard 9-to-5 job.

I suspect that I?ll be circling back some time in the future, putting in these 1,000 hours, and, assuming everything goes to plan, playing a competitive game against Magnus (in what will still likely be a very lengthy game).

Until then, Magnus can continue enjoying his spot at the top?

Today is the very last day of my M2M project, and I?m excited to finally share one of the most unexpected parts of this month?s challenge (and the entire project): I had the opportunity to play a game of chess, over the board, with the real Magnus Carlsen last week (November 9) in Hamburg, Germany.

It was an incredibly energizing and enjoyable experience, and I?m really grateful that I had the opportunity.

To celebrate the completion of the project, The Wall Street Journal wrote a story covering the match, and produced a video to go along with it:

FAQ 1: How did you set up a game with Magnus?

I didn?t. The game was offered to me (via a collaboration between Magnus?s team and the Wall Street Journal), and I accepted. This didn?t seem like something I should turn down.

FAQ 2: Did you actually think you were going to win?

I never thought I was going to win. In fact, this was the entire premise of this challenge: How could I take what is an impossible challenge (i.e. if I trained using a traditional chess approach, I would have an effectively 0% chance of victory), and approach it from a new angle. Perhaps, I wouldn?t completely crack the impossibility of the challenge, but maybe I could poke a few holes in it, making some fascinating headway and introducing some unconventional ideas along the way. This was more an exploration of how you approach the impossible than anything else.

While I made decent and interesting progress towards this alternative approach, it wasn?t quite ready by the time that I sat down for the game with Magnus. So, barely having learned normal chess, I sat down to play the game as a complete amateur.

Anyway, this year has been a ton of fun, and I?m sure M2M Season 2 is somewhere in my future.

Until then, thanks to everyone who has been following along, providing input, and supporting the project over the past twelve months. It has meant (and continues to mean) a lot to me.

This post is part of my year-long accelerated learning project, Month to Master.

Max Deutsch is the co-founder of Monthly ? an online education platform that partners with some of the world?s biggest YouTubers to create one-month, highly-immersive online classes.

For exclusive content on accelerated learning, discipline, and lifestyle design, subscribe to my once-in-a-while newsletter.