When it comes to 8-bit music, probably the first thought that comes to mind is the soundtrack of old videogame consoles. Currently, with a simple Youtube search on the topic, you can see countless versions of songs recreated with the timbre of these consoles in versions entitled as 8 bits. Throughout the years of study in acoustics and audio, some confusions regarding the theme were found by the author of this article, especially in environments aimed to enthusiasts of audio and games. This confusion can be summarized in a few main questions: does a song sound like a videogame soundtrack because it has 8 bits (or less) of resolution? If we record a real 8-bit instrument will it sound like one of the Super Mario World soundtracks? In order to have an answer, firstly, we have to understand the concept of digital audio, the meaning of bits and audio resolution.
Analog technology has gradually been replaced by digital in recent decades, and despite some resistant enthusiasts of these old devices, the digital media has raised the significance of technological advancement to another level.
The music industry also did not stuck in time, and gradually ceased using magnetic tapes and vinyl records to make room for A/D converters and storage on computers or smartphones.
 Examples of some audio analog and digital technology.
Examples of some audio analog and digital technology.
However, before turning into digital, the recorded signals come from some analog electrical signal generated by a transducer, such as a microphone or an electric guitar.
 The microphone transforms the sound energy into an analog electrical signal, measured in volts.
The microphone transforms the sound energy into an analog electrical signal, measured in volts.
The analog electric signal has by its intrinsic characteristic to be continuous, in other words, it is formed by infinite points. This means that it has information at any points along its length. Under these conditions, would a computer be able to store an analog signal? No, because having infinite points of data would not allow even a single song to be stored! Then, as a solution, some points of data are periodically sampled, according to the sampling frequency of the A/D converter.
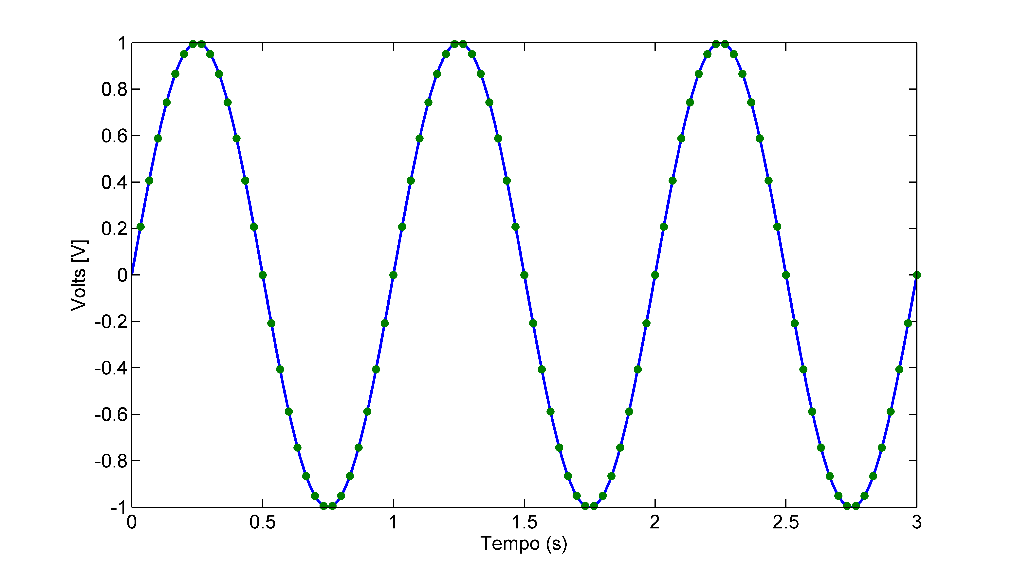 Sampling frequency in time domain.
Sampling frequency in time domain.
The sampling frequency is, therefore, the number of samples that the digital signal has per second. A Compact Disc (CD), for example, has a sampling frequency of 44100 Hz, which means that in each second of reproduction there are 44100 samples of data.
And how does the computer understand the signal amplitude? That is what bits are made for. For each one of these data samples, a corresponding bit number will be assigned conforming its amplitude, and according to the bit depth (number of bits available) of the A/D converter.
The bits are binary numbers, which can be only two values: ?0? or ?1?, and it is the basic storage unit of the computer. Bit sequences can represent a decimal number or a word, as shown below:
 Computer reads bits at very high speed
Computer reads bits at very high speed
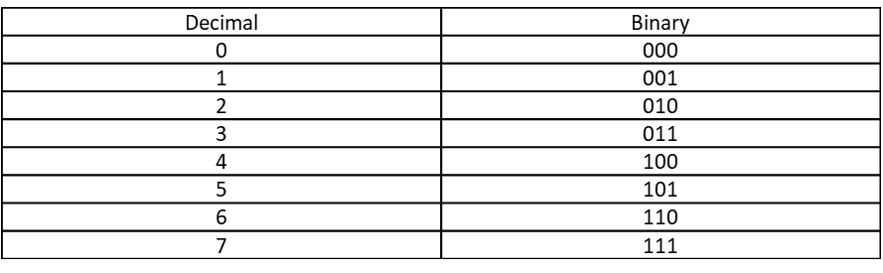
Each decimal number can be converted to a corresponding binary. For 3 bits quantization, for example, we have the possibilities as shown in the table.
A 3 bits quantization can generate 8 different possibilities of amplitudes, while 16 bits can generate 65536 possibilities. The image below represents a 4 bits quantization.
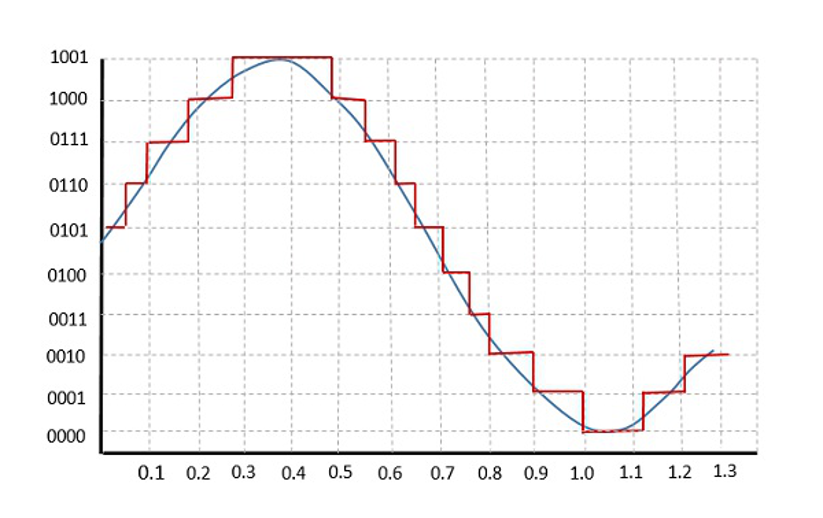 Representation of the analog signal and the digital one quantized in 4 bits.
Representation of the analog signal and the digital one quantized in 4 bits.
Once understood the concepts of bits and its effects on the waveform, we can introduce now its relationship with audio from games.
The old consoles have soundtracks whose timbre is remarkable, referring immediately to the games of the time. Raising again the initial question of the article: why do these soundtracks sound like this? Is it because it has 8-bit resolution?
The reader can draw their conclusions gradually by listening to the audios of a guitar record below, first recorded in 16 bits:
Reducing it to 8 bits:
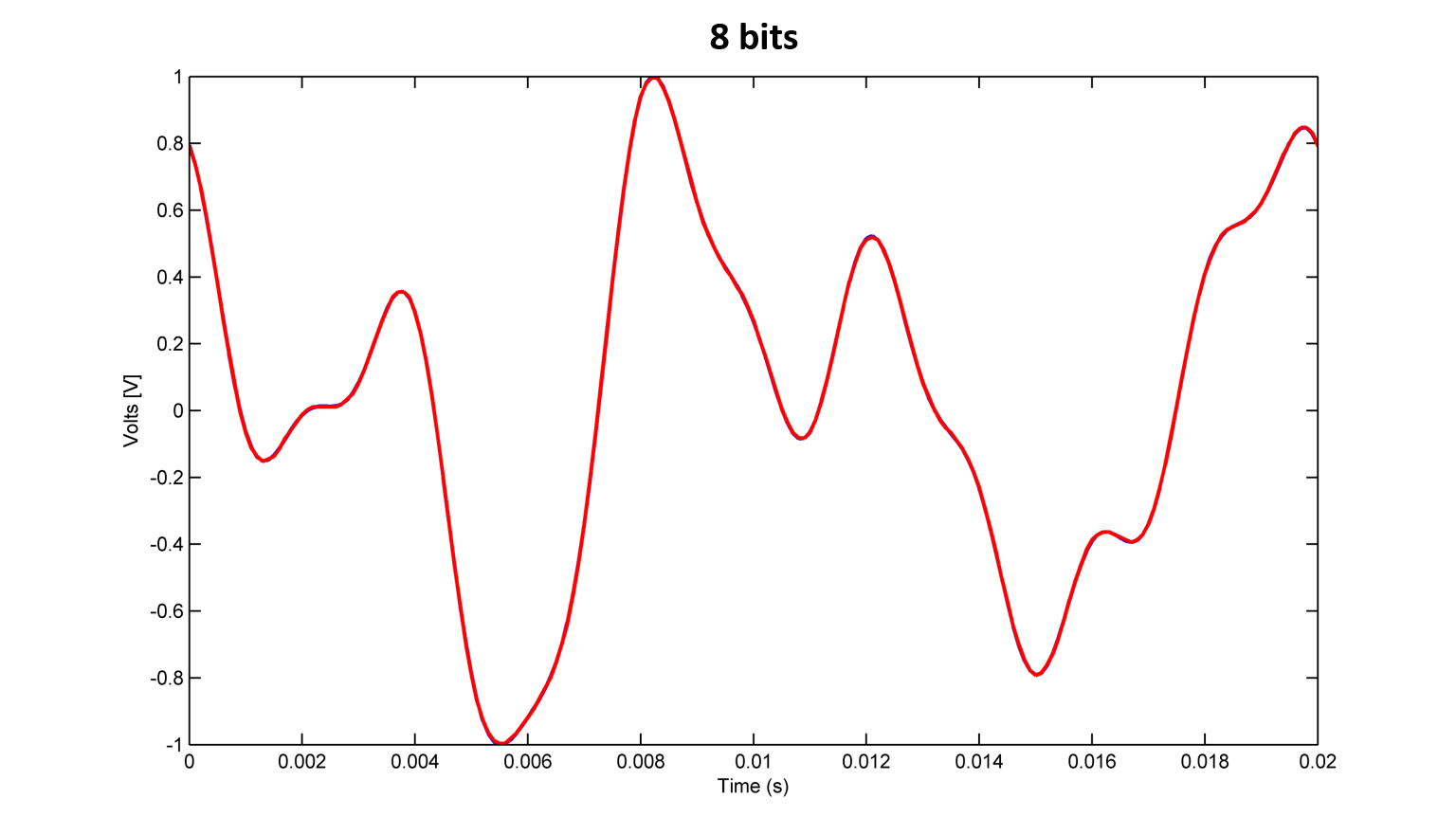
The 8-bit signal has its waveform almost exactly the same as the original, and also sounds very identical.
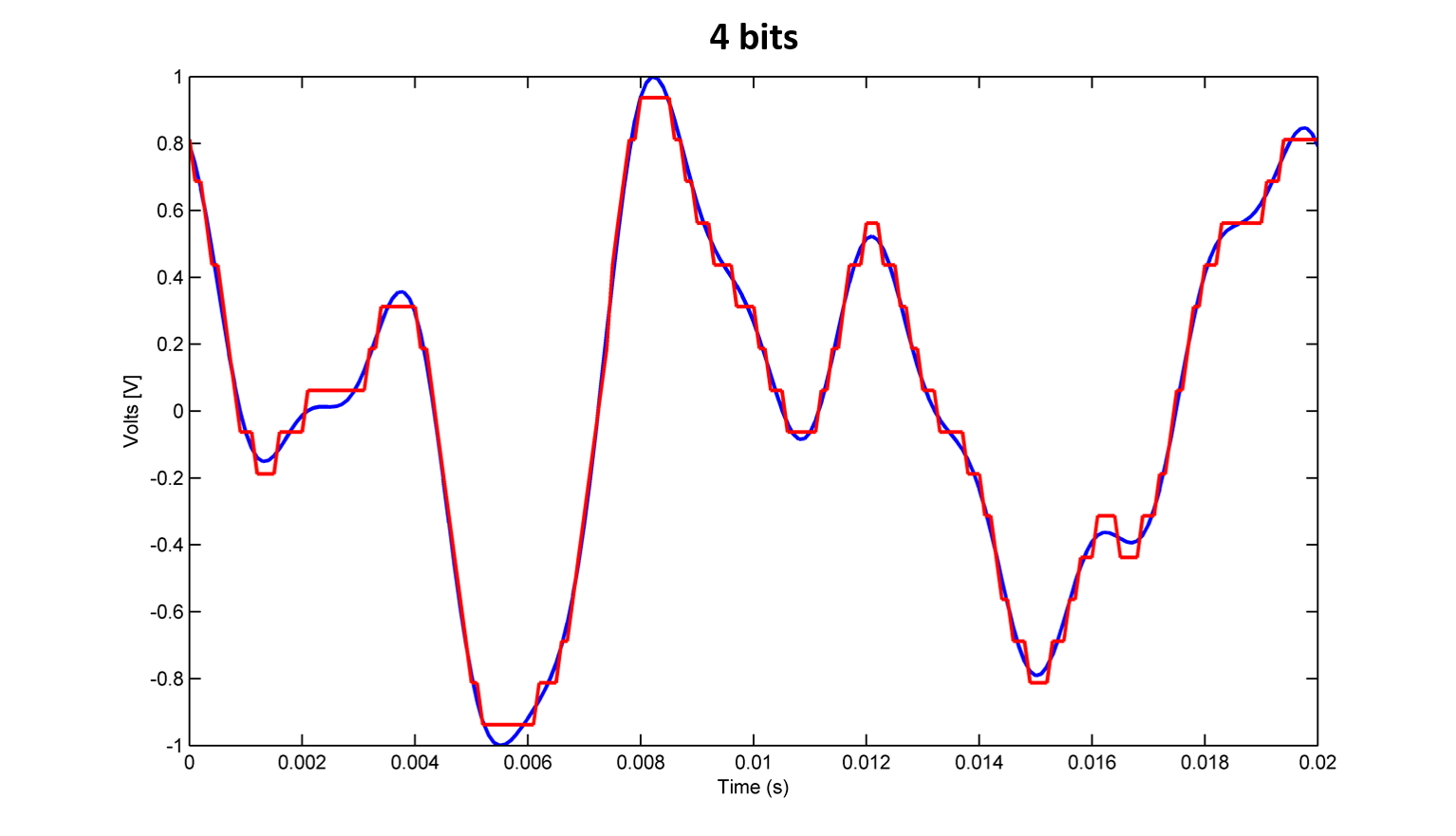
Now, in 4 bits, the difference becomes evident.
The signal assumes a squarer waveform.
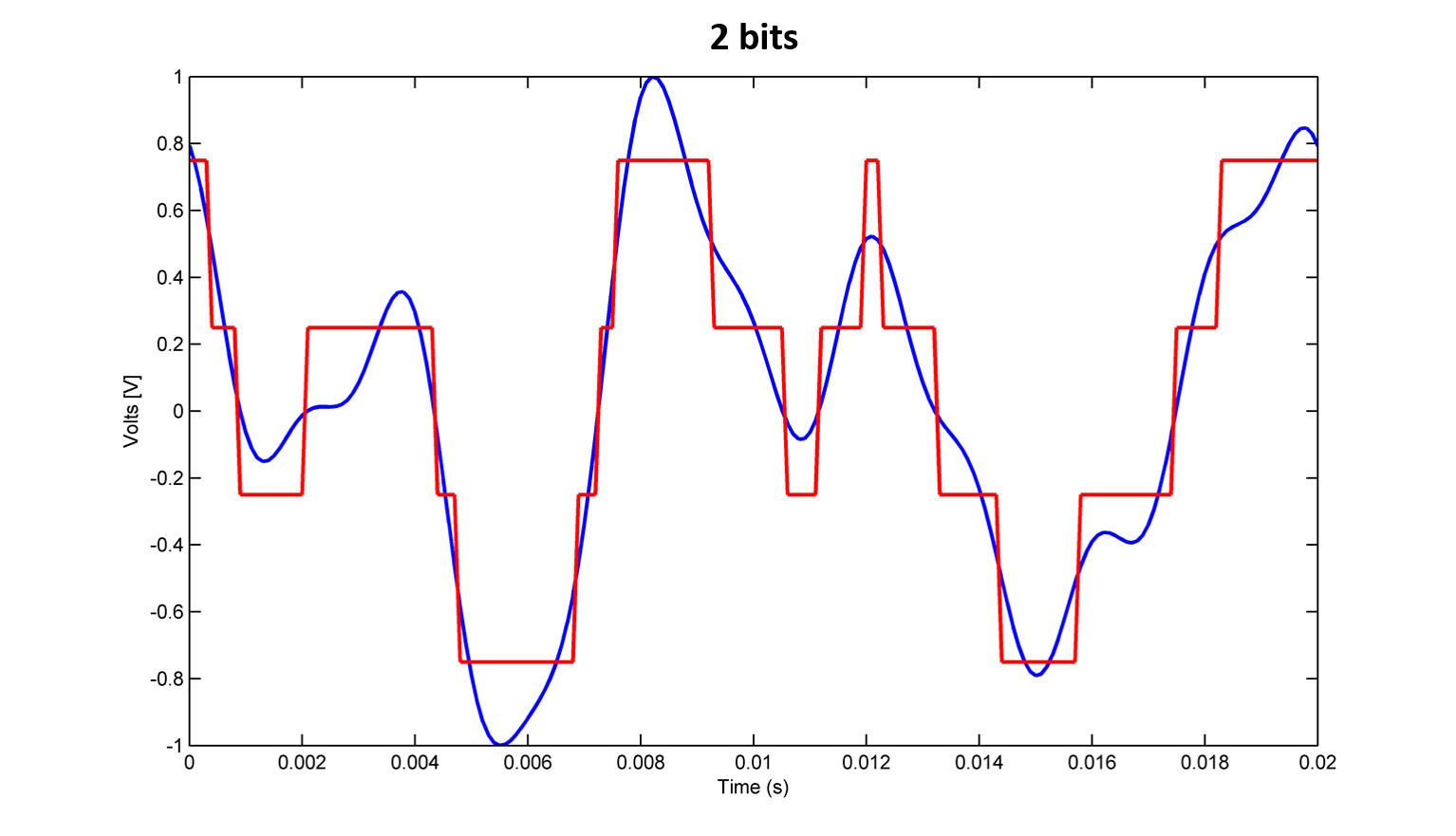
2 bits!
And, finally, 1 bit!
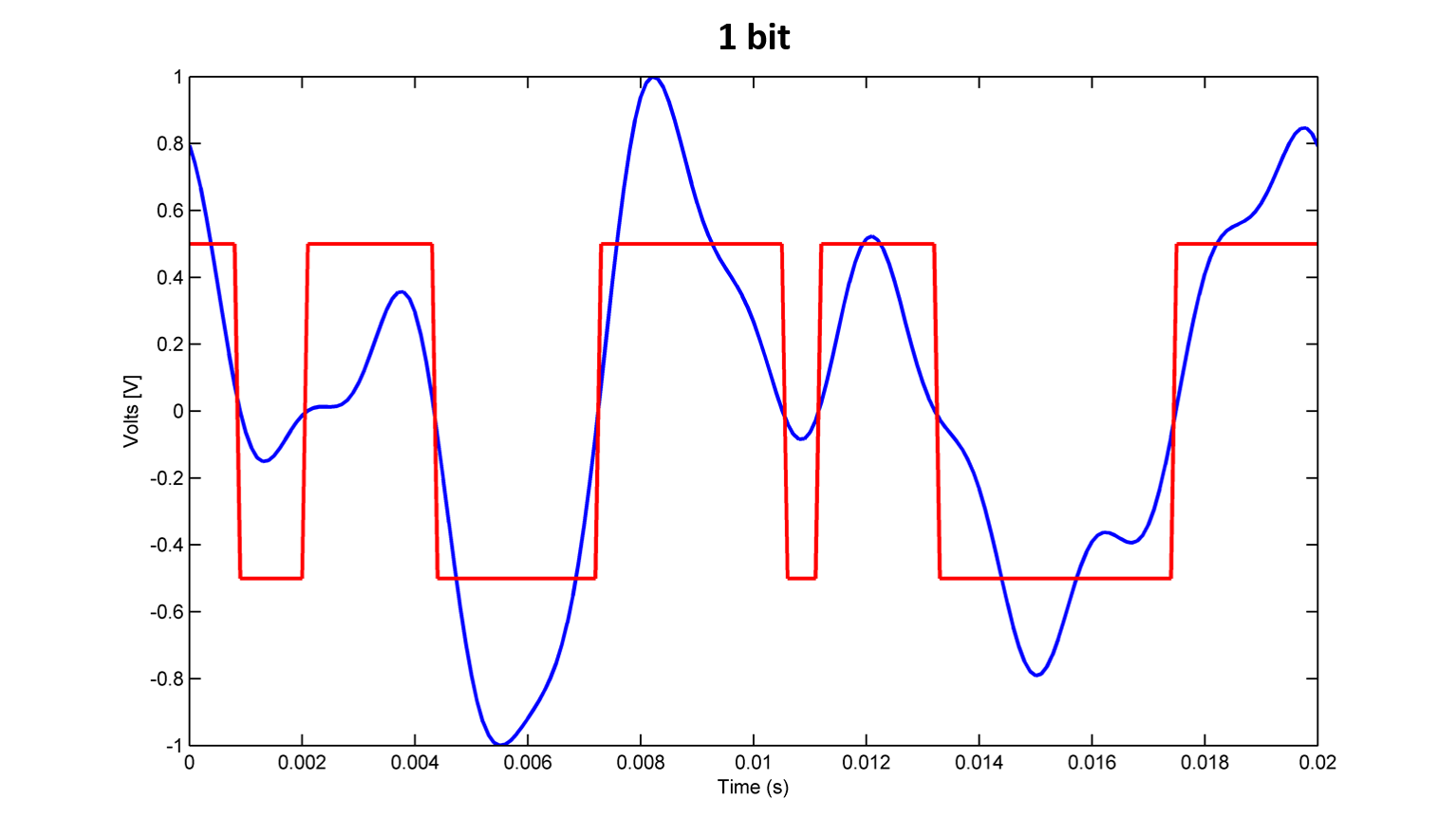
At this point in the article any reader should have noticed that reducing the number of bits added more noise and distortions to the signal, but in neither of the examples above it sounded like the timbre of a videogame. In the 8-bit example, the difference is so small that possibly no one notices difference to the original audio using simple reproducing devices.
Below 4 bits nothing interesting happens apart from adding a plenty of distortion to the signal, making it almost unbearable to listen to.
In the end, what generated the classic timbre of our old consoles was the fact that their soundtracks were made on triangular and square wave synths of their chiptunes, and so they sounded on that way because of the characteristic timbre of these waveforms. Therefore, there is no relation with the number of bits from the audio, which would sound exactly the same if played at high resolutions such as 16 or 24 bits.
The distortions that occur when decreasing the number of bits is due to the presence of square waves in the signal, which appear as the signal is ?cut? at its extreme points, leading to the generation of harmonic frequencies.
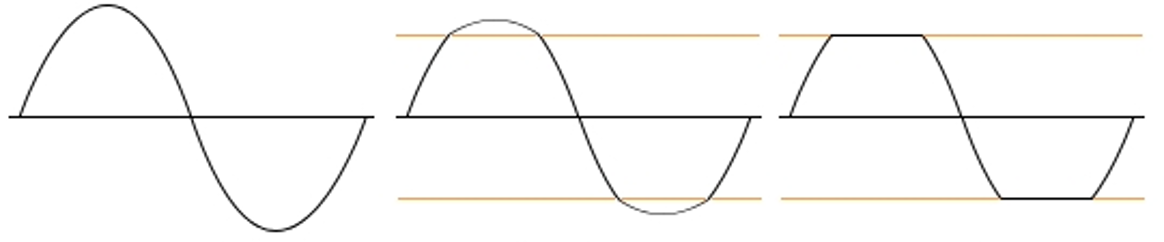 The signal saturation leads to distortions (harmonics)
The signal saturation leads to distortions (harmonics)
Some important points to keep in mind:
- The so-called 8-bit music, which are often a recreation of existing songs to sound computerized, do not sound that way because of the 8 bits. The reason is actually the form they were created.
- Real instruments when played in a quantization less than 8 bits will sound totally distorted, and not like a video game.
It might be a matter of naming, but it is necessary to be aware of the difference between 8-bit resolution and 8-bit musical style to not fall into erroneous technical interpretations.
www.harmonia.global
Marcel Pozzobon Borin | [email protected]


