7.1 Introduccin
El trmino conjunto es bastante primitivo y fundamental en toda la estructura matemtica. Generalmente, esta palabra se acepta en matemticas como un trmino indefinido, tal como en geometra que toma, entre otros, los trminos punto, lnea, plano, que sin definicin pero si de manera intuitiva. Similarmente sucede con el trmino elemento. La teora de conjuntos es una parte de las matemticas que tiene un objeto de estudio propio; con mtodos propios, con ciertas relaciones con otras teoras matemticas, en particular, con todas las teoras matemticas tradicionales y a partir de sus principios se mantiene la existencia, estructura y relaciones mutuas entre ellos. Es decir, que el resto de la matemtica puede expresarse en trminos de conjuntos. Georg Cantor (1845?1918) matemtico, fsico y filsofo alemn de origen ruso. Se doctor en 1867 y empez a trabajar como profesor adjunto en la Universidad de Halle. En 1874 public su primer trabajo sobre teora de conjuntos. Es considerado como el padre de ?la teora de conjuntos?. Cantor oper con conjuntos infinitos, transformando unos en otros mediante reglas precisas, los compar respecto a su cardinalidad y mostr cmo asignar un nmero cardinal a cada conjunto. Entre sus primeros resultados encontr que dos conjuntos tienen la misma cardinalidad, si tienen correspondencia biunvoca entre ellos. Si dos conjuntos no tienen la misma cardinalidad, pero tienen correspondencia biunvoca con un subconjunto de otro, la cardinalidad del primero es menor que la del segundo. Su mente luch contra varias paradojas de la teora de conjuntos, en otras la paradoja de Bertrand Russell, que parecan invalidar toda su teora; es decir, la haca inconsistente o contradictoria, en el sentido de que una cierta propiedad podra ser a la vez cierta y falsa. A fines de mayo de 1884 Cantor tuvo su primer ataque registrado de depresin. Se recuper despus de unas cuantas semanas, pero apareca menos confiado. En junio de 1917 ingres una institucin mental de Halle (ciudad del centro de Alemania) por ltima vez; de all le escriba continuamente a su esposa pidiendo que le permitiera regresar a casa. Muri en un ataque cardiaco, el 6 de enero de 1918, cuando tena 73 aos de edad.

7.2 Concepto de conjunto
Se llama conjunto a toda agrupacin, coleccin o reunin de individuos (cosas, animales, personas o nmeros) bien definidos que cumplen una propiedad determinada. A los objetos del conjunto se denominan ?elementos?.
Ejemplo 7.1: Los siguientes son algunos ejemplos de conjunto: . El conjunto formado por los colores de la bandera de Colombia.
. La coleccin de letras de la palabra ?murcilago?.
.El conjunto formado por los dgitos del nmero 345923238.
.La agrupacin de nmeros naturales menores que 10
.La agrupacin de nmeros primos entre 0 y 20.
7.3 Notacin de conjuntos

Ejemplo 7.2: utilice la notacin correcta para escribir los conjuntos dados en el ejemplo 7.1
A= El conjunto formado por los colores de la bandera de Colombia.
B= La coleccin de letras de la palabra ?murcilago?
C= El conjunto formado por los dgitos del nmero 345923238
D= La agrupacin de nmeros naturales menores que 10
E= La agrupacin de nmeros primos entre 0 y 20
7.4 Determinacin de conjuntos
La determinacin de un conjunto corresponde a la manera como ste puede expresarse. Para determinar un conjunto se utilizan dos formas: determinacin por extensin y la determinacin por comprensin.
7.4.1 Determinacin de conjuntos por extensin
Un conjunto se determina por extensin cuando se enumeran o se nombran los elementos del conjunto. Cuando el conjunto es finito se escriben entre llaves, separados por comas. Cuando el conjunto es infinito se escriben entre llaves algunos elementos y se ponen puntos suspensivos
Ejemplo 7.3: Determine por extensin los conjuntos del ejemplo 7.2
A={amarillo, azul, rojo}
B={m, u, r, c, i, e, l, a, g, o}
C={3,4,5,9,2,8}, no se repiten elementos
D={1, 2, 3, 4, 5, 6, 7, 8, 9}
E={1, 2, 3, 5, 7, 11, 13, 17, 19}
7.4.2 Determinacin de conjuntos por comprensin
Un conjunto se determina por comprensin enunciando la propiedad o cualidad que distingue a los elementos. Para tal fin se utiliza lo siguiente: {x/x cumple la propiedad}, que se lee: el conjunto de las x tal que x cumple la propiedad
Ejemplo 7.3: Determine por comprensin los conjuntos del ejemplo 7.2
A={x/ x es un color de la bandera de Colombia}
B={x/ x es una letra de la palabra ?murcilago?}
C={ x/ x es un dgito del nmero 345923238}
D={ x/ x es un nmero natural menor que 10}
E={ x/ x es nmero primo entre 0 y 20}
7.5 Representacin de conjuntos
Existen varias formas de representar los conjuntos: representacin grfica y representacin en la computadora.
7.5.1 Representacin grfica de conjuntos
Los conjuntos se pueden representar grficamente mediante diagramas de Venn y por diagramas de Caroll. Diagramas de Venn (figura 7.1). Estos diagramas fueron descubiertos por el lgico y matemtico britnico John Venn (1834?1923). El sistema de representacin que hoy conocemos fue desarrollado en julio de 1880 con la publicacin titulada ?De la representacin mecnica y diagramtica de proposiciones y razonamientos? en el Philosophical Magazine and Journal of Science, lo cual provoc cierto revuelo en el mundo de la lgica formal. Esta representacin ms conocida como ?diagramas de Venn?, consisten en figuras geomtricas planas y cerradas; dentro de cada figura se ponen los elementos que le corresponden. Estos diagramas sern los utilizados en el desarrollo de este texto.
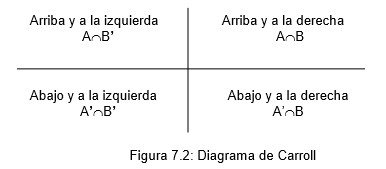
Diagramas de Carroll (figura 7.2). Son bastante tiles para el estudio de las propiedades de los complementos de conjuntos. Consisten en lneas perpendiculares que se cortan (una horizontal y otra perpendicular) tal que un plano cartesiano; en la parte superior e inferior de la lnea horizontal se ponen los elementos que cumplen una propiedad y de manera similar al lado izquierdo y derecho de la lnea vertical. De tal manera se pueden realizar las operaciones entre conjuntos.
7.5.2 Representacin de conjuntos en la computadora
Un conjunto se puede representar en la computadora como arreglo unidimensional de longitud n (n nmero de elementos de A) que en el argot de la computacin se denomina ?vector? y por lo tanto, se pueden realizar las operaciones que hacen con conjuntos: interseccin (datos repetidos de los vectores, eliminando los repetidos), unin (poniendo los elementos de los vectores, pero eliminando los repetidos) y as sucesivamente con la diferencia y el complemento. Este tema sen tratar al final de este captulo. Se recomienda para su estudio recordar los conceptos acerca del manejo de arreglos en computacin.
7.6 Relaciones de conjuntos
Las relaciones que se pueden dar entre conjuntos son: pertenencia, inclusin e igualdad.
7.6.1 Relacin de pertenencia
El signo que representa la relacin de pertenencia es E, que fue descubierto por el matemtico y filsofo italiano, Giuseppe Peano (1858 ?1932), quien es conocido por sus contribuciones a la Teora de conjuntos. En efecto, sea A un conjunto cualquiera y x un elemento, para indicar que x es elemento de A o simplemente que, x est en A se simboliza

ver en la seccin 6.9; tampoco se da entre elementos. Por lo tanto, es incorrecto escribir x E x o A E A

7.6.2 Relacin de Inclusin de conjuntos
Dados dos conjuntos A y B, esta relacin se utiliza para indicar que el conjunto A es subconjunto del conjunto B, lo cual se escribe:
![]()
y se lee: A es subconjunto de B, A est incluido en B, A est contenido en B, B incluye a A.

Si A es un subconjunto de B y existen elementos de B que no estn en A, entonces A es un subconjunto propio de B y se simboliza

7.6.3 Propiedades de la inclusin

Sus demostraciones son sencillas; basta con utilizar las propiedades las definiciones de inclusin y pertenencia, adems, de las propiedades de cuantificadores. En efecto veamos, x E A Por hiptesis

Ejemplo 7.5: dados los conjuntos A={3,5,6,9,4}, B={3,4,7,9,6,5} y C={3,9,5,7,4,6,8,} ponga entre el parntesis V o F si los siguientes enunciados son verdadero o falso, respectivamente y justifique el por qu de los falsos.

Segn el ejemplo se puede observar que A es subconjunto propio de B y a la vez ste de C.
7.6.4 Relacin de igualdad de conjuntos
La igualdad de dos conjuntos A y B denotada A=B
se da cuando todos los elementos de A estn en B y viceversa. Simblicamente,
![]()
Esta equivalencia se conoce como axioma de extensionalidad. La igualdad de conjuntos intuitivamente dice: ?dos conjuntos son iguales si y solo tienen los mismos elementos (no importa el orden)?. Tenga en cuenta que este concepto es diferente a decir: ?dos conjuntos son iguales si y solo tienen la misma cantidad de elementos?. Si algn elemento x de A no est en B o algn elemento x de B no est en A se dice que A es diferente de B y se simboliza
![]()
Ejemplo 7.6: dados los conjuntos A={x/x es un nmero primo positivo menor que 8},
B={ x/x es un factor de 210}
A=B? Comprubelo. A={2,3,5,7}
B={2,3,5,7} Luego, los conjuntos son iguales
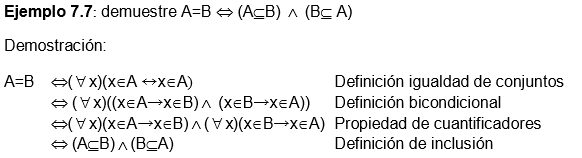
7.7 Clases de conjuntos
7.7.1 Conjunto finito
Es aquel conjunto cuya cantidad de elemento se puede contar; es decir, es aquel conjunto en que sus elementos se pueden nombrar o enumerar. Ejemplo 7.9: A={x/x es un nmero entero mayor o igual que -3 y menor que 5}. Este conjunto est formado por 8 elementos. En efecto, A={-3, -2, -1, 0, 1, 2, 3,4}
7.7.2 Conjunto vaco
Existe un conjunto especial denominado ?conjunto vaco? o ?conjunto nulo? y algunos definen como un conjunto sin elementos. Este ltimo concepto se presta para confusiones cuando se dice ?conjunto sin elementos?; pues se sabe que un conjunto es una agrupacin de objetos que cumplen una propiedad determinada. Esta confusin se aclara defiendo el conjunto vaco como aquel en que ningn elemento cumple con la propiedad conocida como ?regla de elegibilidad?.
![]()
No es correcto decir, ?un conjunto vaco?; debe decirse siempre ?el conjunto vaco? porque este conjunto es nico.
![]()
7.7.3 Propiedades del conjunto vaco
![]()
Ejemplo 7.10: los siguientes ejemplos ayudan a conceptualizar el conjunto vaco:
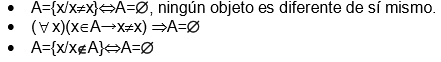
Esta regla es muy importante:
![]()
7.7.4 Conjunto unitario
El conjunto unitario es aquel solamente tiene un elemento. Ejemplo 7.11: Los conjuntos A={x/x es un pontfice entre los aos 1985 y 2005}={Juan Pablo II} y B={x?N / x2?4=0}={2} son unitarios.
7.7.5 Conjunto binario
El conjunto binario es aquel que est formado por dos elementos.
![]()
7.7.6 Conjunto universal

Ejemplo 7.13: dados los conjuntos U={1,3,5,7,9,11}, A={3,9,11}, B={2,5,7,9}, C={1,6} y D={1,7,11,5}, determine si U es conjunto universal respecto a los dems conjuntos. En efecto, U es un conjunto universal respecto a los conjuntos A y D, pero no con respecto a los conjuntos B y C. Por qu?
7.7.7 Conjunto infinito
Es aquel conjunto cuya cantidad de elemento no se puede contar; es decir, es aquel conjunto en que sus elementos no se pueden nombrar o enumerar. Son
![]()
![]()
7.8 Operaciones entre conjuntos
Las operaciones que pueden realizar con conjuntos son: la interseccin, la unin, la diferencia, la diferencia simtrica y el complemento.
7.8.1 Interseccin de conjuntos
La interseccin de dos conjuntos A y B es el conjunto formado por todos los elementos comunes de ambos conjuntos (sin repetir elementos), es decir, es el conjunto formado por todos los elementos repetidos y se denota
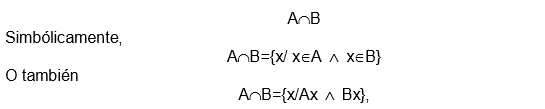
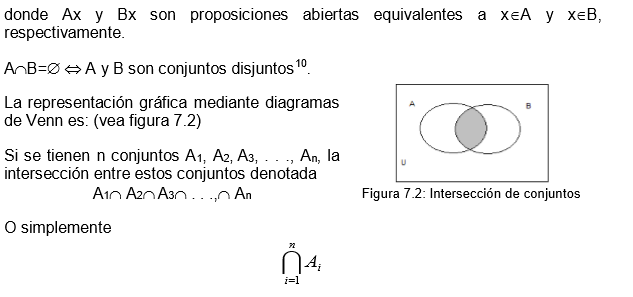
Se define como el conjunto formado por los elementos comunes de todos los conjuntos. Simblicamente,

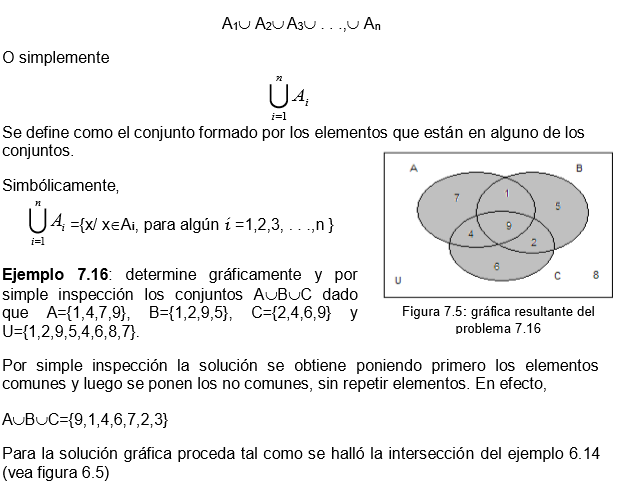
7.8.2 Unin de conjuntos
La unin de dos conjuntos A y B es el conjunto formado por todos los elementos comunes y no comunes de ambos conjuntos (sin repetir elementos) y se denota
Si se tienen n conjuntos A1, A2, A3, . . ., An, la unin entre estos conjuntos denotada
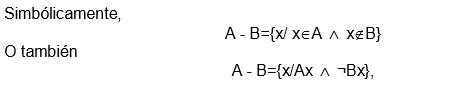
7.8.3 Diferencia de conjuntos
La diferencia entre de dos conjuntos A y B es el conjunto formado por todos los elementos no comunes del conjunto B respecto al conjunto A; es decir, los elementos que estn en A, pero no estn en B y se denota A-B
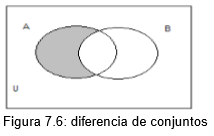
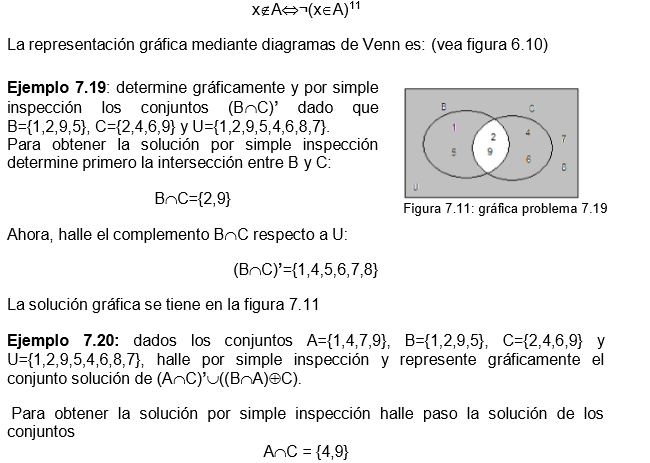
donde Ax y Bx son proposiciones abiertas equivalentes a x E A y x E B, respectivamente. La representacin grfica mediante diagramas de Venn es: (vea figura 7.6)
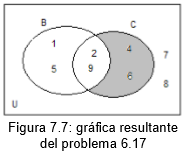

Ejemplo 7.17: determine grficamente y por simple inspeccin los conjuntos C-B dado que B={1,2,9,5}, C={2,4,6,9} y U={1,2,9,5,4,6,8,7}. Por simple inspeccin C-B={4,6} y grficamente vea figura 7.7.
7.8.4 Diferencia simtrica de conjuntos
La diferencia simtrica entre de dos conjuntos A y B es el conjunto formado por todos los elementos no comunes de ambos conjuntos; es decir, los elementos que no estn repetidos entre los conjuntos y se denota
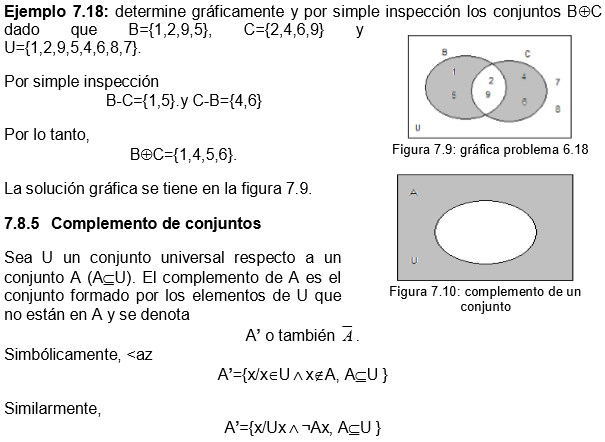
donde Ax y Bx son proposiciones abiertas equivalentes a x E A y x E B, respectivamente; su representacin grfica mediante diagramas de Venn se ve en la figura 7.8
donde Ax y Bx son proposiciones abiertas equivalentes a x E A y x E B, respectivamente. Observe que,
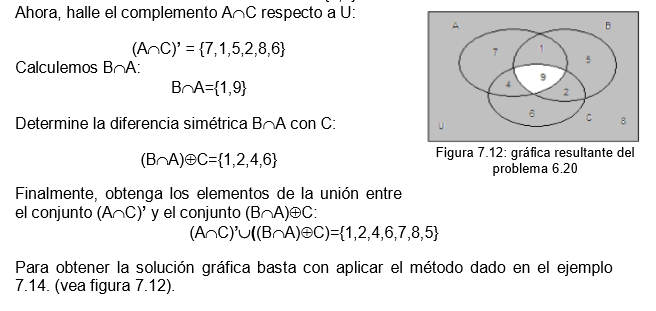
7.9 lgebra de conjuntos
El lgebra de conjuntos tal como la de proposiciones es un sistema axiomtico consistente, completo e independiente; se utiliza bsicamente para demostrar la igualdad entre conjuntos o construir y simplificar conjuntos complejos y siempre que tengan determinadas propiedades.
Signos lgicos. Corresponde a los conectivos que se trataron en el captulo de lgica proposicional y cuantificacional, son ellos:
![]()
Signos especficos. Estos signos tambin se reconocen como signos de relacin en la teora de conjuntos y se utilizan tres:
![]()
Letras. Se usan letras maysculas y minsculas con o sin ndices y subndices.
Signos de agrupacin. Se usan parntesis ?(? y ?)?, adems, las llaves ?{? y ?}?.
![]()
7.9.1 Postulados del lgebra de conjuntos
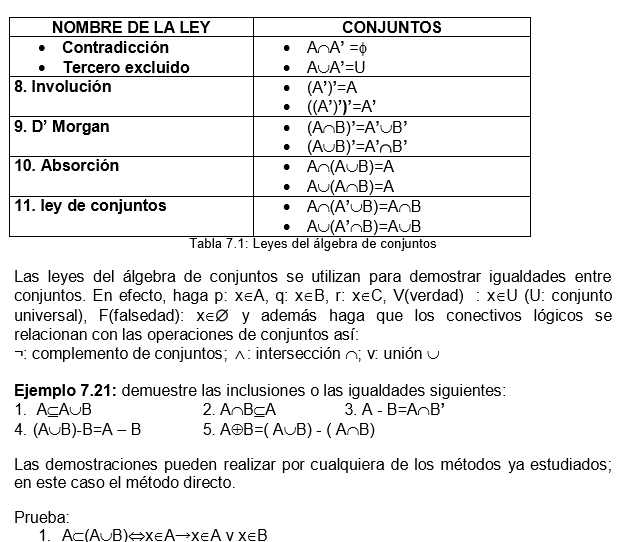
7.9.2 Leyes del lgebra de conjuntos



7.10 Conjunto potencia
El nombre de conjunto potencia proviene del hecho de que si un conjunto A tiene n elementos, la cantidad de subconjuntos que se pueden formar con los elementos de A es 2n. Este conjunto tambin se conoce como conjunto de partes de un conjunto
7.10.1 Concepto de conjunto potencia
Sean A y X conjuntos cualesquiera; el conjunto formado por todos los subconjuntos de A de denomina conjunto potencia y se denota por P(A). Simblicamente
![]()
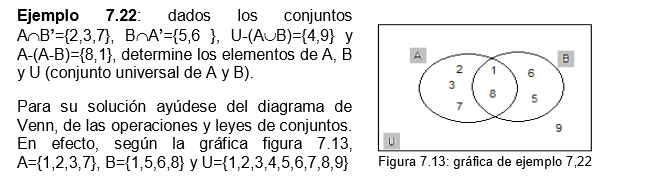
Ejemplo 7.23: Sean A y B conjuntos definidos como A={2}, B={1,2,3} y C=={ }.

7.10.2 Propiedades del conjunto potencia
Sean A, B, X conjuntos cualesquiera, entonces se tiene:
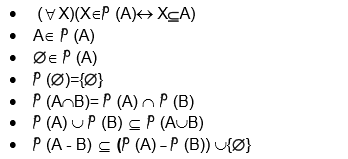
Ejemplo 7.24: Demuestre que

7.11 Nmero de elementos de un conjunto
Sea A un conjunto finito; el nmero de elementos de un conjunto denotado n(A) corresponde a un nmero natural que indica la cantidad de elementos del conjunto dado. El clculo del nmero de elementos de un conjunto consiste en contar los elementos del conjunto; por lo tanto, se considerarn conjuntos finitos. Se denominar n(A) al nmero cardinal de elementos de A o clase de A. As que los conjuntos que tengan igual nmero de elementos se podr llamar conjuntos coordinables o equipotentes, porque se puede establecer una biyeccin entre sus elementos. Si se dan conjuntos finitos y se determina el nmero de elementos de esos conjuntos, tambin se podr hallar de otros conjuntos tales como: la unin la interseccin, la diferencia y el complemento de dichos conjuntos.
![]()
Ejemplo 7.26: dados los conjuntos A={b, f, d} y B={2,6,8}, determine la clase a la cul pertenecen dichos conjuntos. Los conjunto A y B pertenecen a la clase 3, porque tienen la misma cantidad de elementos: n(A)=3, n(B)=3 y en efecto, son equipotentes o coordinables (forman relacin biunvoca).
7.11.1 Nmero de elementos de la unin de dos conjuntos

Ejemplo 7.27: dados los conjuntos A={2,3,5,7} y B={2,4,6,8} y C={1,9}, halle
![]()

7.11.2 Nmero de elementos de la unin de tres conjuntos

Su demostracin es bastante extensa sin embargo puede analizarla la igualdad de manera intuitiva con la ayuda de diagramas de Venn. Se podra creer que la igualdad debiese ser
![]()
pero esta identidad tiene sus contraejemplos. Presente algunos casos.
Ejemplo 7.28: una encuesta realizada a excursionistas de la ciudad de Medelln entre los ltimos 4 aos acerca de los que haban visitado a Argentina, Bolivia y Canad arroj la siguiente informacin:
48% haba ido a Argentina
46% haba ido a Bolivia
30% haba ido a Canad
26% haba ido a Argentina y Bolivia
15% haba ido a Bolivia y Canad
13% haba ido a Argentina y Canad
10% haba ido a los tres pases Se quiere saber: a) El porcentaje que no ha ido a ninguno de los tres pases
b) El porcentaje que ha ido a los sumo a dos pases
c) El porcentaje que ha ido al menos a dos de estos pases
d) El porcentaje que ha ido exactamente a un pas
e) El porcentaje que ha ido a Argentina y no a Canad
f) El porcentaje que ha ido a Bolivia o a Canad, pero no a Argentina
Para hallar solucin al problema se toma como recurso el diagrama de Venn para graficar el problema; luego, utilizando las leyes del lgebra proposicional (en algunos casos) y las operaciones de conjuntos lograremos la solucin. En efecto, veamos la grfica del problema: Designemos A: Argentina, B: Bolivia y C: Canad y U: 100% de los encuestados (figura 7.14) Para graficar tenga en cuenta, que se inicia primeramente con las instrucciones que indican interseccin (de pares de conjuntos y de los tres); que se completan los conjuntos dados y que el total, por ningn motivo, debe ser mayor que 100. Solucin de a: segn la grfica, el porcentaje que no ha ido a ninguno de los tres pases es 20%. Observe que est ubicado por fuera de los tres conjuntos.
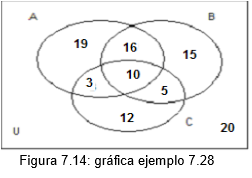
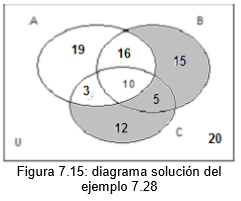
Solucin de b: La palabra ?a lo sumo? significa ?mximo?; en nuestro problema, donde se pide hallar los que mximo han ido a dos pases, es similar a que estn pidiendo los que han ido a 1 a 2 pases: 3%+15%+5%+16%+19%+12%=70% Solucin de c: La palabra ?al menos? significa ?mnimo?; en nuestro problema, donde se pide hallar los que mnimo han ido a dos pas, es similar a que estn solicitando los que han ido a 2 3 pases: 10%+16%+3%+5%=34% Solucin de d: Los que han ido exactamente a uno de estos pases son aquellos que viajado nicamente a Argentina o nicamente a Bolivia o nicamente a Canad. En efecto son: 15%+19%+12%=46% Solucin de e: el porcentaje que ha ido a Argentina y no a Canad corresponde a la seccin que est en A, pero no est en C. Por consiguiente, es: 19%+16%=35% Solucin de f: trascrito el problema al lenguaje simblico la expresin queda:
![]()
Trascribiendo la expresin de este enunciado a la teora de conjuntos se tiene:
![]()
La solucin se puede ver en el diagrama de la figura 7.15 se tiene: 15%+5%+12%=32% Otra forma de resolver este problema es: se utilizan los correspondientes valores de verdad de los conectivos lgicos de la expresin dada en lenguaje simblico, as: seleccione el conectivo principal de cada parntesis y el de la expresin escrita y ponga verdadero a esos conectivos. Por lo tanto, para que cada parntesis sea verdadero, escriba la tabla de valores de verdad de cada proposicin segn el conectivo lgico; entonces, las proposiciones verdaderas las deja como estn y las de valores falso, las niega. En efecto, (Bx v Cx)^Ax V V Como la proposicin Bx v Cx es compuesta, determine cules son los posibles que toma Bx y Cx para que su disyuncin sea verdadera.

AUTOEVALUCION 7








16) Resuelva el problema del ejemplo 7.28 las siguientes situaciones
a) El porcentaje que si ha ido a Canad o a Argentina, entonces no ha ido a Bolivia.
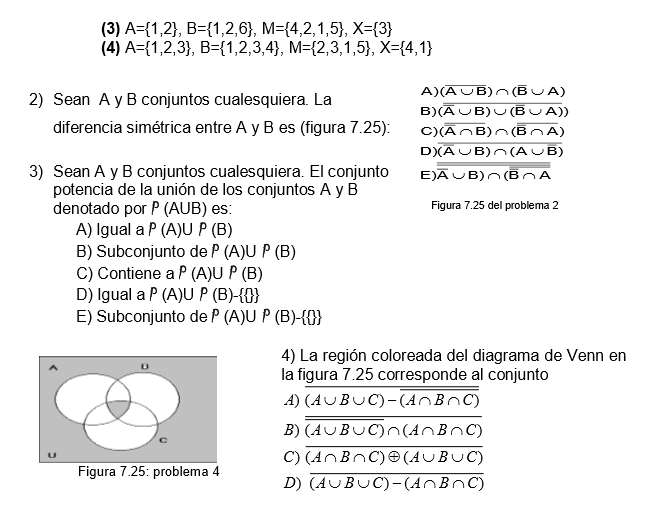
b) El porcentaje que ha ido a Argentina y no a do a Canad si, y slo no ido a Bolivia. 17) La revista de la universidad desea incrementar su tiraje y encarga a los estudiantes de comunicacin realizar una encuesta entre sus lectores. Esta, tras el correspondiente sondeo, procesa los datos y entrega a la revista las siguientes condiciones sobre sus lectores actuales: 53% son varones, 48% son estudiantes universitarios, 37% viven en Medelln, 8 % son universitarios varones, 16% son varones que viven en Medelln, 10% son universitarios que viven en Medelln, 5% son universitarios varones que viven en Medelln. El director de la revista, tras examinar los datos, concluye que no son ciertos y se niega a aceptarla. El tiene razn?. Por qu? 18) Se da la siguiente informacin referente al nmero de elementos de los subconjuntos A, B, C de cierto conjunto universal U. Determine el nmero de elementos de los conjuntos:
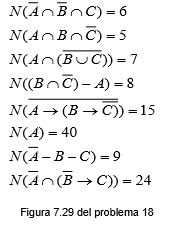
a) n(a lo sumo estn en dos conjuntos)
b) n(mnimo estn en dos conjuntos)
c) n(U) 19) En la facultad de administracin de una universidad 145 estudiantes del primer nivel toman matemtica moderna, 136 administracin, 138 economa, 94 toman matemtica y administracin, 78 economa y matemtica, 85 administracin y economa, 49 las tres materias y 54 ninguna de las tres materias.
a) Cuntos estudiantes hay en el primer nivel?
b) Cuntos estudian exactamente dos materias?
c) Cuntos estudian al menos una materia?
d) Cuntos estudian mximo una materia?
e) Cuntos estudian administracin, pero no matemtica?
f) Cuntos estudian economa si y solo si no estudian administracin? 20) En una universidad 145 estudiantes presentaron el primer parcial de matemtica moderna, en el que 52 perdieron dicho examen. Luego del segundo parcial el resultado fue muy favorable a los estudiantes, habindolo ganado 104. Si 34 estudiantes perdieron ambos exmenes Cuntos alumnos aprobaron dichos exmenes? R/. 86 21) En un grupo de 200 atletas hay 148 que tienen sudadera con chaqueta y 66 que tienen pantaloneta con camiseta. Cuntos hay que tienen pantaloneta y camiseta y pantaloneta con camiseta, sabiendo que 28 ni pantaloneta con camiseta ni sudadera con chaqueta? Cuntos tienen nicamente sudadera con chaqueta? Cuntos tienen nicamente pantaloneta con camiseta? R/.14;134; 52 22) En una encuesta hecha a 120 deportistas acerca de los que practicaban ftbol, voleibol y baloncesto, se encontr: nicamente ftbol 14; voleibol, pero no baloncesto ni ftbol 9; nicamente baloncesto 17; ftbol y voleibol, pero no baloncesto 15; ftbol y baloncesto, pero no voleibol 3; voleibol y baloncesto, pero no ftbol 6; ninguno de estos deportes 42.
a) Cuntos practican los 3 deportes?
b) Cuntos si practican ftbol y baloncesto entonces no practican voleibol?
c) Cuantos practican voleibol si y solo si no practican ftbol pero si baloncesto?
d) Cuantos practican al menos 2 deportes? e) Cuntos practican a lo sumo 1 deporte? 23) Haga un programa en cualquier lenguaje, que calcule las operaciones de conjuntos (unin, interseccin, diferencia, diferencia simtrica de conjuntos cualesquiera y complemento de un conjunto dado) y muestre grficamente los conjuntos.

