 Photo by Clark Young on Unsplash
Photo by Clark Young on Unsplash
One of the most frequently asked questions during the interviews is about time complexity. Even if you are a good problem solver, you have to take care of the time-complexity or as scientists name, Big-O Notation. Recently, I got a deep dive into that topic to prepare for the upcoming technical interview as a software engineer. I realized that plenty of articles here on Medium are talking about the same subject. However, In this article, I will try to conclude what I learned so far beside giving smart tips that make answering the time complexity question becomes easy. So, let?s start.
What is the time-complexity?
The simple definition is that it describes the performance of an algorithm. In other meaning, how much power/time the computer processor should do to run the algorithm. Let?s demonstrate by example to get a better sense of the time complexity.
Types of time-complexity
There are many types for run-time complexity. Once you understand them, it will be easy for you to recognize the runtime as a second nature.
The simplest one is the constant type O(1) which is the fastest run-time.
O(1) is the fastest run-time. Your algorithm should tend to that type.
Linear run-time example
Let?s try to understand harder type which is the linear complexity. The other types built on that one.
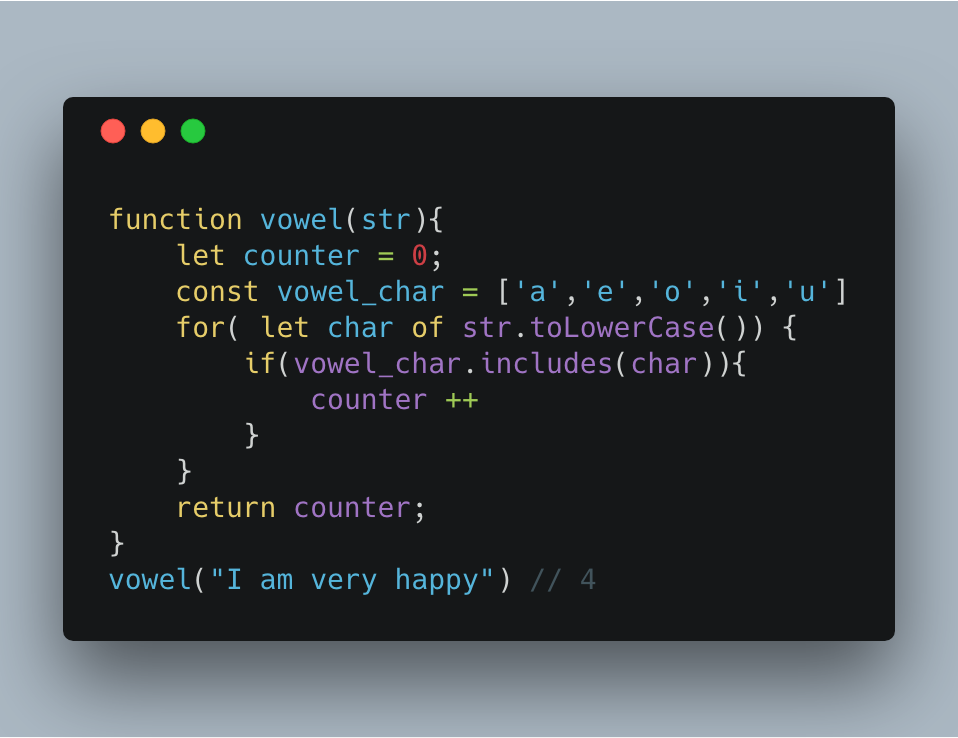
In the following example, we need to write a function that checks if the input string has a vowel. If the input string has a vowel, then return how many vowels.
Big-o Notation is the scientific term for time-complexity. Scientists and researchers used the name ?Big-O Notation? in the research and academic publications.
Building the algorithm
So, we can solve that problem by declaring a variable for counter and assign it to ?0?. Second, declare a constant variable for the vowel letters and set it equals to an array of vowels letters. After that, iterating over each character of the input string, Then, checking if that character included in the vowel array that we defined earlier. Finally, return the counter.
P.S: I set the vowels to an array because in case you want to add more letters in the future.
Discussing the solution in terms of time-complexity
After solving the problem, the interviewer will ask you what the run-time complexity for your solution. Or, how much processor power the computer should spend to run your algorithm? If your input becomes ?I am very happy today? you will have to repeat the for-loop by 5-times ? the number of letters in today. Means the processor have to increase the calculation power by N times in case we have N characters. This relation is a linear type.
When increasing the input size, time increased proportionally ? notice the green line.
The same if you are iterating through half of a collection, like when checking if the input string is a palindrome. The run-times n/2 which leads to being O(n).
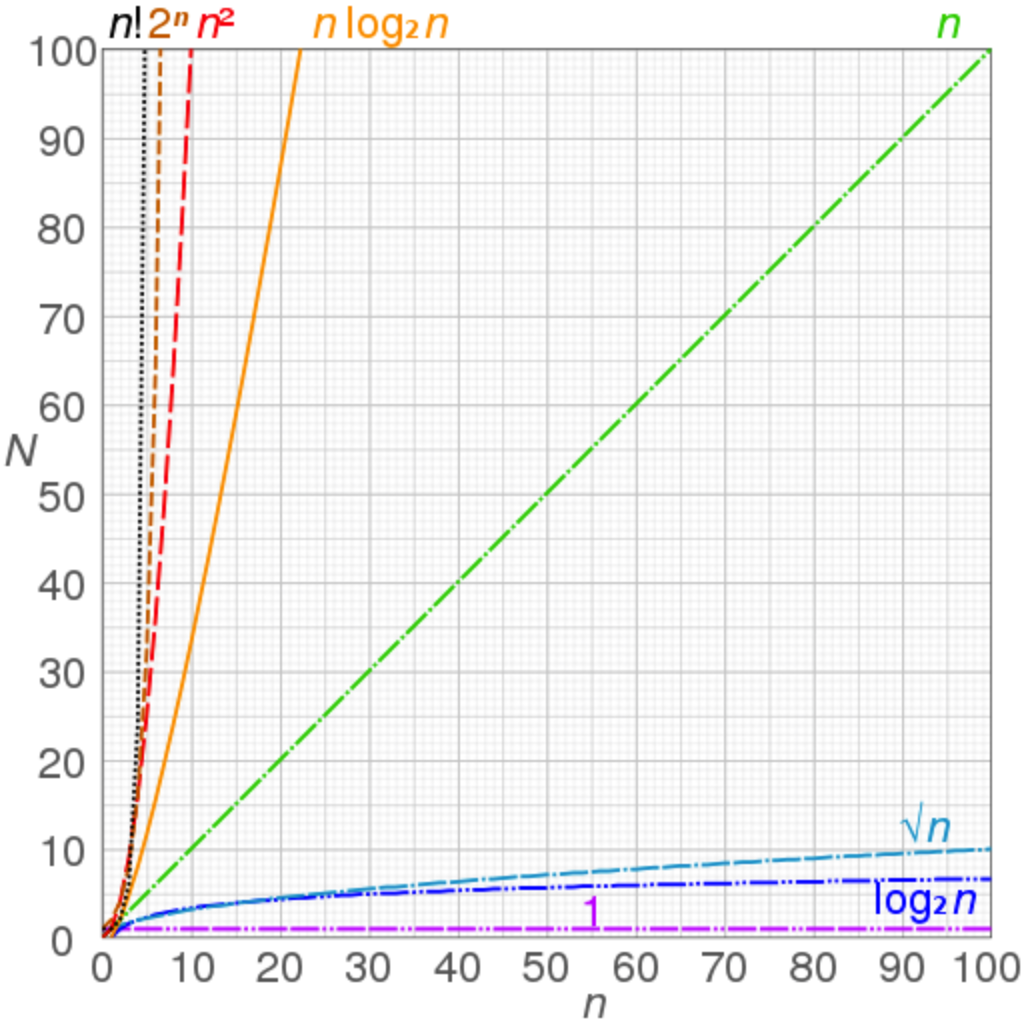 Graphs of functions commonly used in the analysis of algorithms, showing the number of operations N versus input size n for each function ? en.wikipedia.org/wiki/Big_O_notation
Graphs of functions commonly used in the analysis of algorithms, showing the number of operations N versus input size n for each function ? en.wikipedia.org/wiki/Big_O_notation
Quadratic runtime complexity
Quadratic means to double in mathematics. This equation called quadratic equation x + 4x + 4 = 0 this equation can be abstracted to (x + 2) = 0. So, in our case, if you have two nested loops iterating over the same collection, this will be a quadratic runtime complexity because you have loop. The processor need to double the work to run the algorithm.
So why is sorting is costing time?
I always asked my self that question until I got understand the logic behind that algorithm. The sorting algorithm takes O(n*log n) ? Quasilinear time, which is the best worst-case runtime we can get for sorting. To sort an array, usually, merge-sorting algorithm is being followed. Merge-sorting is to divide an array into two portions, sort them, then rejoin the two parts into one whole sorted collection. The following illustration demonstrates what precisely what is happening behind the scene.
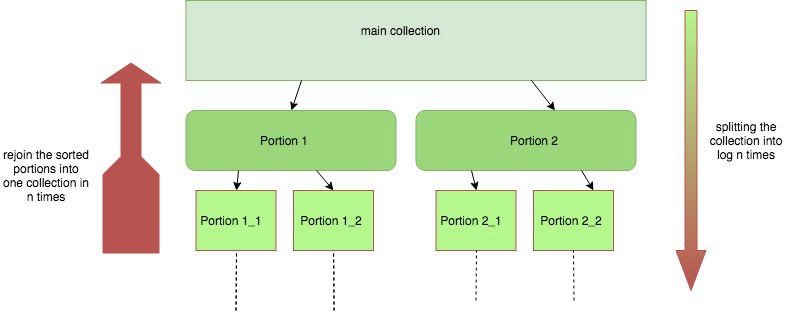 merge-sorting algorithm O(n*log n) ? quasilinear time
merge-sorting algorithm O(n*log n) ? quasilinear time
This algorithm takes O(n* log n) time, where log n, comes from the number of times we have to cut the collection n times in half to get down to the small arrays until we got just one element in the sub-array. However, The first (n) comes from the time cost of re-merging all (n) items in (n) time each time we join two sorted sub-collection ? the left side of the diagram.
Summarizing the run-time complexity types
I did a simple infographic that summarizes the different types of run-time complexity. The bars indicates the run time required for the processor to run the algorithm.
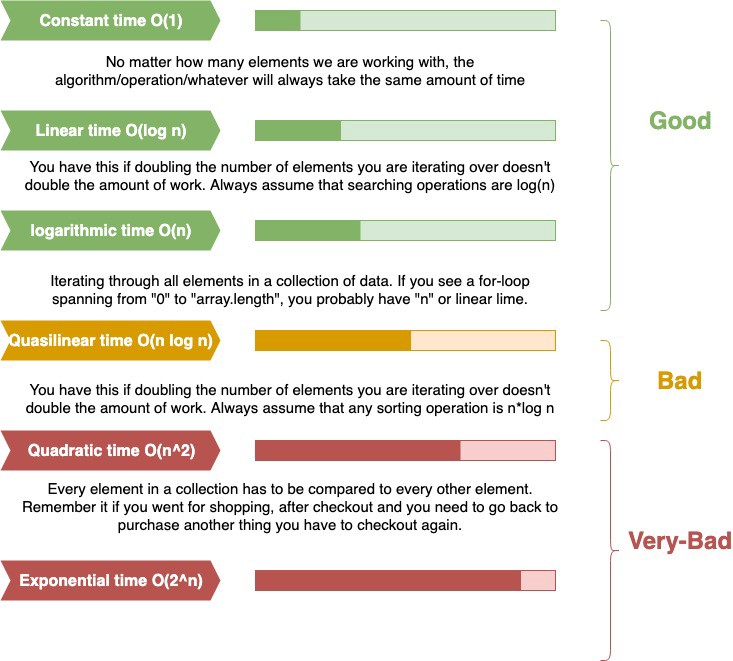 infographic illustrating the different types of run-time complexity.
infographic illustrating the different types of run-time complexity.
The cheat sheet guide
To recognize the runtime of each problem, I did a small cheat sheet to help you quickly figure out the run-time type and hence, you can improve your algorithm.
- If you are iterating over a single collection of elements using one loop, then run-time will be O(n).
- If you are iterating over half of the collection, it will be O(n/2) -> O(n).
- If you are iterating over two separate collections using two different loops, so it will become O(n+m) -> O(n).
- If you are iterating over a single collection using two nested loops, so it will be O(n).
- If you are iterating over two different collections using two nested loops, so it will become O(n*m) -> O(n).
- If you are sorting a collection, this becomes O(n*log(n)).
Conclusion
Time complexity is a vast topic to handle in just one article. In this post, I tried to give you a better starting point of where to start. I hope that I could describe the theory for you and make it clear to understand. In the reference section, you can find better resources to deep dive into that topic. If you liked my post, please give me a ? ? ? ? and follow me here on medium or leave a comment. You can follow me on twitter @salmaneg. Thanks for reading!!!
References:
- Interview cake ? logarithm in sorting.
- Wikipedia Big-O-Notation.
- Stability in sorting algorithm ? geeksforgeeks.
- Sorting algorithm visualization? toptal.
- If you like to deep dive, this collection of academic publication is enjoyable to read ? Kalle Rutanen


