ES6 arrays methods for set theory.
Hey! If you find my content useful, give me some ? on DEV.to/alvarosaburido or share a ?? with me:
Hi everyone, today I bring you some ES6 magic for common Array algorithms that sometimes, we overthink, and they have a really easy one-lined solution using high order functions like filter and Set theory.
What in the world is Set theory? Just a branch of mathematical logic that studies sets, which informally are collections of objects. We are not covering the same methods for Javascript Sets (Arrays and Sets are different data structures, you can take a look in this article to understand it better https://medium.com/front-end-hacking/es6-set-vs-array-what-and-when-efc055655e1a) but because Arrays are collections of homogeneous data, will be the same principle.
In this article, you will learn to implement these features.
Code
For all the examples, we have two arrays, A arrA=[1,3,4,5] & arrB=[1,2,5,6,7], we need a third array called C with the results of the operation. Let?s use some Venn Diagrams to help us visualize the concepts.
Intersection
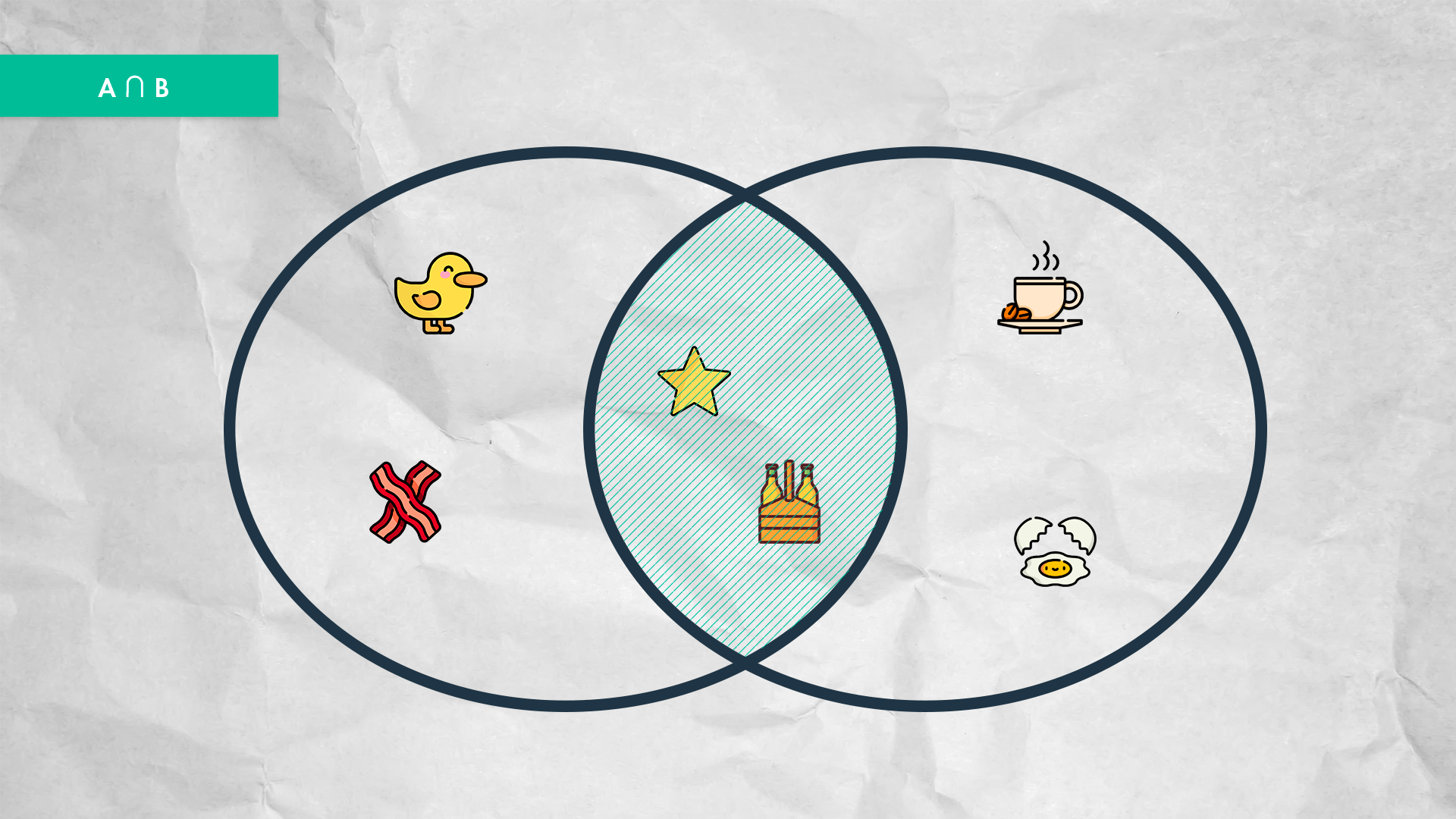Venn Diagram for the intersection of two sets.
The intersection will give us the elements that both arrays share in common, in this case, the result must be [1,5].
let intersection = arrA.filter(x => arrB.includes(x));
Difference
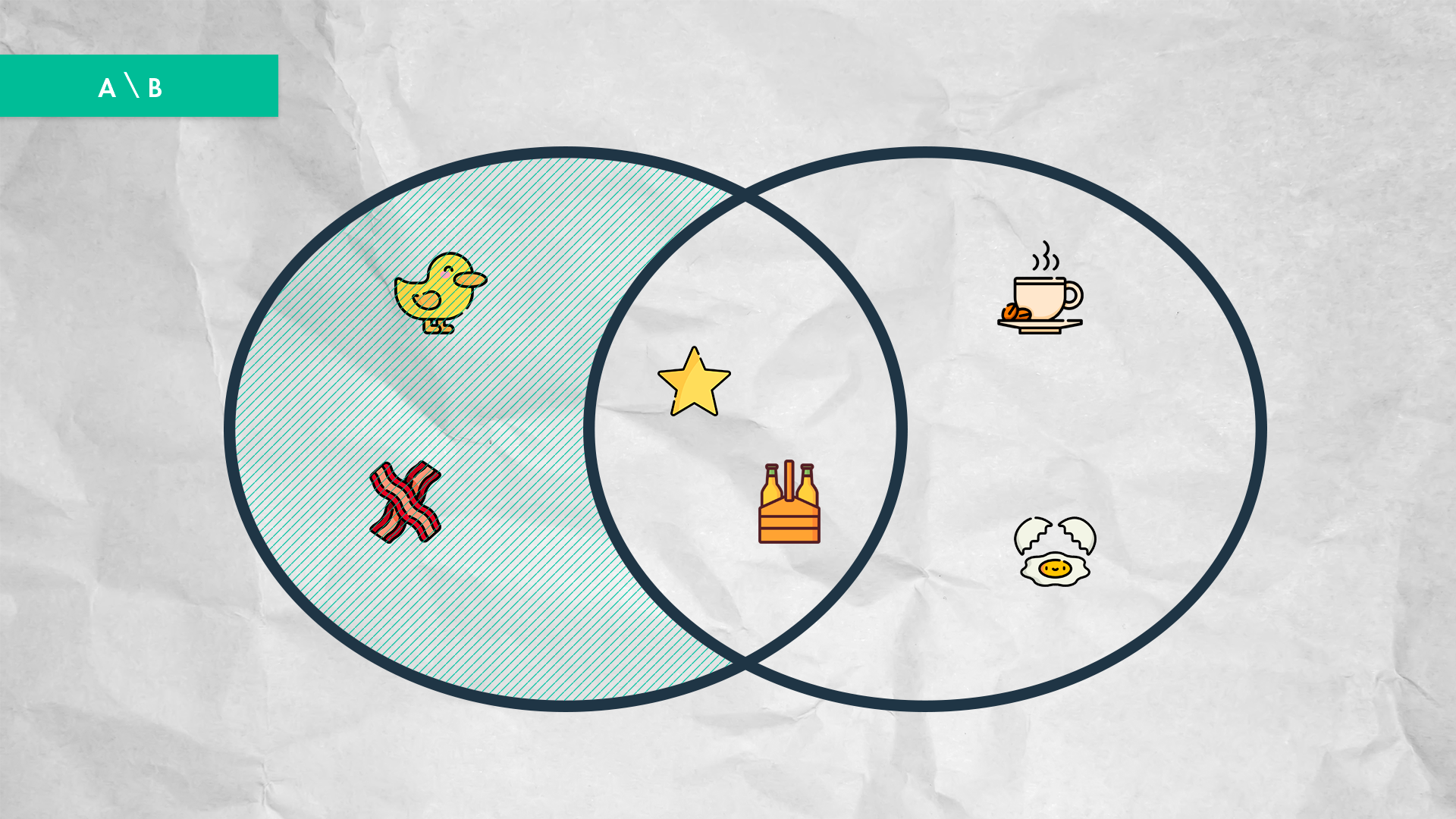Venn Diagram for the difference of two sets.
The difference will output the elements from array A that are not in the array B. The result will be [3,4].
let difference = arrA.filter(x => !arrB.includes(x));
Symmetrical Difference
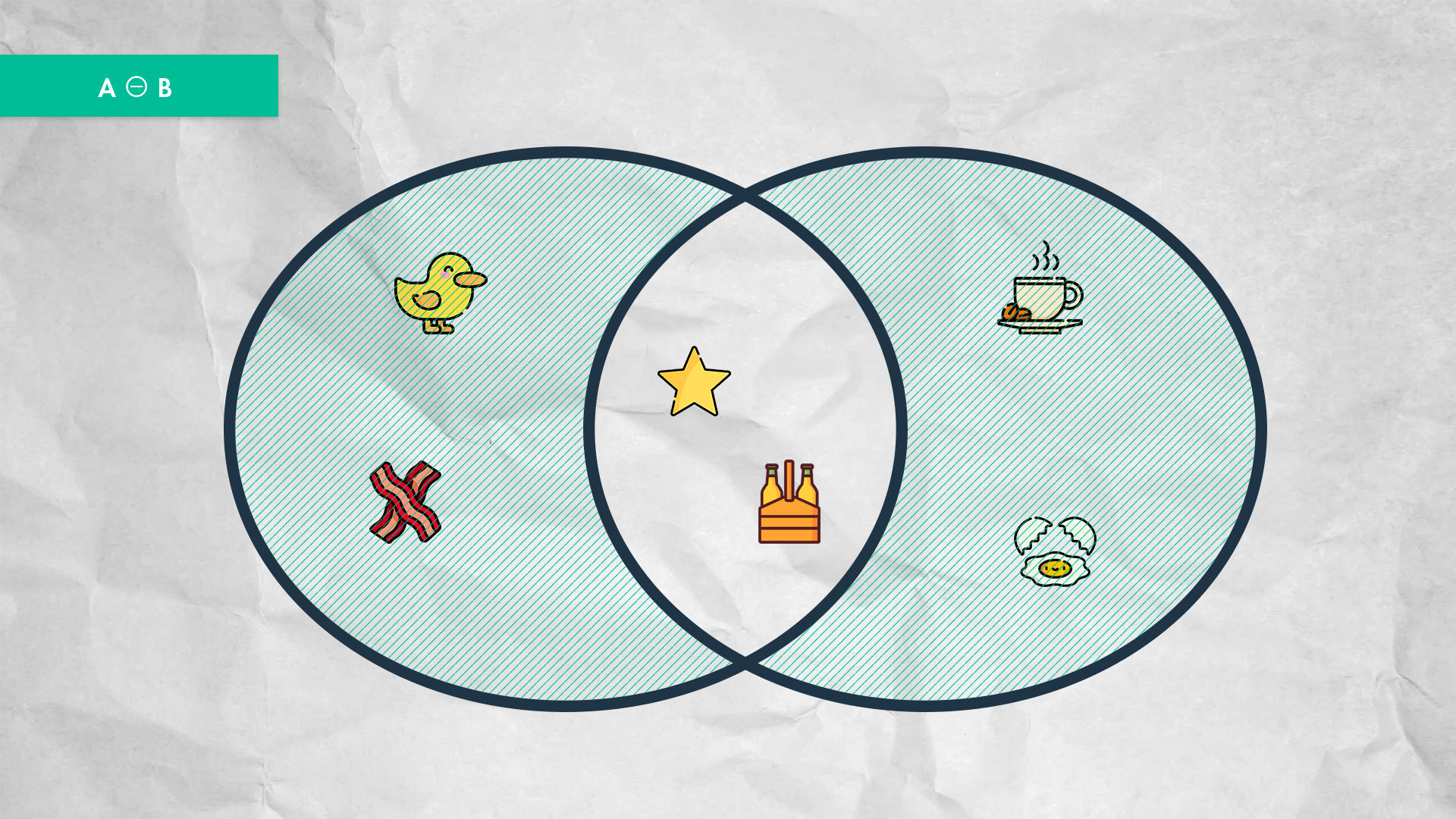Venn Diagram for the symmetrical difference of two sets.
In this case, you will get an array containing all the elements of arrA that are not in arrB and vice-versa, so the result should be [2,3,4,6,7].
let difference = arrA .filter(x => !arrB.includes(x)) .concat(arrB.filter(x => !arrA.includes(x)));
Union
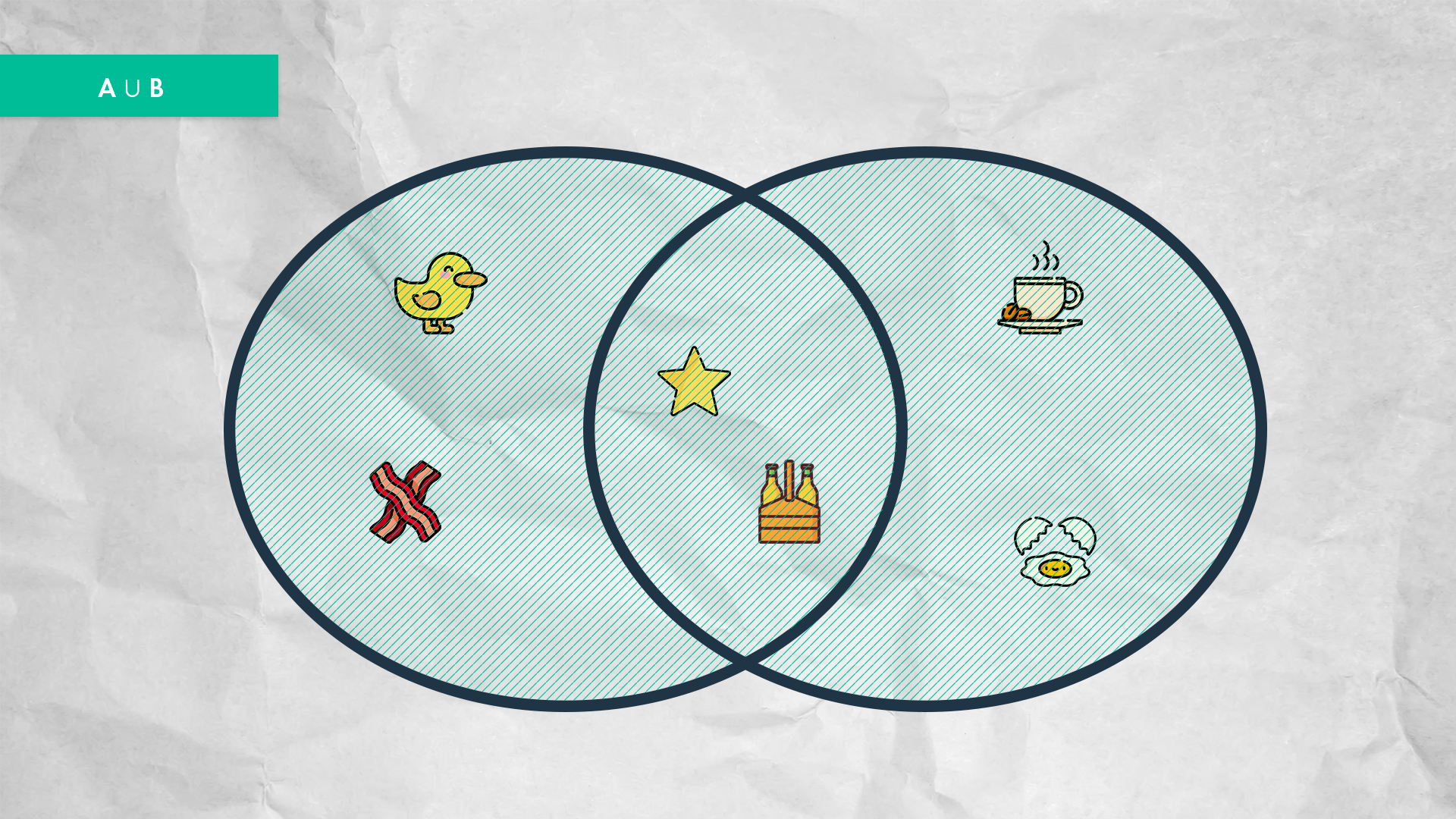Venn Diagram for the union of two sets.
The union must be the simplest of them all, in the end, the result should be all the elements from A, all from B, or both like this [1,2,3,4,5,6,7].
let union = […arrA, …arrB];
But, there is a problem is that if we use spread operator, we will get elements duplicated, so it?s no theoretically a union. For doing this we have can use a Set to help us out:
let union = […new Set([…arrA, …arrB)];
Why? In the article I mentioned earlier, Sets in javascript contains only distinct elements. So you will not have duplicates but will have to use Set Object.
So, right now, Plain vanilla ES6 can compete hand to hand with other implementations like jQuery, lodash or underscore, and you can reduce code from these:
function symmetricDifference(a1, a2) { var result = ; for (var i = 0; i < a1.length; i++) { if (a2.indexOf(a1[i]) === -1) { result.push(a1[i]); } } for (i = 0; i < a2.length; i++) { if (a1.indexOf(a2[i]) === -1) { result.push(a2[i]); } } return result;}
to one or two lines or code. Pretty useful Uh?
If you have a question, or another idea to resolve the Union problem, let me know in the comments, beer, and stars for all!.
I like to write a lot, but I no longer write on Medium, you can see a full list here blog.
