An in-depth study.
Photo: Imgur
Most contemporary physicists are concerned with technical, big-picture questions: Why do neutrinos have mass when the Standard Model says that they shouldn?t? Why are quantum field theory and general relativity irreconcilable even though both are empirically valid? Can nuclear fusion be used as an efficient power source? And so on. These questions are important but they aren?t really in line with the sort of everyday, practical problems that occupy the minds of the general public. For example, are cats liquids or solids?
The earliest (c. 2014) researcher to have seriously investigated this question seems to be a person named Tom who submitted his findings to the Funny Animals section of the journal Bored Panda in an article entitled ?15 Proofs That Cats are Liquids.? Drawing from the results of 15 experiments using a variety of cat breeds and container geometries, Tom concluded that cats have a tendency to assume the shape of their container, which is a fundamental property of both liquids and gases. Furthermore, cats in the experiment tended to show negligible change in volume, which is a characteristic property of liquids.
Perhaps unsatisfied by the strictly qualitative nature of Tom?s study and the peer review standards of Bored Panda, further research was conducted by Marc-Antoin Fardin at the cole normale suprieure (Paris) later in that same year using a more rigorous definition of ?liquid,? discussed in a letter entitled ?On the Rheology of Cats.? Fardin found that cats exhibit a much richer and more complex range of rheological behaviors than was found in the initial Bored Panda study and it is not strictly appropriate to say that cats are strictly liquids. For his work in advancing progress in cat physics and demonstrating the implications of that emerging field with regards to the broader study of continuum mechanics, and also for being really, really funny, Fardin was awarded the 2017 Ig Nobel Prize in Physics.
Liquids, solids, and gases
Enough joking around.
While Fardin?s paper was obviously intended to be humorous, it does at least play at taking the question seriously and discusses the question using the language of modern rheology, the branch of mechanics that studies the motion of materials that have both fluid and solid characteristics. Rheology is itself a branch of continuum mechanics, which studies the motion of macroscopic bodies of matter that are assumed to completely fill the space they occupy (i.e. ignoring molecular structure and other microscopic flaws and discontinuities).
The types of materials that are studied in continuum mechanics can be placed on a sliding scale based on how hard it is to change their shape. At one end, there are the ideal Newtonian fluids which offer no resistance at all to applied stresses and will continue to change their shape, or deform, for as long as those stresses are applied no matter how weak those stresses are. At the other end are the ideal rigid solids which will never deform under any stress no matter how strong.
Since flowing motion is built up from infinitesimal deformations, we could also say that a Newtonian fluid is a sample of matter that can only flow and cannot be pushed since it will just flow out of the way, and a rigid solid is a sample of matter that can only be pushed and cannot flow. Rheology studies the motion of matter that falls near the middle of this scale, which can be said to have both solid and liquid properties depending on circumstances.
For example, glaciers are made of solid ice and when observed for short periods of time they appear solid, but over long enough time scales a glacier will move and flow just like a river of liquid water.
Ordinary liquid water shows similar behavior. When a water balloon is punctured, the water doesn?t immediately splash out. For a tiny fraction of a second, the water roughly holds the shape of the balloon:
This suggests that over very short periods of time, water has solid-like behavior and only begins to act like a liquid when observed for a long enough time.
These are two examples of a general trend: a sample of matter will tend to act more like a liquid over long periods of time and more like a solid over short periods of time.
To characterize whether a sample of material acted more like a solid or liquid in a particular experiment, we assign that material a Deborah number:
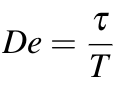
In this formula, T is the duration of the experiment and ?, called the relaxation time, is a characteristic time scale over which a given material tends to carry out deformation processes. How this is to be determined will depend on the experiment being conducted. A Deborah number greater than one means a material acts more like a solid in the experiment and a Deborah number less than one means a material acts more like a liquid.
In his paper, Fardin assumed that the experimental time was fully under control and therefore he investigated the relaxation time in order to determine the extent to which cats are liquid.
So are cats liquid?
Fardin conducted a very simple investigation to find a range of possible values of the relaxation time. Using cutting-edge numerical simulations courtesy of the website Cat Bounce, Fardin concluded that a cat acts like a solid for experimental time scales of T~1 second. We could also reach the same conclusion by noting that when a cat is dropped from a small height (fall time ~1 second), the cat will act like a rigid rotating body as it positions itself to land on its feet.
For longer time scales, Fardin considers the following example of a kitten settling in to a wine glass:
Photo: Huffington Post
In this example, the kitten has assumed the geometry of its container after settling into its equilibrium state, and therefore acted like a liquid. Observations of cats find that the time it takes for them to locate, enter, and settle into a container is no more than a few minutes, so it?s fair to say that cats act like liquids on time scales of T~1 minute.
Demonstration of a relatively short settling process. Image: Suhak Natasha/YouTube
Since cats act like solids on experimental time scales of order one second and liquids on experimental time scales of order one minute, the time ? for which the Deborah number is equal to one can be estimated to be between one second and one minute.
So the answer to the question is yes. Given at least 60 seconds, a relaxing cat will be a liquid in the sense that liquid-like dynamical behavior will dominate over solid-like behavior.
Fardin also notes as an aside that longhairs can also behave like gases since their fur can expand to fill a container:
Images: KNS News, Thinkadinky
We will now discuss some other rheological properties of cats that were investigated by Fardin.
Precise determination of the relaxation time
Fardin treats the relaxation time ? as a scalar quantity, meaning a pure number, in his experiments, but this need not be the case. In general, ? is a quantity called a second rank tensor, meaning it has a dependence on the choice of reference frame. In particular, ? can depend on the direction in which stress is applied to a sample relative to a special set of axes that are fixed in the sample called the principle axes. The principle axes can be used to efficiently describe the orientation of the sample and they can be thought as providing a coordinate system that is in some sense ?natural? given the sample?s geometry and distribution of density.
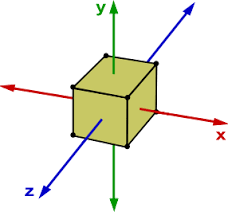The principle axes of a rigid and uniformly dense cube originate at the center and point through the faces. The response of this cube to a force applied at the surface will depend on the direction of the force and the coordinates of the point of application relative to the principle axes. Image: Chegg.
For bodies with more complicated geometry, especially deformable bodies, the determination of the principle axes is much more complex and we won?t address it here. However, if the body is much longer than it is wide or deep, it can make sense to speak of its long axis (a line through the center of mass in the direction of the body?s length) as the principle axis. A deformation along the principle axis is called an extension and a deformation perpendicular to this axis is called shearing.
In the absence of a container, cats seem to prefer to relax lengthwise, with their backs straight, as in this example.
Photo: Bertomic
Some cats will even deliberately seek out long containers, as in this example cited in Fardin?s paper:
Source: BlazePress
This suggests that cats have a shorter relaxation time for extensional deformation than for shear deformation, so cats will be ?more liquid? in containers that are significantly longer than they are wide. So the question of whether cats are liquid or solid depends not just on observation time but also on the geometry of the container.
Tribology: wetting and superfelidiphobicity
Tribology is the study of surfaces that are in contact and undergoing motion relative to each other. When one of the surfaces is solid and one is liquid, we may be interested in whether the liquid ?wets? the solid surface. A liquid is said to wet a particular surface when a droplet of liquid spreads freely on the surface. This occurs because intermolecular forces between the solid surface and the liquid are enough to overpower surface tension. On the other hand, when surface tension is stronger than the intermolecular forces, the liquid maintains a droplet shape and we say that the liquid does not wet the surface. For water, we say that water wets a hydrophilic surface and does not wet a hydrophobic surface. A surface that is extremely difficult to wet, such that droplets maintain a nearly spherical shape, is said to be superhydrophobic or ultrahydrophobic.
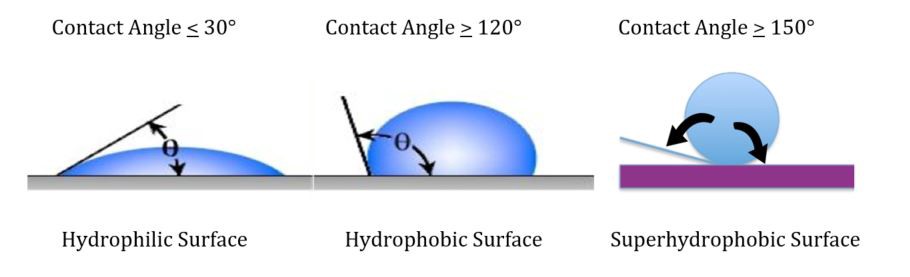Source: Prospector
A droplet of water on a lotus leaf. Lotus leaves are ultrahydrophobic. Source: Wikimedia Commons
Following this terminology, a surface is felidophilic if cats spread out freely over it and easily maintain contact and felidophobic if they do not.
Fardin provides the following example of a superfelidophobic surface, i.e. a straw basket. Note the very high contact angle.
Source: Cheezburger
There is not yet enough evidence to draw any conclusions about the causes of superfelidiphobicity, though a Cassie-Baxter model is likely appropriate. The Cassie-Baxter model says that microscopically rough surfaces, such as lotus leaves, are superhydrophobic because surface tension causes the droplets to rest on top of the bumps in the surface?s microscopic texture.
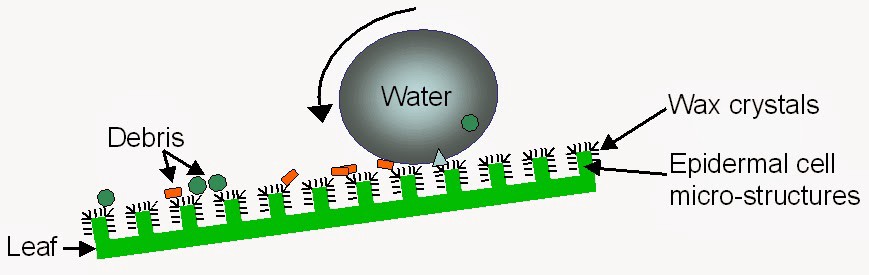Schematic of a water droplet on the surface of a lotus leaf. The lotus plant evolved to have superhydrophobic leaves so that water droplets would clean them. Source: Biomimicry Report
However, this ?lotus leaf effect? would be in reverse. Instead of a rough surface repelling the smooth water droplet, instead the rough cat?s fur is repelled by smooth surfaces, in this case the smooth surface of the basket. To further support this, Fardin notes that cats prefer to spread out on rough surfaces, such as the following extreme example:
Source: ItVirtove
And from practical experience, we know that cats seem to prefer rough surfaces like carpets, pillows, and keyboards to rest on. On the other hand, cats can have difficulty maintaining contact with very smooth surfaces, such as tile floors:
Source: Mr7Funny/YouTube
In particular, cats have an extremely low affinity for water surfaces:
Source: Eplaku
Flow instabilities
Flowing motion occurs when a body of material is being continuously deformed everywhere in its volume. When the rate of deformation becomes very large, more complicated fluid behaviors called secondary flows begin to emerge and eventually chaotic turbulent motion dominates the flow when the rate of deformation is great enough. In an experiment where the relaxation time is ?, the regime of the flow is given by the Reynolds-Weissenberg number:
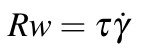
Where ??? is the magnitude of the rate of change of the deformation. For Rw<1, the flow is simple and steady. This is called the laminar base flow. For Rw~1, secondary flows start to become significant. As Rw continues to increase beyond 1, flow processes that cause the flowing motion to break down and change from a well-behaved motion to a chaotic motion will eventually begin to emerge. These processes are called instabilities.
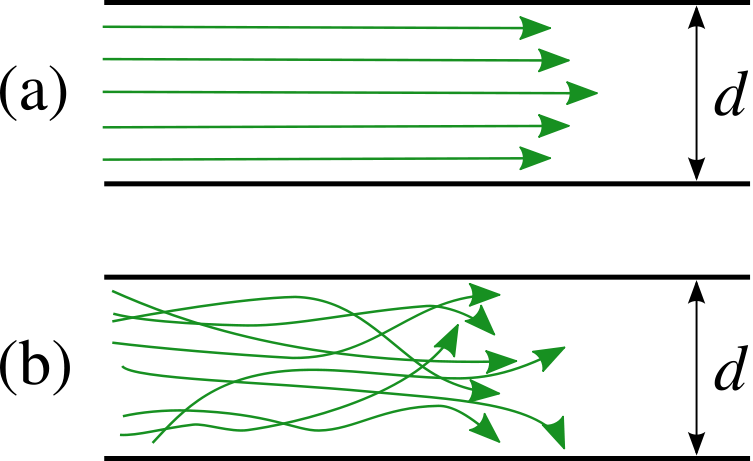Transition from stable flow (a) to turbulent flow (b). Source: Wikimedia Commons.
So, do cats demonstrate flow instabilities for increasing values of Rw?
Vortices are one of the simplest examples of turbulent flow. A vortex flow is when the fluid is revolving around an axis, such as in the following picture:
Vortex motion caused by a passing airplane wing. Red smoke was used to visualize the turbulent motion of the air as it was disturbed by the passing wingtip. Source: Wikimedia Commons.
Fardin cites the example of a cat rotating in a cylindrical container, to show that cats definitely exhibit rotational motion:
Source: Guremike
Furthermore, cats can undergo vortex motion even without the presence of a container:
Source: CFC
So turbulence is possible, but there is a major complication. Fardin explains that cats, unlike simple ?passive? fluids like water or air, are ?active?, meaning that they have their own motive power and can move spontaneously without external influence. Therefore cats may undergo turbulent motion even when subject to negligible stresses and thus very low values of ???. This means that we cannot yet conclusively determine whether increasing Rw must lead to flow instabilities.
What was the point of all of this?
Obviously this is a joke. Everything here and in Fardin?s paper is patently absurd. That said, except for a few instances of clever wordplay and terminology stretched to the breaking point, nothing that Fardin wrote is technically untrue.
The point is that pretending to take the ?cats are liquid? meme seriously allows for an entertaining and accessible introduction of many important ideas in continuum mechanics, one of the main parts of modern physics and the foundation of mechanical and civil engineering.
Your regularly scheduled math posting will now return.
