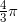Working 2,000 years before the development of calculus, the Greek mathematician Archimedes worked out a simple formula for the volume of a sphere:
![]()
Of his many mathematical contributions, Archimedes was most proud of this result, even going so far as to ask that the method he used to work out the formula???a diagram circumscribing a sphere inside a cylinder along with the ratio 2:3??be imprinted on his gravestone.
Archimedes? formula may have been a stroke of scientific genius in 250 B.C., but with the help of modern calculus the derivation is extremely simple. In this post I?ll explain one way to derive the famous formula, and explain how it can be done in dimensions other than the usual three.
The Derivation
Consider the diagram below. It?s a sphere with radius r. The goal is to find the volume, and here?s how we do that.
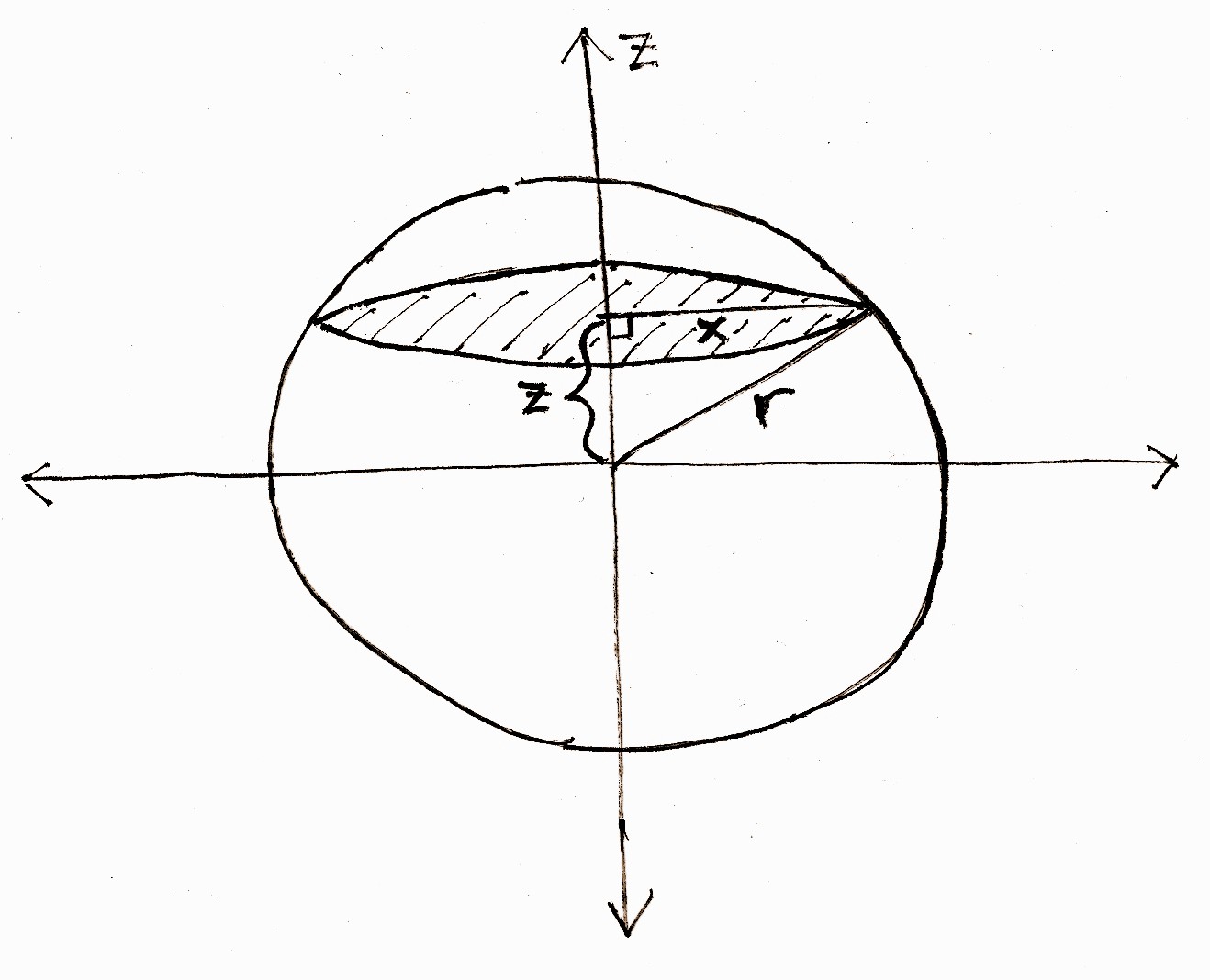
Notice that one thing we can easily find is the area of a single horizontal slice of the ball. This is the shaded disk at the top of the diagram, which is drawn at height z. The disk has a radius of x, which we?ll need to find the area of the disk. To find x, we can form a right triangle with sides z and x, and hypotenuse r. This is drawn in the figure. Then we can easily solve for x.
By the Pythagorean theorem, we know that
![]()
so solving for x we have
![]()
Then the area of the shaded disk is simply pi times the radius squared, or
![]()
Now that we have the area of one horizontal disk, we want to find the area of all horizontal disks inside the ball summed together. That will give us the volume of the sphere.
To do this, we simply take the definite integral of the disk area formula from above for all possible heights z, which are between -r (at the bottom of the ball) and r (at the top of the ball). That is, our volume is given by
![]()
![]()
![]()
![]()
Which is the volume formula we were looking for.
This same logic can be used to derive formulas for the volume of a ?ball? in 4, 5, and higher dimensions as well. Doing so, you can show that the volume of a unit ball in one dimension (a line) is just 2; the volume in two dimensions (a disk) is
![]()
and ? as we?ve just shown ? the volume in three dimensions (a sphere) is
![]()
Continuing on to four, five, and ultimately n dimensions, a surprising result appears.
It turns out the volume of a unit ball peaks at five dimensions, and then proceeds to shrink thereafter, ultimately approaching zero as the dimension n goes to infinity.