This blog post is a continuation of a series of blog posts about Algorithms, as it has been a hard concept for me to grasp as a programmer. Feel to check out the first blogpost about Algorithms, where I provide an introduction of what Algorithms are and an example of an algorithm and the second blog post about Data Structures, where I explained what are Data Structures and what are some types of Data Structures. Also check out the third blog post about Time Complexity and Space Complexity, which I provide an explanation of Time and Space Complexity. I have also written a blog post about Big O Notation. Recently I have written blog posts about Binary Search, Linear Search, Interpolation Search, Sorting Algorithms, Selection Sort, and Insertion Sort.
This blog post I will focus on Merge Sort. I will explain what Merge Sort is, how Merge Sort is associated with Algorithms, try to break down Merge Sort step by step and provide an example.
What is Merge Sort and how is it associated with Algorithms?
Merge Sort is a sorting algorithm, which is commonly used in computer science. Merge Sort is a divide and conquer algorithm. It works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. So Merge Sort first divides the array into equal halves and then combines them in a sorted manner.
Merge Sort Algorithms: Steps on how it works:
- If it is only one element in the list it is already sorted, return.
- Divide the list recursively into two halves until it can no more be divided.
- Merge the smaller lists into new list in sorted order.
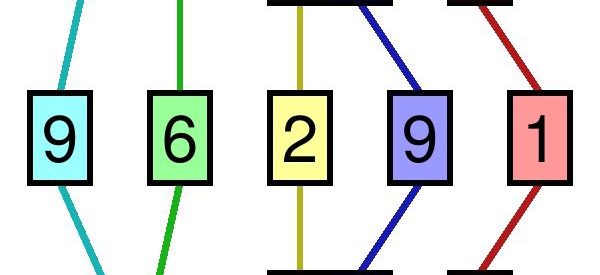
Below is an image of an array, which needs to be sorted. We will use Merge Sort Algorithm, to sort this array:
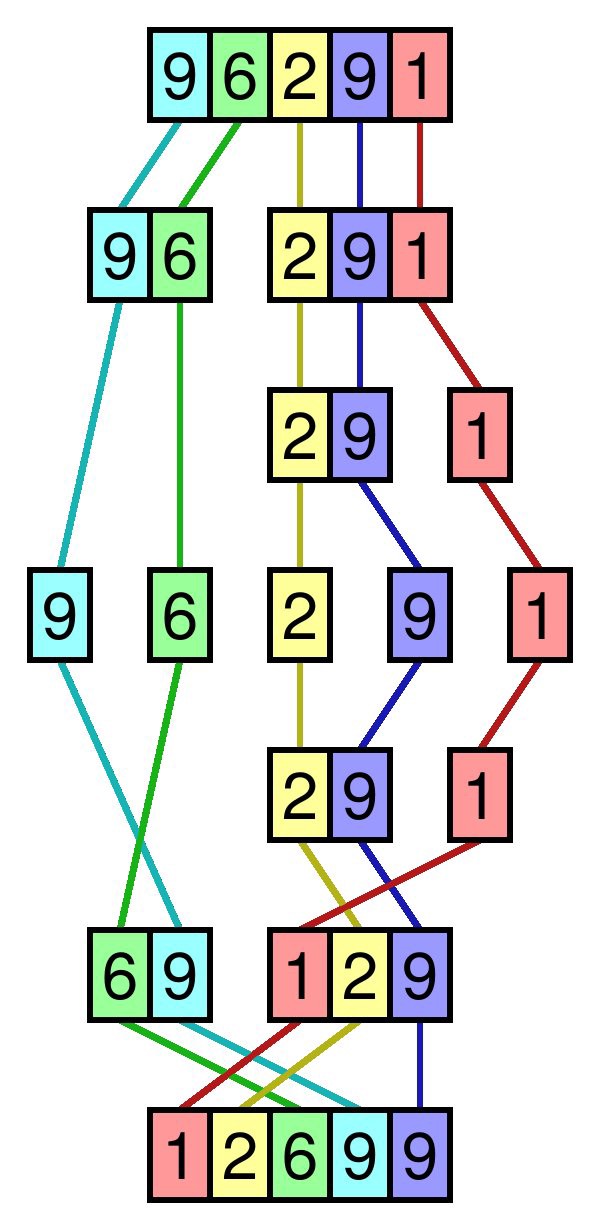
And here is another image and a YouTube video which provides an example of Merge Sort:
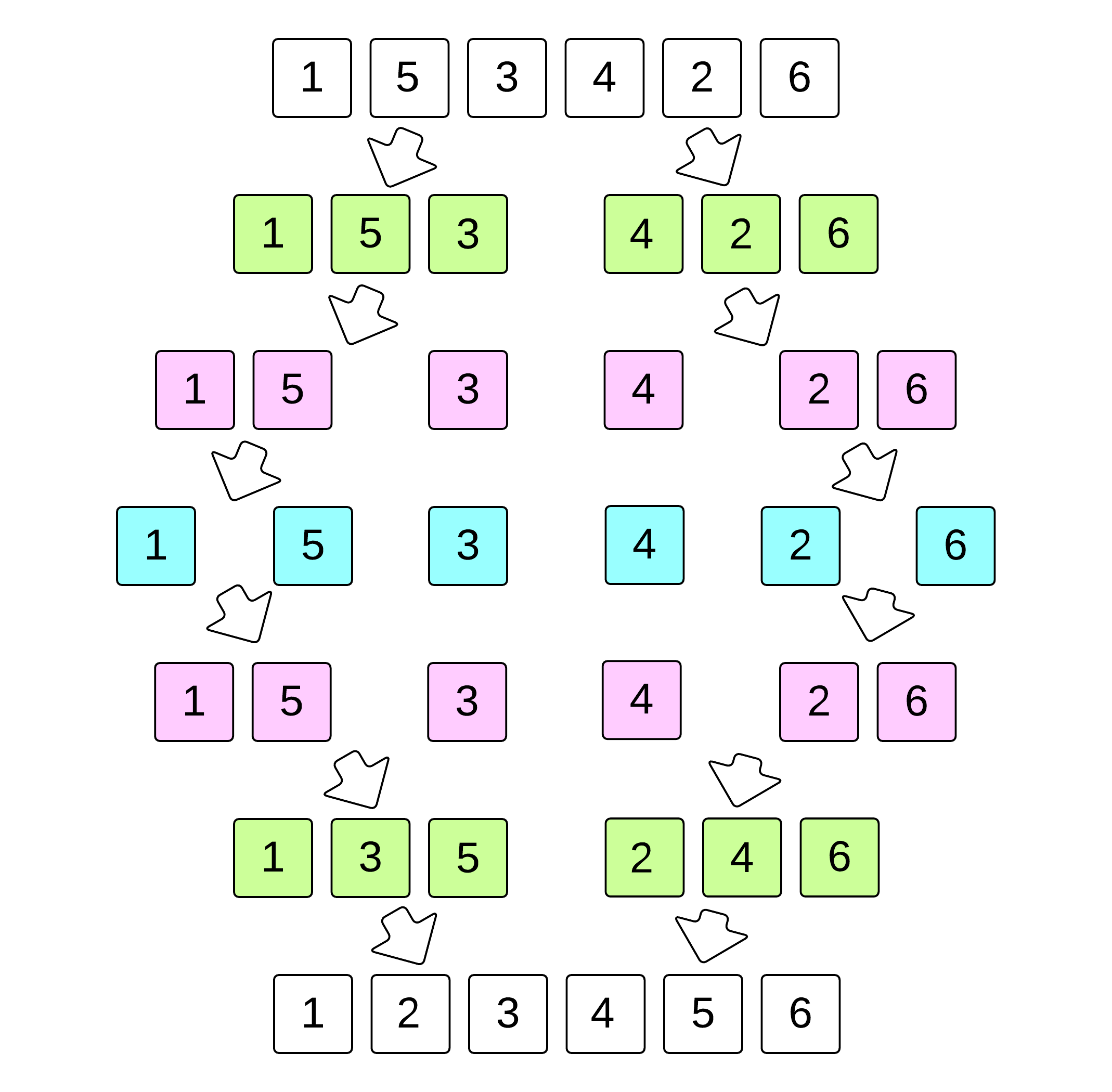
Merge Sort: An example
Here is an example of writing the Merge Sort Algorithm based on the steps I provided earlier. Below I have written a function, which accept the following parameter: an array. The function returns the sorted array.
Important Characteristics of Merge Sort:
- Merge Sort is useful for sorting linked lists.
- Merge Sort is a stable sort which means that the same element in an array maintain their original positions with respect to each other.
- Overall time complexity of Merge sort is O(nLogn). It is more efficient as it is in worst case also the runtime is O(nlogn)
- The space complexity of Merge sort is O(n). This means that this algorithm takes a lot of space and may slower down operations for the last data sets.
Overall Merge Sort is an important concept to understand when it comes to algorithms. Thank you for reading this blog post. In upcoming blog posts of this series, I will go over other sorting algorithms like quick sort.