Start using and understanding ReLU without BS or fancy equations
Originally appeared at https://www.tinymind.com/learn/terms/relu.

ReLU stands for rectified linear unit, and is a type of activation function. Mathematically, it is defined as y = max(0, x). Visually, it looks like the following:
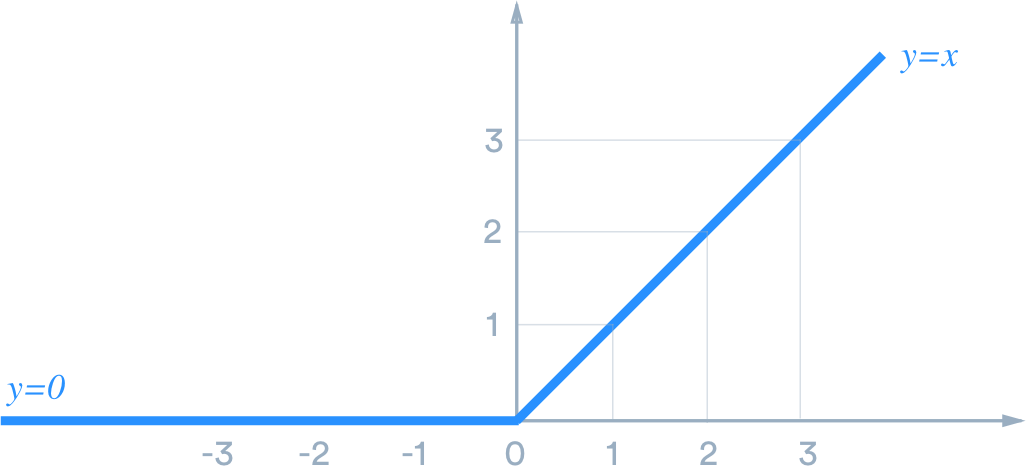
ReLU is the most commonly used activation function in neural networks, especially in CNNs. If you are unsure what activation function to use in your network, ReLU is usually a good first choice.
How does ReLU compare
ReLU is linear (identity) for all positive values, and zero for all negative values. This means that:
- It?s cheap to compute as there is no complicated math. The model can therefore take less time to train or run.
- It converges faster. Linearity means that the slope doesn?t plateau, or ?saturate,? when x gets large. It doesn?t have the vanishing gradient problem suffered by other activation functions like sigmoid or tanh.
- It?s sparsely activated. Since ReLU is zero for all negative inputs, it?s likely for any given unit to not activate at all. This is often desirable (see below).
Sparsity
Note: We are discussing model sparsity here. Data sparsity (missing information) is different and usually bad.
Why is sparsity good? It makes intuitive sense if we think about the biological neural network, which artificial ones try to imitate. While we have billions of neurons in our bodies, not all of them fire all the time for everything we do. Instead, they have different roles and are activated by different signals.
Sparsity results in concise models that often have better predictive power and less overfitting/noise. In a sparse network, it?s more likely that neurons are actually processing meaningful aspects of the problem. For example, in a model detecting cats in images, there may be a neuron that can identify ears, which obviously shouldn?t be activated if the image is about a building.
Finally, a sparse network is faster than a dense network, as there are fewer things to compute.
Dying ReLU
The downside for being zero for all negative values is a problem called ?dying ReLU.?
A ReLU neuron is ?dead? if it?s stuck in the negative side and always outputs 0. Because the slope of ReLU in the negative range is also 0, once a neuron gets negative, it?s unlikely for it to recover. Such neurons are not playing any role in discriminating the input and is essentially useless. Over the time you may end up with a large part of your network doing nothing.
You may be confused as of how this zero-slope section works in the first place. Remember that a single step (in SGD, for example) involves multiple data points. As long as not all of them are negative, we can still get a slope out of ReLU. The dying problem is likely to occur when learning rate is too high or there is a large negative bias.
Lower learning rates often mitigates the problem. If not, leaky ReLU and ELU are also good alternatives to try. They have a slight slope in the negative range, thereby preventing the issue.
Variants
Leaky ReLU & Parametric ReLU (PReLU)
Leaky ReLU has a small slope for negative values, instead of altogether zero. For example, leaky ReLU may have y = 0.01x when x < 0.
Parametric ReLU (PReLU) is a type of leaky ReLU that, instead of having a predetermined slope like 0.01, makes it a parameter for the neural network to figure out itself: y = ax when x < 0.
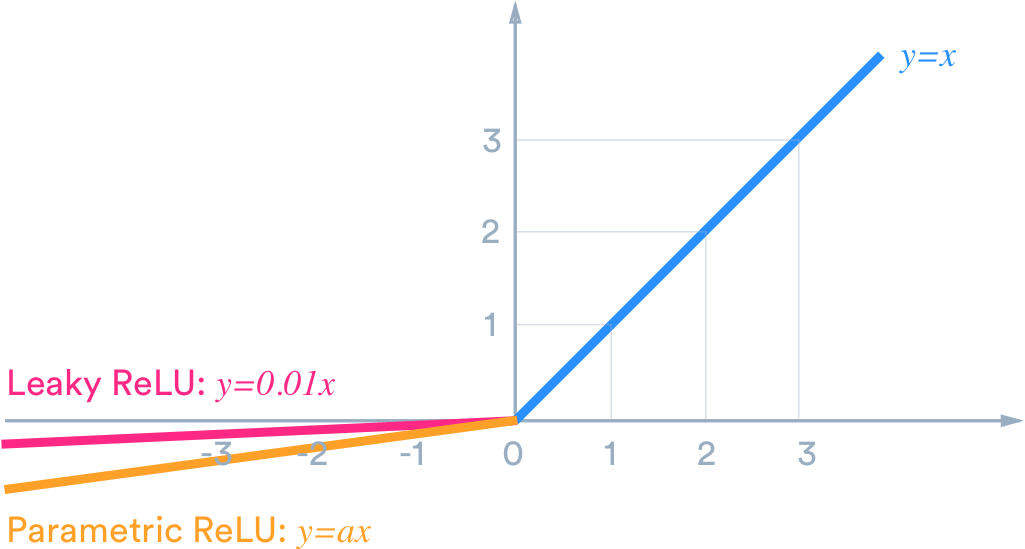
Leaky ReLU has two benefits:
- It fixes the ?dying ReLU? problem, as it doesn?t have zero-slope parts.
- It speeds up training. There is evidence that having the ?mean activation? be close to 0 makes training faster. (It helps keep off-diagonal entries of the Fisher information matrix small, but you can safely ignore this.) Unlike ReLU, leaky ReLU is more ?balanced,? and may therefore learn faster.
Be aware that the result is not always consistent. Leaky ReLU isn?t always superior to plain ReLU, and should be considered only as an alternative.
Exponential Linear (ELU, SELU)
Similar to leaky ReLU, ELU has a small slope for negative values. Instead of a straight line, it uses a log curve like the following:
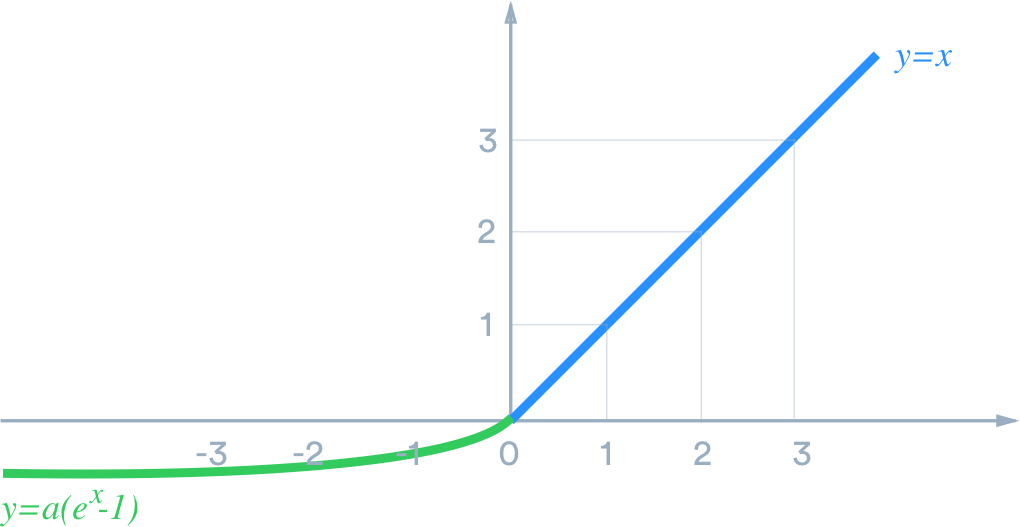
It is designed to combine the good parts of ReLU and leaky ReLU ? while it doesn?t have the dying ReLU problem, it saturates for large negative values, allowing them to be essentially inactive.
ELU was first proposed in this paper. It is sometimes called Scaled ELU (SELU) due to the constant factor a.
Concatenated ReLU (CReLU)
Concatenated ReLU has two outputs, one ReLU and one negative ReLU, concatenated together. In other words, for positive x it produces [x, 0], and for negative x it produces [0, x]. Because it has two outputs, CReLU doubles the output dimension.
CReLU was first proposed in this paper.
ReLU-6
You may run into ReLU-6 in some libraries, which is ReLU capped at 6. In other words, it looks like the following:
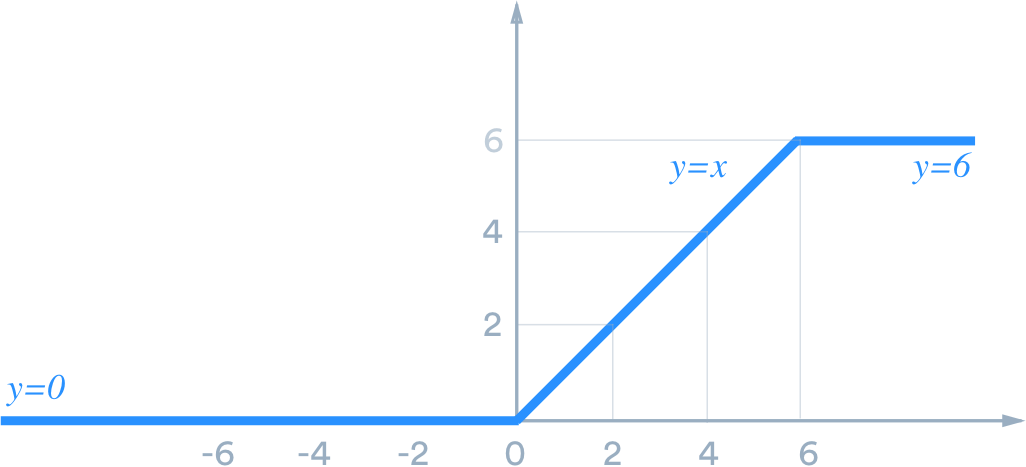
It was first used in this paper for CIFAR-10, and 6 is an arbitrary choice that worked well. According to the authors, the upper bound encouraged their model to learn sparse features earlier.
How do I use it?
ReLU and its variants come standard with most frameworks.
TensorFlow
TensorFlow provides ReLU and its variants through the tf.nn module. For example, the following creates a convolution layer (for CNN) with tf.nn.relu:
import tensorflow as tfconv_layer = tf.layers.conv2d( inputs=input_layer, filters=32, kernel_size=[5, 5], padding=’same’, activation=tf.nn.relu,)
Keras
Keras provides ReLU and its variants through the keras.layers.Activation module. The following adds a ReLU layer to the model:
from keras.layers import Activation, Densemodel.add(Dense(64, activation=’relu’))
PyTorch
PyTorch provides ReLU and its variants through the torch.nn module. The following adds 2 CNN layers with ReLU:
from torch.nn import RNNmodel = nn.Sequential( nn.Conv2d(1, 20, 5), nn.ReLU(), nn.Conv2d(20, 64, 5), nn.ReLU())
It can also be used directly:
import torchfrom torch import autograd, nnrelu = nn.ReLU()var = autograd.Variable(torch.randn(2))relu(var)
Certain PyTorch layer classes take relu as a value to their nonlinearity argument. For example, the following creates an RNN layer with ReLU:
rnn = nn.RNN(10, 20, 2, nonlinearity=’relu’)