Ready for another riddle?
The solution to this problem requires nothing more than a bit of cleverness and some very, very strategic counting.
100 prisoners are sentenced to life in prison in solitary confinement. Upon arrival at the prison, the warden proposes a deal to keep them entertained, certain that the prisoners are too dim-witted and impatient to accomplish it.
The warden has a large bowl containing the cell numbers of all the prisoners. Each day he randomly chooses one cell from the bowl, the corresponding prisoner is taken to the interrogation room, and the cell number is returned to the bowl.
While in the interrogation room, the prisoner will not be allowed to touch anything except the light switch, which the prisoner may choose to turn on or off.
The prisoner may make the assertion that all 100 prisoners have been in the room. If the prisoner?s assertion is correct, all prisoners will be released. If the prisoner is incorrect, the game is over and their chance to be freed is gone.
The prisoners are given one meeting to discuss a strategy before their communication is completely severed. What strategy should they adopt in order to ensure, with 100% certainty, that one of them will guess correctly and all be freed?
The initial state of the light is OFF when the first prisoner enters the room.
Make A Smaller Case To Examine
A valuable problem solving technique is to reduce the problem into a smaller, more manageable case.
Often the complexity of a problem comes from either scale or abstraction. By simplifying the problem we can work around these issues. Once we have a handle on the smaller case, we can use the insights we?ve gained to tackle the more difficult version.
Let?s simplify this problem down to 5 prisoners. We?ll begin by generating a few possible outcomes:
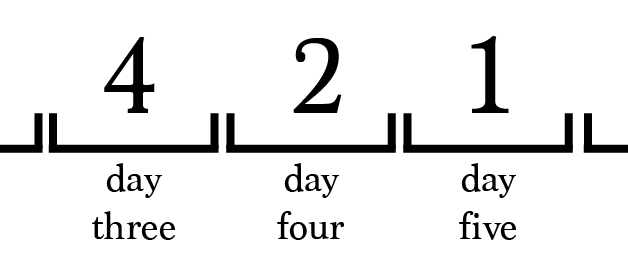
Let?s take a closer look at simulation one.
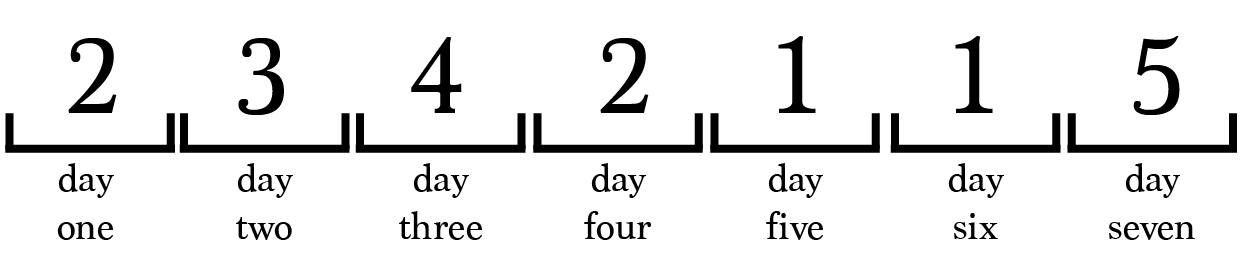
On day 1, prisoner 2 is selected to enter the interrogation room.
According to our simulation, prisoner 2 will return on day 4. When prisoner 2 returns there is no way for the prisoner to know exactly who was in the room on days 2 and 3.
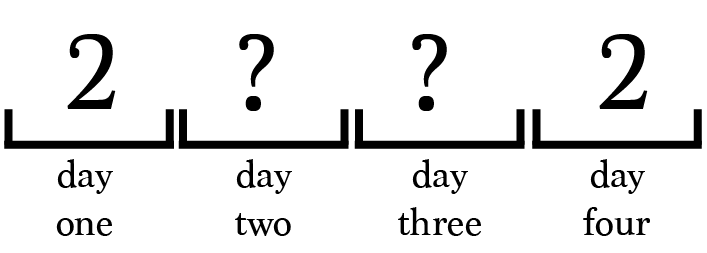
Prisoner 2 can only conclude that at least 2 different prisoners have been in the interrogation room, prisoner 2 and someone else.
Suppose prisoner 2 enters the room again on day 8.
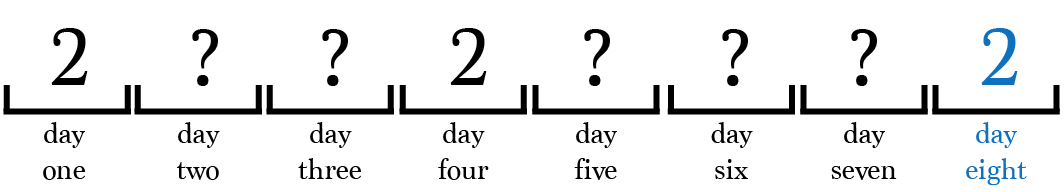
At this point, we know that prisoner 2 can correctly make the assertion, but prisoner 2 is completely unaware of this. Prisoner 2 can only safely conclude that at least 2 distinct prisoners have been in the room ? the exact same conclusion made on day four.
Hmmm this may be troubling. But of course! We haven?t used the light bulb yet.
Signaling With the Light Bulb
When prisoner 2 first enters the room, the light is off. If prisoner 2 leaves the light on, it will remain on when prisoner 3 arrives.
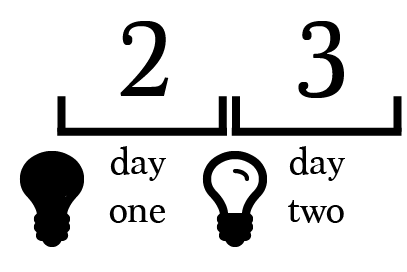
The question now is: Should prisoner 3 leave the light on or turn it off?
If the light remains on, no information is conveyed.
If prisoner 3 turns the light off and it remains off, it conveys a signal to prisoner 2.
If prisoner 3 turns the light off and prisoner 4 turns it on again, when prisoner 2 returns on day four no new information is available.
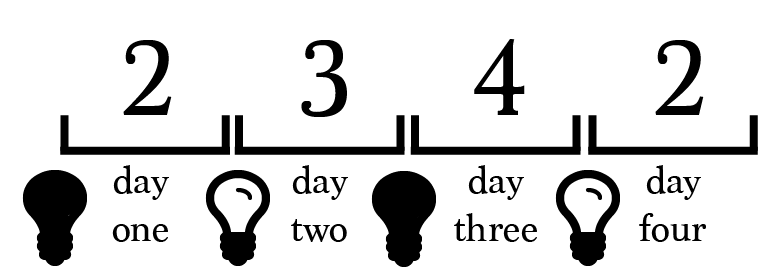
In order to convey information to prisoner 2, the light must change states only once in between prisoner 2’s visits. Any more times risks the chance the light will be on when prisoner 2 returns.
For example, we could instruct prisoner 3 to turn the light off and prisoner 4 to leave it untouched. This ensures the light is off when prisoner 2 returns.
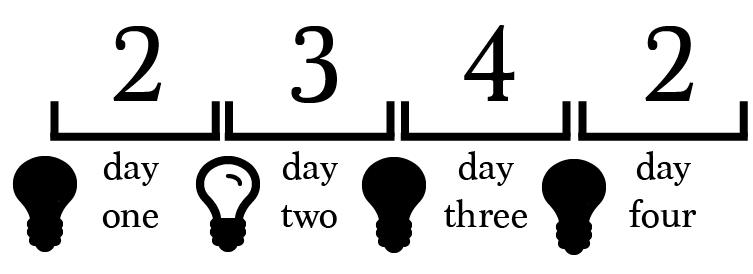
Have prisoner 2 turn the light back on to reset the system. Now let prisoner 1, the next to arrive, turn it off. The light is to remain off until prisoner 2 returns again.
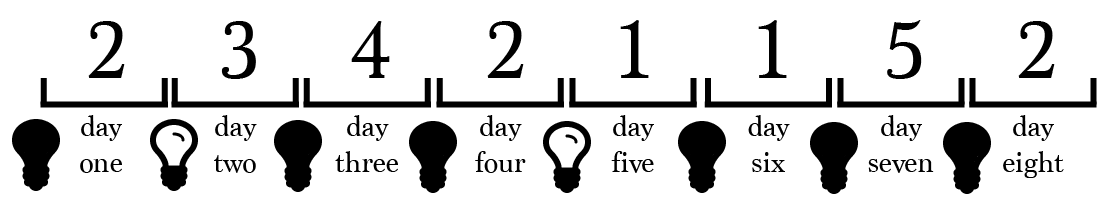
We?re getting so close to a solution? have you figured it out yet?
Suppose prisoner 3 is selected on day 9. Should we have prisoner 3 turn off the light again or leave it on this time?
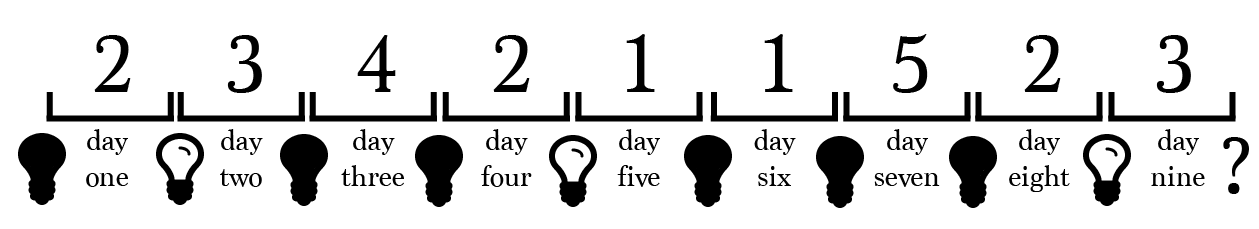
If prisoner 3 leaves the light on, prisoner 5 is free to turn it off on day 10.
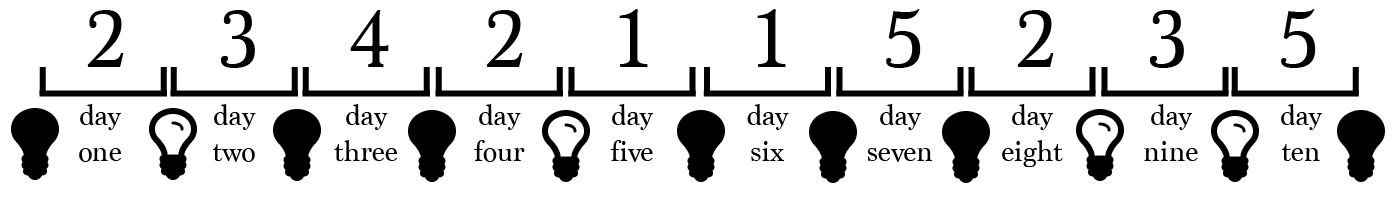diagram 2
Study the last two diagrams very carefully. In one of them lies the key to counting the prisoners. Search for a pattern between the states of the light bulbs and the prisoners. Do you see it?
Small Case Solution
Note whenever the light turns from ON to OFF in diagram 2.
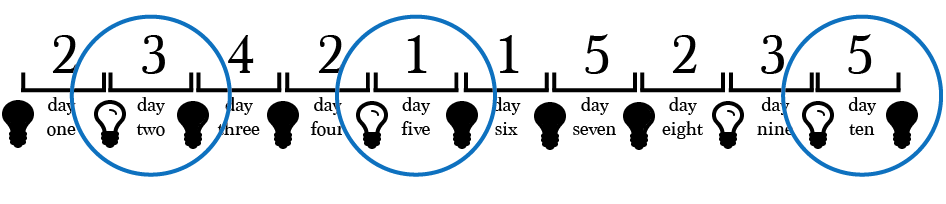diagram 2
By having all the prisoners, except prisoner 2 ? whose job is to reset the light to ON ? turn off the light only the first time they encounter it on, we create a method for counting up to one new prisoner in the room between each of prisoner 2’s visits.
If we didn?t have the stipulation that it must be the prisoner?s first time to encounter the light on, we could have ended up with diagram 1 where prisoner 3 appears twice in the blue circles. Therefore not counting distinct prisoners.
diagram 1
This can be a little confusing, so here?s a play by play.
Prisoner 2 enters the room on day 1 and turns the light ON. The next day, prisoner 3 enters and seeing the light on turns it OFF. Day 3, prisoner 4 finds the light off and leaves it OFF. Day 4, prisoner 2 returns and resets the light to ON.
On day 5, prisoner 1 enters to find the light ON for the first time and turns it OFF. On days six and seven the light is OFF and remains OFF. Day 8 it is reset again by prisoner 2. On day 9, prisoner 3 finds the light on again. Because this is the second time prisoner 3 has found the light on, prisoner 3 leaves it ON.
The next day when prisoner 5 enters the room, the light will still be ON. Prisoner 5, has not encountered the light ON before, so she turns it OFF.
On day 11, Prisoner 2 turns the light back ON. Days 12 through 18, the light remains ON since all the prisoners have been in the room with the light on before. Finally on day 19, prisoner 4 encounters the light ON for the first time and turns it OFF.
Meanwhile, prisoner 2 has been tasked with counting how many times he turned the light from OFF to ON.
As you can see below when prisoner 2 turns the light on for the 5th time, it will signal that all four other prisoners have turned the light off once. Now we can be certain everyone has been in the interrogation room.
Now that we have solved the 5 prisoner case all we need to do is generalize it for 100 prisoners.
The Final Solution
The strategy the prisoners should agree on in their meeting is:
The first prisoner selected is in charge of turning the light on whenever it is found off. Each other prisoner is to turn the light off the very first time they find it on, otherwise they are to leave it in the state they found it. When the first prisoner selected turns the light on for the 100th time, they can safely assume that all prisoners have been in the interrogation room.
These prisoners end up with a better fate than our 10 prisoners in the King?s court did!
Next Up: Amp Up Your Mental Multiplication Skills
Thanks for reading!
Please click the ? to let me know you learned something new!
