There is a short answer to this question, so let?s start there. Then we can take a look at an application to get a little more insight.
A matrix is a grid of n m (say, 3 3) numbers surrounded by brackets. We can add and subtract matrices of the same size, multiply one matrix with another as long as the sizes are compatible ((n m) (m p) = n p), and multiply an entire matrix by a constant. A vector is a matrix with just one row or column (but see below). So there are a bunch of mathematical operations that we can do to any matrix.
The basic idea, though, is that a matrix is just a 2-D grid of numbers.
A tensor is often thought of as a generalized matrix. That is, it could be a 1-D matrix (a vector is actually such a tensor), a 3-D matrix (something like a cube of numbers), even a 0-D matrix (a single number), or a higher dimensional structure that is harder to visualize. The dimension of the tensor is called its rank.
But this description misses the most important property of a tensor!
A tensor is a mathematical entity that lives in a structure and interacts with other mathematical entities. If one transforms the other entities in the structure in a regular way, then the tensor must obey a related transformation rule.
This ?dynamical? property of a tensor is the key that distinguishes it from a mere matrix. It?s a team player whose numerical values shift around along with those of its teammates when a transformation is introduced that affects all of them.
Any rank-2 tensor can be represented as a matrix, but not every matrix is really a rank-2 tensor. The numerical values of a tensor?s matrix representation depend on what transformation rules have been applied to the entire system.
This answer might be enough for your purposes, but we can do a little example to illustrate how this works. The question came up in a Deep Learning workshop, so let?s look at a quick example from that field.
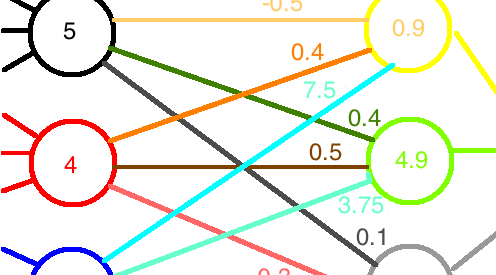
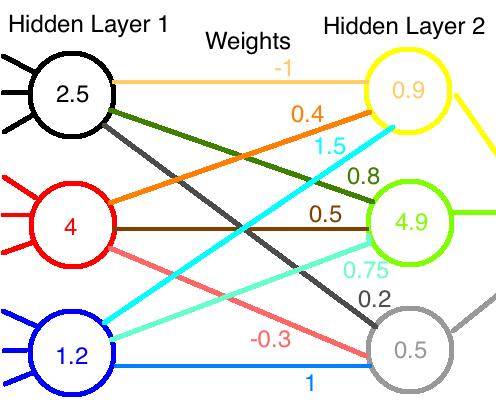
Suppose I have a hidden layer of 3 nodes in a neural network. Data flowed into them, went through their ReLU functions, and out popped some values. Let?s say, for definiteness, we got 2.5, 4, and 1.2, respectively. (Don?t worry, a diagram is coming.) We could represent these nodes? output as a vector,
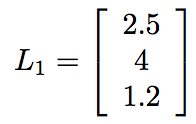
Let?s say there?s another layer of 3 nodes coming up. Each of the 3 nodes from the first layer has a weight associated with its input to each of the next 3 nodes. It would be very convenient, then, to write these weights as a 3 3 matrix of entries. Suppose we?ve updated the network already many times and arrived at the weights (chosen semi-randomly for this example),
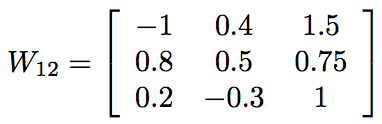
Here, the weights from one row all go to the same node in the next layer, and those in a particular column all come from the same node in the first layer. For example, the weight that incoming node 1 contributes to outgoing node 3 is 0.2 (row 3, col 1). We can compute the total values fed into the next layer of nodes by multiplying the weight matrix by the input vector,
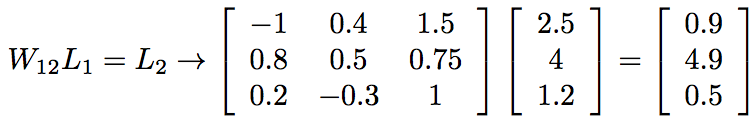
Don?t like matrices? Here?s a diagram. The data flow from left to right.
Great! So far, all we have seen are some simple manipulations of matrices and vectors.
BUT!
Suppose I want to meddle around and use custom activation functions for each neuron. A dumb way to do this would be to rescale each of the ReLU functions from the first layer individually. For the sake of this example, let?s suppose I scale the first node up by a factor of 2, leave the second node alone, and scale the third node down by 1/5. This would change the graphs of these functions as pictured below:
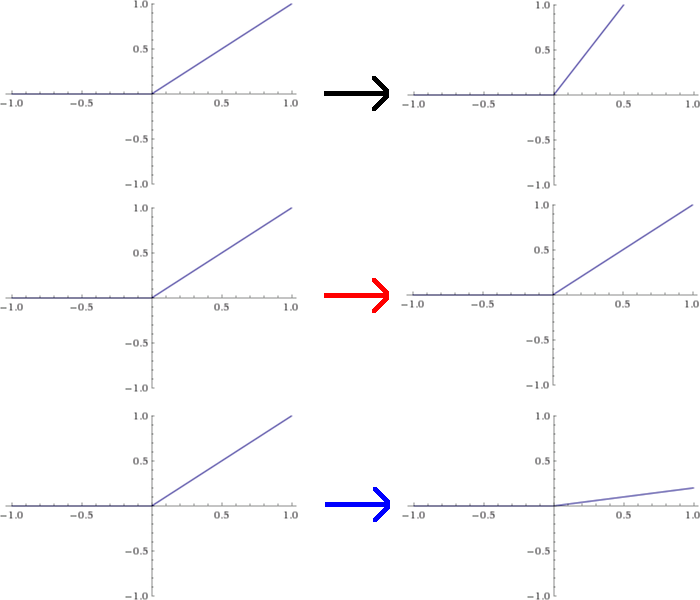
The effect of this modification is to change the values spit out by the first layer by factors of 2, 1, and 1/5, respectively. That?s equivalent to multiplying L1 by a matrix A,
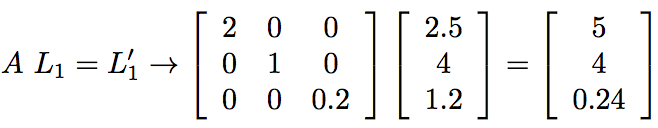
Now, if these new values are fed through the original network of weights, we get totally different output values, as illustrated in the diagram:
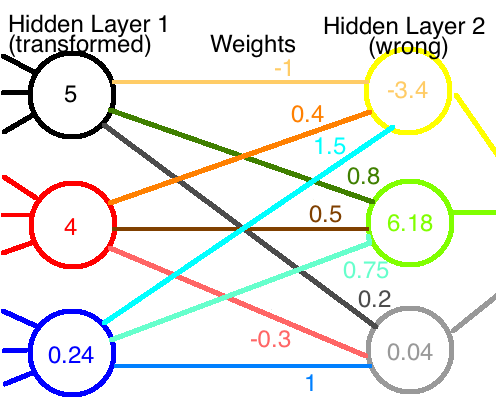
If the neural network were functioning properly before, we?ve broken it now. We?ll have to rerun the training to get the correct weights back.
Or will we?
The value at the first node is twice as big as before. If we cut all of its outgoing weights by 1/2, its net contribution to the next layer is unchanged. We didn?t do anything to the second node, so we can leave its weights alone. Lastly, we?ll need to multiply the final set of weights by 5 to compensate for the 1/5 factor on that node. This is equivalent, mathematically speaking, to using a new set of weights which we obtain by multiplying the original weight matrix by the inverse matrix of A:
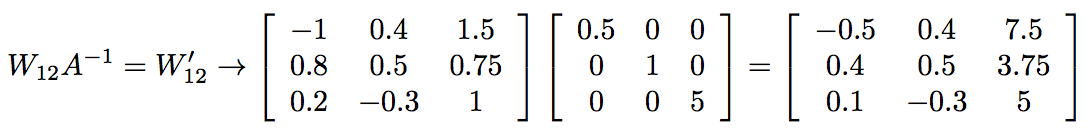
If we combine the modified output of the first layer with the modified weights, we end up with the correct values reaching the second layer:
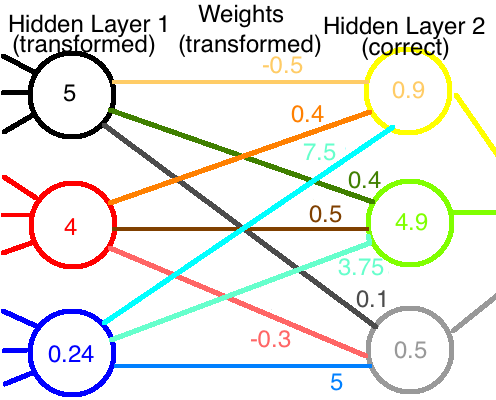
Hurray! The network is working again, despite our best efforts to the contrary!
OK, there?s been a ton of math, so let?s just sit back for a second and recap.
When we thought of the node inputs, outputs and weights as fixed quantities, we called them vectors and matrices and were done with it.
But once we started monkeying around with one of the vectors, transforming it in a regular way, we had to compensate by transforming the weights in an opposite manner. This added, integrated structure elevates the mere matrix of numbers to a true tensor object.
In fact, we can characterize its tensor nature a little bit further. If we call the changes made to the nodes covariant (ie, varying with the node and multiplied by A), that makes the weights a contravariant tensor (varying against the nodes, specifically, multiplied by the inverse of A instead of A itself). A tensor can be covariant in one dimension and contravariant in another, but that?s a tale for another day.
And now you know the difference between a matrix and a tensor.