It?s extending the unit vector idea.
Refer to famous visualisation of 3Blue1Brown?s video: Linear combinations, span, and basis vectors
R and R
R means a Real numbers 2D plane.Usually the X/Y Axes plane is this one.
R means Real numbers 3D plane.Usually the X/Y/Z Axes plane.
Linear combinations (Vector Addition)
DEFINITION: The sum of cv and dw is a linear combination of v and w.
Linear combinations means to add vectors together: v? + v? + v?….. to get a new vector. Simple like that.
Span of vectors
It?s the Set of all the linear combinations of a number vectors.
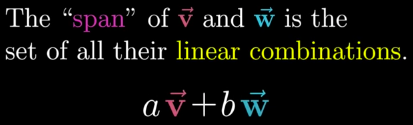# v, w are vectorsspan(v, w) = Rspan(0) = 0
One vector with a scalar, no matter how much it stretches or shrinks, it ALWAYS on the same line, because the direction or slope is not changing. So ONE VECTOR’S SPAN IS A LINE.
Two vector with scalars, we then COULD change the slope! So that we could get to any position that we want in the 2D plane, i.e., R.
Exceptions:
- span(0) = 0, it only stay at origin.
- v = w, if two vectors are the same, or collinear, then it’s still ONE vector.
Linearly dependent & independent
- Linear dependence: two vectors are COLLINEAR, means on the same line.
- Linear independence: two vectors are NOT COLLINEAR, means they’re not on the same line.
Vectors (2, 3) and (4, 6) are the SAME VECTOR! Because (4,6) = 2*(2,3), so it’s just a scaled version of the first vector.
So we say the vectors (2, 3) and (4, 6) are DEPENDENT, because they’re COLLINEAR.
Other than that, any two vectors are INDEPENDENT, if they’re not NOT COLLINEAR.
List of some linear combinations
Let?s list some vector combinations:
- Zero Vector: span(0) = 0.
- One vector: span(v) = a line.
- Two vector: span(v?, v?) = R, if they’re not collinear.
- Three vector or more: span(v?, v?, v?…) = R. Other than two vectors, are all REDUNDANT.
In another word:IF ANY TWO VECTORS ARE INDEPENDENT, THEN OTHERS ARE ALL DEPENDENT.
How to calculate a linear combination’s independency
Refer to Adam Panagos: Linear Algebra Example Problems ? Linearly Independent Vectors #1[Refer to TheTrevTutor: [Linear Algebra] Linear Independence and Bases](https://www.youtube.com/watch?v=OLqc_rt7abI)Refer to Khan lecture: Span and linear independence example
It?s important for knowing if a linear combination can fill out a plane or space. For example, if two vectors aren’t independent, then it’s just one vector, and can only draw a line. If three vectors aren’t independent, then they’re just two vectors, one is redundant, so they can only fill out a 2D plane instead of a 3D space.
A linear combination is independent, iff it could satisfy this equation:
c?v? + c?v? + c?v? …. = 0
c.. means the scalar for each vector, and you could change the scalar to any number, positive or negative.Note that: c ? 0, and vectors are not all zeros.
Assume that there?s a linear combination of two vectors v? + v? + v?, with scalars it could be c?v? + c?v? + c?v?.To verify whether it’s dependent or independent, we assume c?v? + c?v? + c?v?= (0,0,0) and solve for c?, c?, c?:
- it?s independent <=> if c? = c? = c? = 0 all are zeros
- it?s dependent <=> If c?, c?, c? at least one is NON-ZERO number
Independent Example:
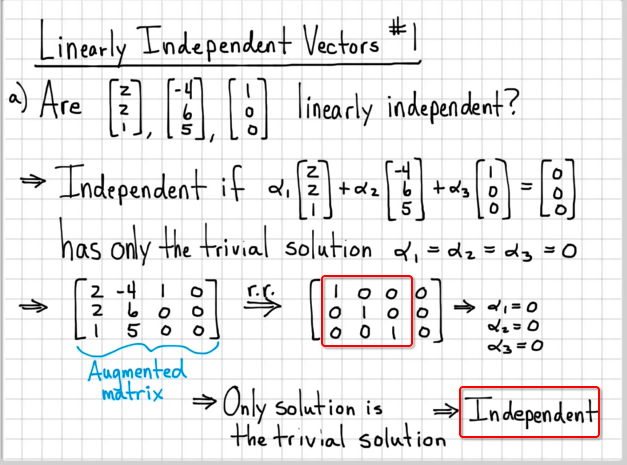
Dependent Example:
–
