Deep residual networks took the deep learning world by storm when Microsoft Research released Deep Residual Learning for Image Recognition. These networks led to 1st-place winning entries in all five main tracks of the ImageNet and COCO 2015 competitions, which covered image classification, object detection, and semantic segmentation. The robustness of ResNets has since been proven by various visual recognition tasks and by non-visual tasks involving speech and language.
This post will summarize the three papers below, with simple and clean Keras implementations of the network architectures discussed. You will have a solid understanding of residual networks and their implementation by the end of this post.
- Deep Residual Learning for Image Recognition ? ResNet (Microsoft Research)
- Wide Residual Networks (Universit Paris-Est, cole des Ponts ParisTech)
- Aggregated Residual Transformations for Deep Neural Networks ? ResNeXt (Facebook AI Research)
Lots of paraphrasing/quotes from these papers throughout this article.
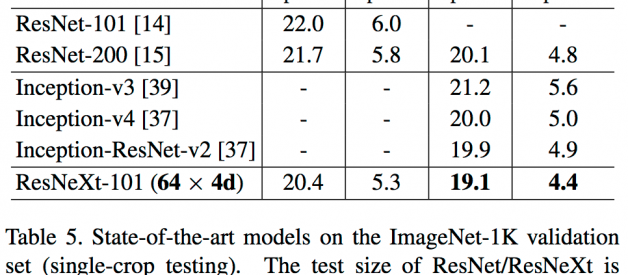
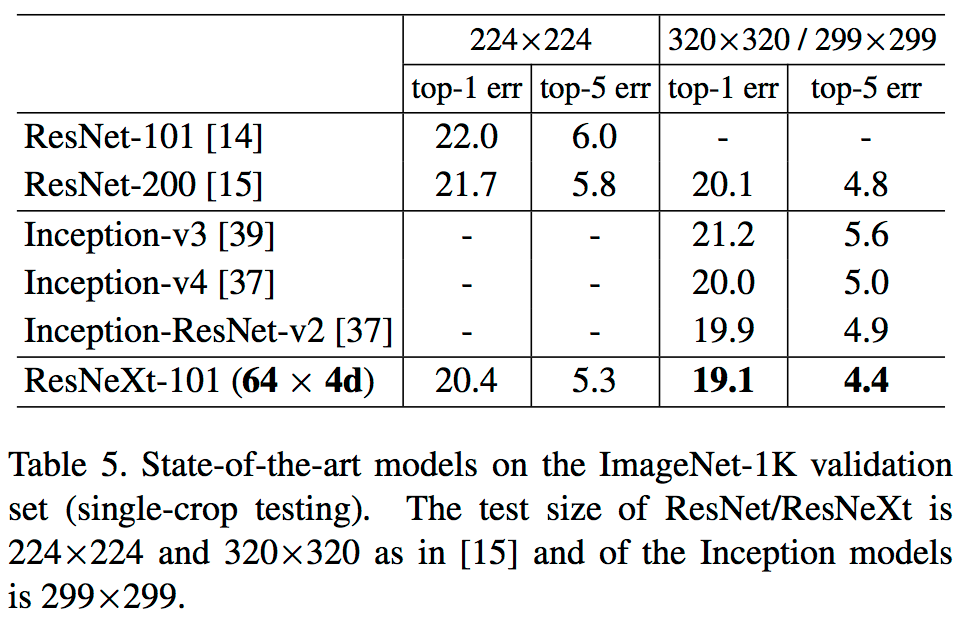ResNeXt is current state-of-the-art (2nd in the ILSVRC 2016 classification task) and much simpler than models belonging to the Inception family (which has important practical considerations). Table 5: https://arxiv.org/pdf/1611.05431.pdf
Motivation
Network depth is of crucial importance in neural network architectures, but deeper networks are more difficult to train. The residual learning framework eases the training of these networks, and enables them to be substantially deeper ? leading to improved performance in both visual and non-visual tasks. These residual networks are much deeper than their ?plain? counterparts, yet they require a similar number of parameters (weights).
The (degradation) problem:
With network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error.
The core insight:
Let us consider a shallower architecture and its deeper counterpart that adds more layers onto it. There exists a solution to the deeper model by construction: the layers are copied from the learned shallower model, and the added layers are identity mapping. The existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart.
The proposed solution:
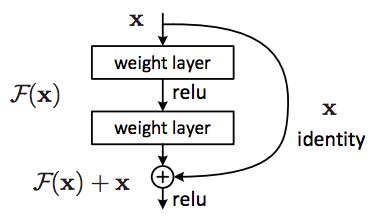A residual block ? the fundamental building block of residual networks. Figure 2: https://arxiv.org/pdf/1512.03385.pdf
Instead of hoping each stack of layers directly fits a desired underlying mapping, we explicitly let these layers fit a residual mapping. The original mapping is recast into F(x)+x. We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
We have reformulated the fundamental building block (figure above) of our network under the assumption that the optimal function a block is trying to model is closer to an identity mapping than to a zero mapping, and that it should be easier to find the perturbations with reference to an identity mapping than to a zero mapping. This simplifies the optimization of our network at almost no cost. Subsequent blocks in our network are thus responsible for fine-tuning the output of a previous block, instead of having to generate the desired output from scratch.
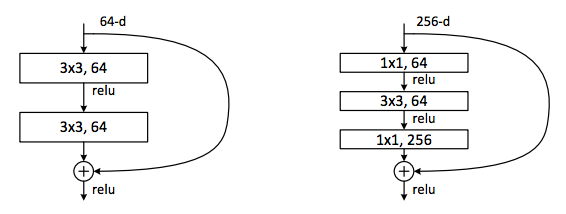A bottleneck residual block (right) makes residual networks more economical (used hereinafter) but accomplishes the same purpose as the basic residual block (left). Figure 5: https://arxiv.org/pdf/1512.03385.pdf
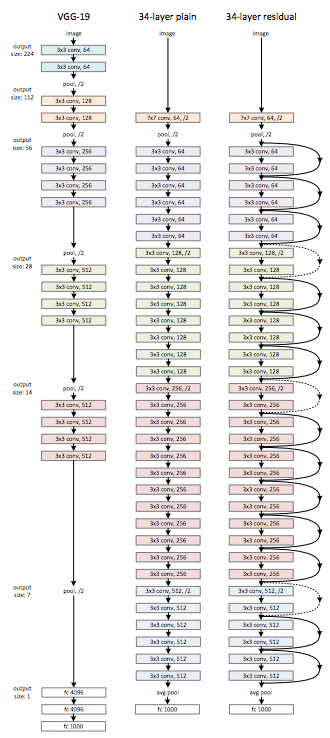Residual network compared to VGG and plain networks. Dashed lines in the identity shortcut correspond to line 19 in the ?Keras implementation of a residual block? code snippet above. Figure 3: https://arxiv.org/pdf/1512.03385.pdf
Wide Residual Networks
Wide (width refers to the number of channels in a layer) residual networks attempt to address the problem of diminishing feature reuse (few residual blocks learning useful representations or many blocks sharing very little information with small contribution to the final goal) in very deep (thin) residual networks.
The key insight of this paper is that the main power of deep residual networks is in residual blocks, and that the effect of depth is actually supplementary (contrary to what was believed).
We will take this insight and skip over their proposed architecture as the performance improvements they achieve seem to be due to increased model capacity (number of parameters) and adding additional regularization in the form of dropout ? not the actual architecture. We will see in the next section (ResNeXt) that there is a much more effective way to increase model capacity than just increasing width. In fact, there is a balance between the depth and width of these networks ? if layers are too wide the model will learn extraneous information (added noise), and if layers are too thin subsequent layers will not have much to learn from (i.e. diminishing feature reuse).
It is worth noting that training time is reduced because wider models take advantage of GPUs being more efficient in parallel computations on large tensors even though the number of parameters and floating point operations has increased.
ResNeXt
In Deep Residual Learning for Image Recognition a residual learning framework was developed with the goal of training deeper neural networks. Wide Residual Networks showed the power of these networks is actually in residual blocks, and that the effect of depth is supplementary at a certain point. Aggregated Residual Transformations for Deep Neural Networks builds on this, and exposes a new dimension called cardinality as an essential network parameter, in addition to depth and width. Cardinality is demonstrated to be more effective than going deeper or wider when increasing model capacity, especially when increasing depth and width leads to diminishing returns.
Aggregated Residual Transformations for Deep Neural Networks observes that an important common property of Inception family models is a split-transform-merge strategy. In an Inception module, the input is split into a few lower ? dimensional embeddings (by 11 convolutions), transformed by a set of specialized filters (33, 55, etc?), and merged by concatenation. It can be shown that the solution space of this architecture is a strict subspace of the solution space of a single large layer (e.g., 55) operating on a high-dimensional embedding. The split-transform-merge behavior of Inception modules is expected to approach the representational power of large and dense layers, but at a considerably lower computational complexity.
However, Inception models are accompanied with a series of complicating factors ? the filter numbers and sizes are tailored for each individual transformation, and the modules are customized stage-by-stage. Although careful combinations of these components yield excellent neural network recipes, it is in general unclear how to adapt the Inception architectures to new datasets/tasks, especially when there are many factors and hyper-parameters to be designed.
ResNeXt is a simple architecture which adopts VGG/ResNets? strategy of repeating layers, while exploiting Inceptions? split-transform-merge strategy in a simple, extensible way. A module in ResNeXt performs a set of transformations (cardinality is the size of the set of transformations), each on a low-dimensional embedding, whose outputs are aggregated by summation. The transformations to be aggregated are all of the same topology. This design allows us to extend to any large number of transformations without specialized design.
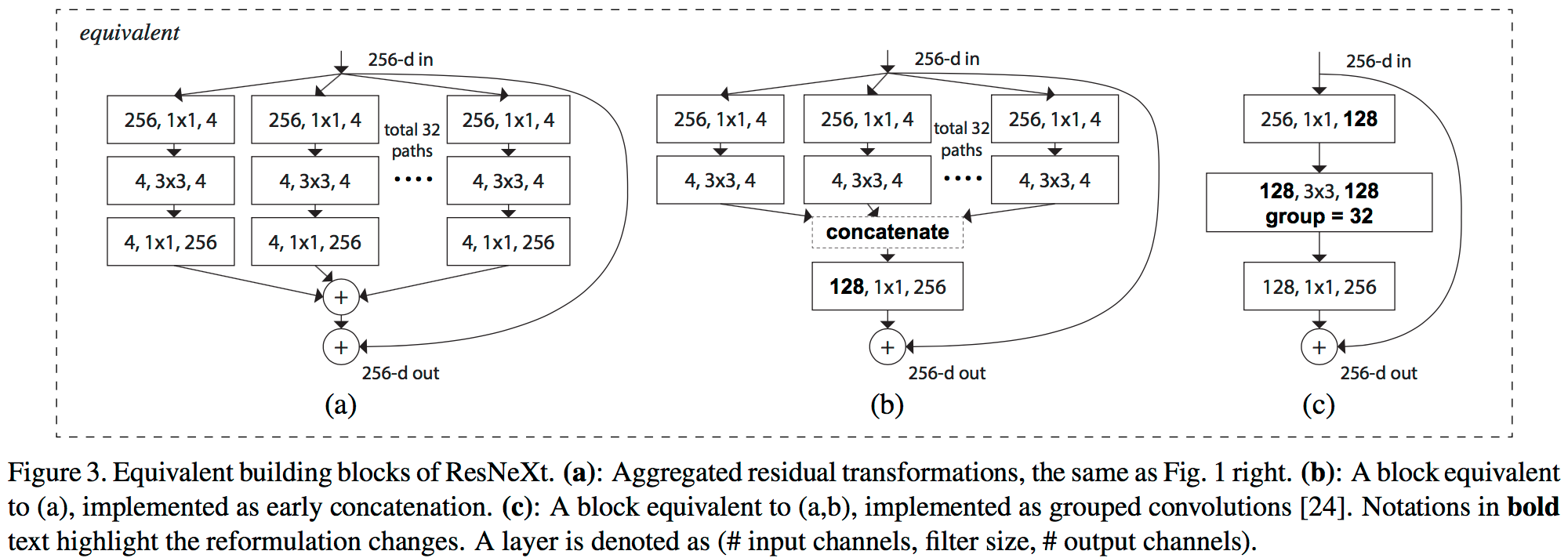A residual split-transform-merge block ? the fundamental building block of ResNeXt. Figure 3: https://arxiv.org/pdf/1611.05431.pdf
Residual connections are helpful for simplifying a network?s optimization, whereas aggregated transformations lead to stronger representation power (as shown by the fact that they perform consistently better than their counterparts with or without residual connections).
The result is a homogenous, multi-branch architecture with only a few hyper-parameters to set.
Keras implementation of ResNeXt (ResNet in the case where `cardinality` == 1)
Please comment on Gist if you spot any errors/possible improvements in code. pyt?rch implementation.
I?ll be working ResNeXt into my improved Wasserstein GAN code (wGAN implemented on top of keras/tensorflow as described in: Wasserstein GAN with improvements as described in: Improved Training of Wasserstein GANs) and running some experiments (i.e. a pre-trained discriminator). Expect a blog post on this in the near future.
Here is a rough draft of a GAN network architecture where generator and discriminator are ResNeXt. Please comment on Gist if you spot any errors/possible improvements. https://gist.github.com/mjdietzx/600751b780e1ab2b8802f7788f17882e
wayaai/GAN-Sandbox
GAN-Sandbox – wGAN branch ? Wasserstein GAN implemented on top of keras/tensorflow with improvements to objective function (penalizing norms of gradients).
github.com
I?ll be talking about GANs at the Deep Learning in Healthcare Summit in Boston on Friday, May 26th. Feel free to stop by and say ?!
