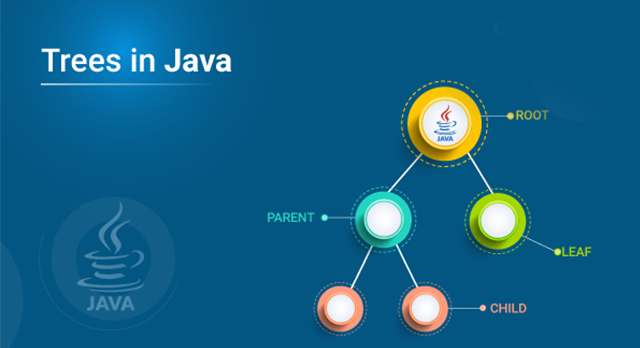
 Trees in Java ? Edureka
Trees in Java ? Edureka
If I had to pick the single most important topic in software development, it would be data structures. One of the most common and easiest ones is a tree ? a hierarchical data structure. In this article, let?s explore Trees in Java.
- What is a Binary Tree?
- Types of Binary Tree
- Binary Tree Implementation
- Tree Traversals
- Applications of Binary Tree
What is a Binary Tree?
A is a non-linear data structure where data objects are generally organized in terms of hierarchical relationship. The structure is non-linear in the sense that, unlike Arrays, Linked Lists, Stack and Queues, data in a tree is not organized linearly. A binary tree is a recursive tree data structure where each node can have 2 children at most.
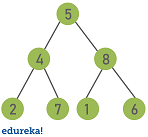
Binary trees have a few interesting properties when they?re perfect:
- Property 1: The number of total nodes on each ?level? doubles as you move down the tree.
- Property 2: The number of nodes on the last level is equal to the sum of the number of nodes on all other levels, plus 1
Each data element stored in a tree structure called a node. A Tree node contains the following parts: 1. Data
2. Pointer to left child
3. Pointer to the right child
In Java, we can represent a tree node using class. Below is an example of a tree node with integer data.
static class Node { int value; Node left, right; Node(int value){ this.value = value; left = null; right = null; }
Now that you know what is a binary tree, let?s check out different types of binary trees.
Types of Binary Trees
Full Binary Tree
A full binary tree is a binary tree where every node has exactly 0 or 2 children. The example of fully binary tress is:
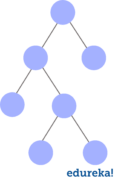
Perfect Binary Tree
A binary tree is perfect binary Tree if all internal nodes have two children and all leaves are at the same level. The example of perfect binary tress is:
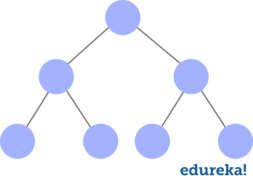
Complete Binary Tree
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. An example of a complete binary tree is:
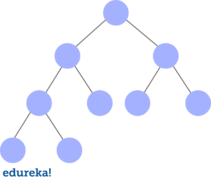
Now that you are aware of different types of binary trees, let?s check out how to create a binary tree.
Binary Tree Implementation
For the implementation, there?s an auxiliary Node class that will store int values and keeps a reference to each child. The first step is to find the place where we want to add a new node in order to keep the tree sorted. We?ll follow these rules starting from the root node:
- if the new node?s value is lower than the current node?s, go to the left child
- if the new node?s value is greater than the current node?s, go to the right child
- when the current node is null, we?ve reached a leaf node, we insert the new node in that position
Now let?s see how we can implement this logic with the help of an example:
package MyPackage; public class Tree { static class Node { int value; Node left, right; Node(int value){ this.value = value; left = null; right = null; } } public void insert(Node node, int value) { if (value < node.value) { if (node.left != null) { insert(node.left, value); } else { System.out.println(” Inserted ” + value + ” to left of ” + node.value); node.left = new Node(value); } } else if (value > node.value) { if (node.right != null) { insert(node.right, value); } else { System.out.println(” Inserted ” + value + ” to right of ” + node.value); node.right = new Node(value); } } } public void traverseInOrder(Node node) { if (node != null) { traverseInOrder(node.left); System.out.print(” ” + node.value); traverseInOrder(node.right); } } public static void main(String args) { Tree tree = new Tree(); Node root = new Node(5); System.out.println(“Binary Tree Example”); System.out.println(“Building tree with root value ” + root.value); tree.insert(root, 2); tree.insert(root, 4); tree.insert(root, 8); tree.insert(root, 6); tree.insert(root, 7); tree.insert(root, 3); tree.insert(root, 9); System.out.println(“Traversing tree in order”); tree.traverseLevelOrder(); }}
Output:
Binary Tree ExampleBuilding tree with root value 5 Inserted 2 to left of 5 Inserted 4 to right of 2 Inserted 8 to right of 5 Inserted 6 to left of 8 Inserted 7 to right of 6 Inserted 3 to left of 4 Inserted 9 to right of 8Traversing tree in order 2 3 4 5 6 7 8 9
In this example, we have used in-order traversal to traverse the tree. The in-order traversal consists of first visiting the left sub-tree, then the root node, and finally the right sub-tree. There are more ways to traverse a tree. Let?s check them out.
Tree Traversals
Trees can be traversed in several ways: Let?s use the same tree example that we used before for each case.
Depth First Search
Depth-first search is a type of traversal where you go as deep as possible down one path before backing up and trying a different one. There are several ways to perform a depth-first search: in-order, pre-order and post-order.
We already checked out in-order traversal. Let?s check out pre-order and post-order now.
Pre-Order Traversal
In Pre-order traversal you visit the root node first, then the left subtree, and finally the right subtree. Here?s the code.
public void traversePreOrder(Node node) { if (node != null) { System.out.print(” ” + node.value); traversePreOrder(node.left); traversePreOrder(node.right); }}
Output:
5 2 4 3 8 6 7 9
Post-Order Traversal
In Post-order traversal you visit left subtree first, then the right subtree, and the root node at the end. Here?s the code.
public void traversePostOrder(Node node) { if (node != null) { traversePostOrder(node.left); traversePostOrder(node.right); System.out.print(” ” + node.value); }}
Output:
3 4 2 7 6 9 8 5
Breadth-First Search
This type of traversal visits all the nodes of a level before going to the next level. It is like throwing a stone in the center of a pond. The nodes you explore ?ripple out? from the starting point. Breadth-First Search is also called level-order and visits all the levels of the tree starting from the root, and from left to right.
Applications of Binary Tree
Applications of binary trees include:
- Used in many search applications where data is constantly entering/leaving
- As a workflow for compositing digital images for visual effects
- Used in almost every high-bandwidth router for storing router-tables
- Also used in wireless networking and memory allocation
- Used in compression algorithms and many more
This brings us to the end of this ?Trees in Java? article.
Make sure you practice as much as possible and revert your experience.
If you wish to check out more articles on the market?s most trending technologies like Artificial Intelligence, DevOps, Ethical Hacking, then you can refer to Edureka?s official site.
Do look out for other articles in this series which will explain the various other aspects of Java.
1. Object Oriented Programming
2. Inheritance in Java
3. Polymorphism in Java
4. Abstraction in Java
5. Java String
6. Java Array
7. Java Collections
8. Java Threads
9. Introduction to Java Servlets
10. Servlet and JSP Tutorial
11. Exception Handling in Java
12. Advanced Java Tutorial
13. Java Interview Questions
14. Java Programs
15. Kotlin vs Java
16. Dependency Injection Using Spring Boot
17. Comparable in Java
18. Top 10 Java frameworks
19. Java Reflection API
20. Top 30 Patterns in Java
21. Core Java Cheat Sheet
22. Socket Programming In Java
23. Java OOP Cheat Sheet
24. Annotations in Java
25. Library Management System Project in Java
26. Java Tutorial
27. Machine Learning in Java
28. Top Data Structures & Algorithms in Java
29. Java Developer Skills
30. Top 55 Servlet Interview Questions
31. Top Java Projects
32. Java Strings Cheat Sheet
33. Nested Class in Java
34. Java Collections Interview Questions and Answers
35. How to Handle Deadlock in Java?
36. Top 50 Java Collections Interview Questions You Need to Know
37. What is the concept of String Pool in Java?
38. What is the difference between C, C++, and Java?
39. Palindrome in Java- How to check a number or string?
40. Top MVC Interview Questions and Answers You Need to Know
41. Top 10 Applications of Java Programming Language
Originally published at https://www.edureka.co on September 3, 2019.

