Six Difficult Ways of Becoming a Millionaire
Want to win a million bucks? Just solve one of these problems. No strings attached. Ok maybe one string: the problems are somewhat hard. Scratch that, really hard.
The Gauntlet is Thrown
At the start of the millenium, the Clay Mathematics Institute put forward these seven problems which are deemed as some of the most difficult problems that remain open. Each problem has a one million dollar bounty for the first person to provide a valid proof (or disproof).
I have been wanting to write this article for quite some time, but struggled to decide at what level I should present the material. After a lot of umming and ahing I decided to present it at an elementary university level. A few things will be assumed (like knowledge of groups and complex plane) but everything that I think is ?new? will be explained.
At the time I am writting this, only the Poincar conjecture has been solved. Grigori Perelman presented the proof in 2003 and he was officially awarded the Millenium Prize in 2010 which he declined.
I will be presenting this conjecture (now theorem) first and then the remaining unsolved problems in order of increasing complexity.
Poincar Conjecture
Every closed, simply connected, 3-manifold is homeomorphic to the 3-sphere.
Let?s break this down word by word. Firstly, a manifold is an object or a generalisation of a space that is locallylikeEuclideanspace. This means that if you zoom in on it, it looks like a line or a plane or regular 3-dimensional space or so on? An example of a manifold would be a sphere (like the surface of a ball). If you zoom in close enough, it looks flat. The dimension of a manifold is the dimension of the space that it locally looks like, for example, a ball locally looks like a plane which means it has dimension 2, a circle locally looks like a line and so it has dimension 1. For a manifold of dimension n, we sometimes write it as an n-manifold, similarly for a specific shape like a sphere which can be generalised to n dimenions, we write it as the n-sphere.
A manifold is closed if it has no boundary and is bounded, that is it doesn?t go off to infinity (technically a manifold is closed if it doesn?t have a boundary and is compact ? but if the manifold is immersed in Euclidean n-space then given boundaryless, compact just requires being bounded). A line between 0 and 1 has a boundary at 0 and at 1 and so is not closed. A circle has no boundary and so is closed.
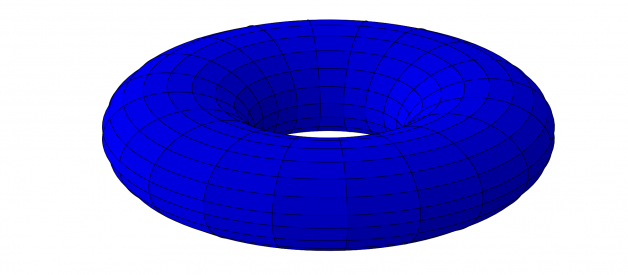
Closed 2-manifold ? this particular one is called a 2-torus
A manifold is simply connected if it has no ?holes?:
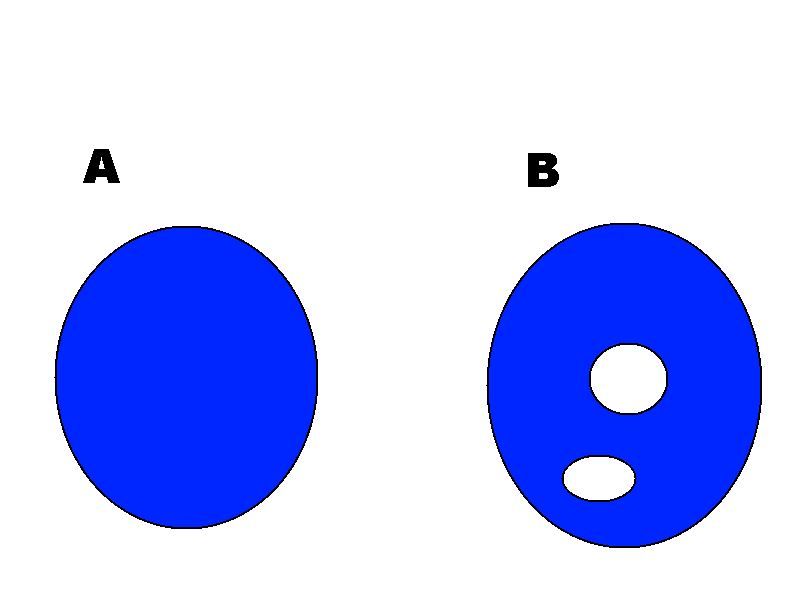(A) is a simply connected space (B) is not simply connected
An equivalent formulation of being simply-connected is that each loop can be continuously tightened to a point.
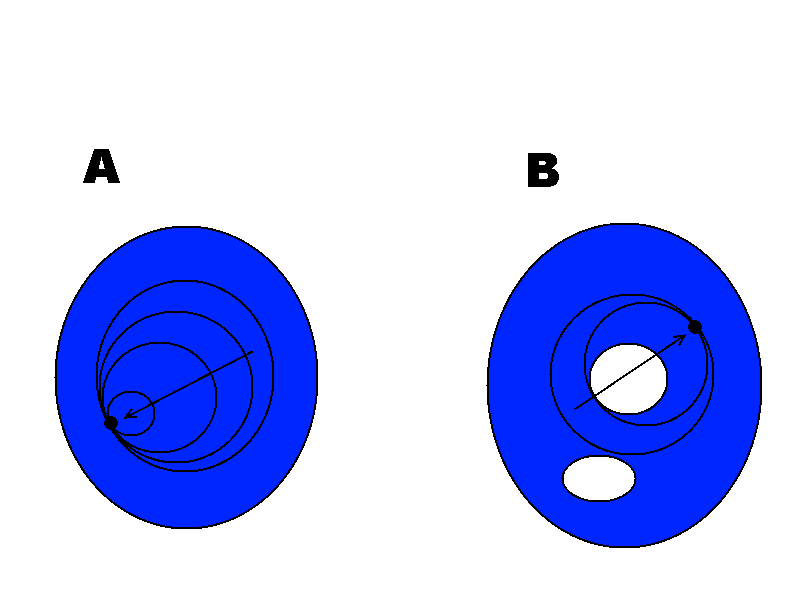(A) a loop in A can be tightened to a point (B) here a loop in B gets ?caught? on a hole and can?t be tightened to a point
Two manifolds are homeomorphic if you can deform one into the other and back again continously. Permissable deformations include stretching, squeezing and twisting, but not ripping, tearing and puncturing. This leads to the famous equivalence between a dougnut and a mug.
How to deform a doughnut into a mug
In topology, we want to classify all manifolds into classes where all manifolds within a certain class are all homeomorphic to each other.
In two dimensions, it is (somewhat) easy to see that if a manifold is closed and without holes then it is equivalent to a sphere. As it turns out, this is sufficient to determine whether a 2-manifold is homeomorphic to the sphere (2-sphere).
Poincar hypothesised at the start of the 20th century that this is true also in three dimensions, that is any closed, simply connected 3-manifold is homeomorphic to the 3-sphere.
In 2002, Grigori Perelman proved this to be true by using techniques such as Ricci flow and manifold surgery.
P vs NP
Can every problem whose solution can be verified quickly, be solved quickly?
Problems can be categorised into different complexity classes. Here we are interested in the classes P and NP. These stand for Polynomial time and Non-deterministic Polynomial time, respectively.
In essence, a P problem can solved ?quickly? and verified ?quickly?. Whereas an NP problem (currently) does not have a ?quick? solution. More specifically, given a problem with an input of size n, the time taken to solve it if it were in the P class grows according to some polynomial. Whereas if it is NP then it will grow faster.
An example of a problem that is thought to be NP (I say thought since it hinges on the verity of the hypothesis) is the (decision problem version of the) travelling salesman problem:
Given a list of cities and the distance between each, can you construct a route that visits each city whose total length is less than a given distance?
Solving this problem is hard and very taxing to solve but a solution is easy to check ? a solution is a list of cities to visit in order, and one can verify that it is a valid solution just by adding up the distances and comparing it to the given bound. It is important to note that increasing the length of the list of cities will make the time to solve much faster than any polynomial.
On the other hand, an example of a P problem is verifying if a number is in a given list. It is easy to solve and easy to check, and if you double the size of the list, the time taken will also double (so the time taken doesn?t grow too fast).
What the P vs NP problem asks is if in fact NP problems are distinct from P problems. Otherwise framed, does there exist some secret or hidden algorithm that can solve previously considered hard problems quickly?
Navier?Stokes Existence and Smoothness
In three space dimensions and time, given an initial velocity, does there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier?Stokes equations?
The Navier-Stokes equations are two non-linear partial differential equations that describe fluid motion in 3D. It is a set of two equations that link the velocity vector field and its rate of change with the pressure field, external forces applied to the liquid. The equations are written as such:
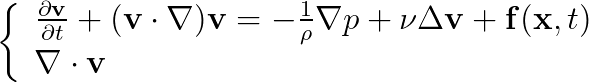
We won?t delve into what each term means but essentially, the first equation is the (viscous) fluids version of Newton?s F=ma ? the forces contributing are the sum of pressure, viscous stress and external forces. The second equation is very simply a conservation of mass and requires that the fluid is incompressible.
For a solution to be ?valid? we have two conditions:
- The vector field v and scalar field p are globally defined and continuous over the whole space.
- The total kinetic energy is bounded. (The integral of the norm squared of v over the whole space is bounded.)
So the Navier-Stokes problem is boiled down to proving one of two cases:
The affirmative: given f = 0 and an initial velocity field (that has to satisfy certain conditions) there exists a velocity and pressure field that satisfies (1) and (2).
The breakdown: There exists an initial vector field and external force field where there is no solution that satisfies (1) and (2).
N-S equations govern the diffusion of milk in tea ? Photo by Alex Boyd on Unsplash
Riemann Hypothesis
Do all non-trivial zeros of the Riemann zeta function have real part equal to 1/2?
Again, let us break this down. Firstly the Riemann zeta function is defined by the following equation
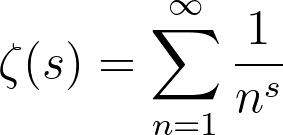
which is valid for s > 1. Note that for s = 1, the function reduces to the harmonic series which blows up. We can do some fancy maths to analytically continue (essentially extend) the function to the complex plane (apart from at s = 0 and 1) with the following functional relationship:
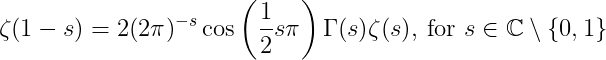
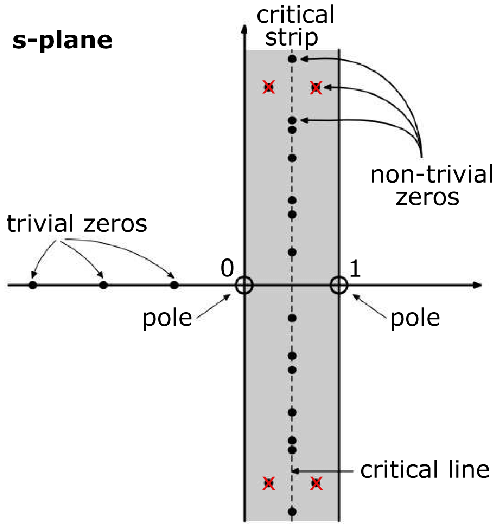
Now we want to find for which s, ?(s) = 0. Now since cosine is 0 for odd negative integers, ?(-2n) for positive integer n is 0. These are called trivial zeros since it is zero due to the nature of cosine. Instead, we are interested in when ? is zero of its own accord.
It is known that all non-trivial zeros have real part between 0 and 1, known as the critical strip. As it turns out, it seems that if s is a non-trivial zero (i.e. if ?(s) = 0 and s is not a negative even number) then s = 1/2 + iy for some value y. i.e. the real part of s is 1/2 this is known as the critical line.
Birch and Swinnerton-Dyer Conjecture
Given an elliptic curve E over ?, does the algebraic rank always coincide with the analytic rank?
An elliptic curve E, is the set of solutions of an equation of the form y=x+Ax+B with the constraint that the discriminant ?=-16(4A + 27B) ?0. The constraint just ensures that the curve is sufficiently nice.
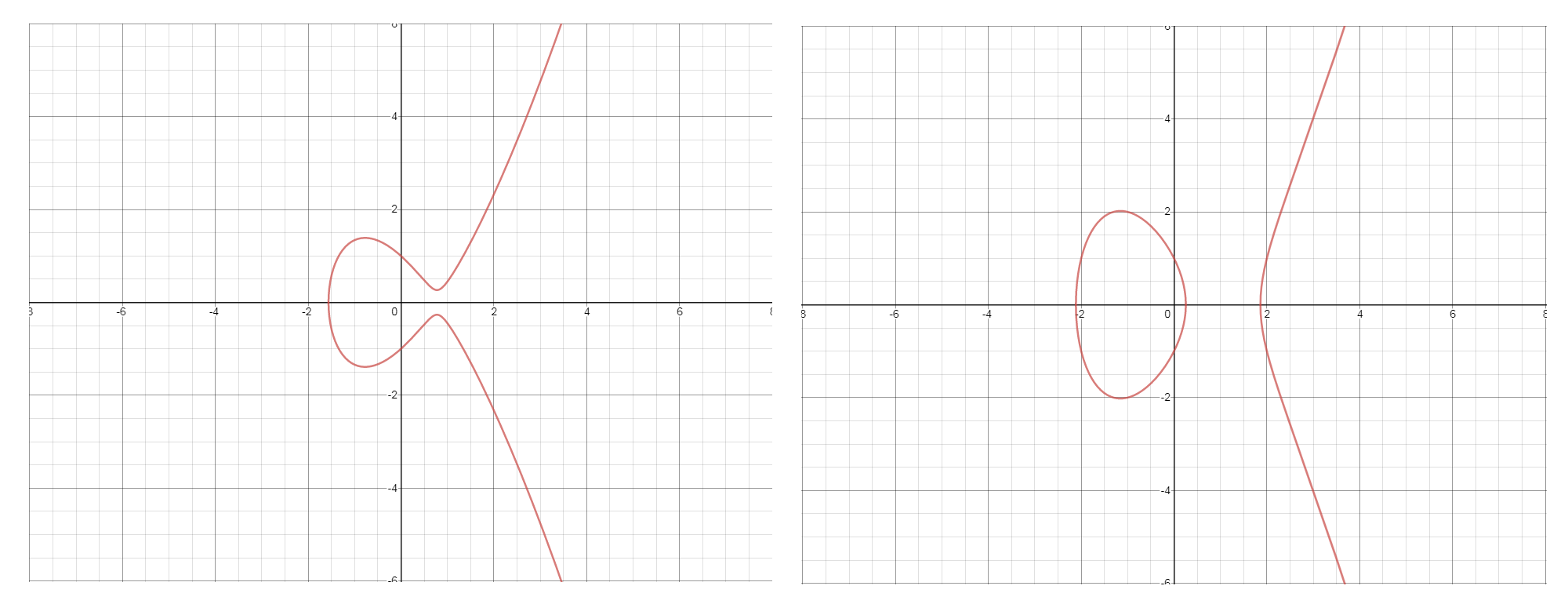Two elliptic curves. Left: y = x-1.5x+1, right: y=x-4x+1
We now restrict the solutions to the elliptic curve by requiring that x and y be rational. This is what we mean by a curve over ?. Now we can use this curve E to form a group denoted E(?). We a pretty neat binary operation: given two points, we draw a line through them, find the third intersection with E and reflect it through the x-axis.
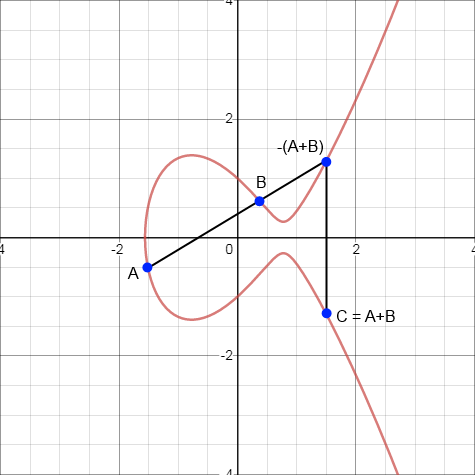How to add two points A and B to find C
In order to fully make it a group, we need to add a point at infinity which acts as the identity of the group (for the reader that is familiar with projective geometry, E is a non-singular projective curve so we get the identity for free from the ambiant space).
The first natural question to ask is what can we deduce about the structure of E(?)?
A result due to Mordell and Weil tells us that E(?) is finitely generated and can be written as
Where E(?)_tors is all the points in E(?) that have finite order. r is known as the algebraic rank of the curve E.
Great, now we have the first half. Now we need to understand the analytic rank.
Let us now restrict the solutions even further be considering E over the finite field of size p where p is a prime number
We define the following values
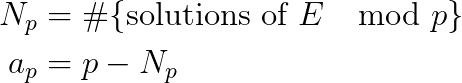
and then finally the L-series of E at s as such
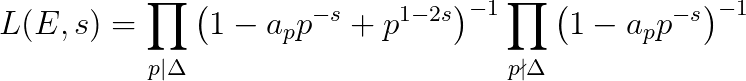
recall that ? is the discriminant of the elliptic curve. Then we can expand L as a Taylor series around s = 1:
Here, r_an is the analytic rank of the curve. Those familiar with complex analysis will recognise r_an as the vanishing order of the zero.
At long last! We can write the Birch and Swinnerton-Dyer conjecture very simply as
Ok so what does this all mean? As it turns out, computing the algebraic rank is quite hard whereas the analytic rank is somewhat easier. This conjecture provides a bridge between the land of analysis and the land of algebra.
Yang?Mills Existence and Mass Gap
Given any compact simple gauge group G, does there exist a non-trivial quantum Yang?Mills theory on ?? that has a mass gap ? > 0?
A quick disclaimer here: I am hardly an expert in particle physics so I will give my best superficial understanding here.
What this problem is asking is to make modern physics mathematically rigourous.
We start off with the idea of gauge symmetries: these are essentially freedoms in how we describe a physical system. For example, it makes no difference how and where we orient our coordinate system.
A neat theorem due to Emmy Noether is that for every symmetry, there is a corresponding conservation law. For example:
- Time invariance (i.e. it doesn?t matter if you start your experiment now or in 5 minutes after you?ve had a cup of tea) gives rise directly to the conservation of energy
- Translational invariance gives rise to conservation of momentum
Next, moving on to Yang-Mills theory.
The best explanaition I could find is given by Lawrence Krauss. Imagine a chess board, if you swap every white square for a black square and every black square for a white one, then the game is pretty much identical. Not much has happened but there has been a change so that is quite a simple symmetry.
Imagine now however that I locally switch the colour of a certain square, and do so as much as I want throughout the board. The board will look very strange but I can write a rule book that has accounted for all the swaps I?ve made. This rule book then dictates how the game is played.
Now the rule book is in fact a field and the game is a Yang-Mills theory and swaping the colours locally is a gauge symmetry.
Photo by Hassan Pasha on Unsplash
So, let?s go over it:
A gauge group is a group of (possibly very bizzare) symmetries of a system, this gives rise to a conservation law and we can write a ?rule book? that is a field that defines how particles interact which is a Yang-Mills theory.
This has already been done in the case of the electromagnetic force and the strong nuclear force which are completely described using quantum electrodynamics and quantum chromodynamics.
What the Yang-Mills Existance (we will get to mass gap in a second) asks is, does this description exist for all the four fundamental forces? And more interestingly, can they be unified?
Photo by israel palacio on Unsplash
On to mass gap: an excitation in one of these fields is actually a particle. A mass gap is essentially a stipulation that the mass of these particles have to be bounded below, so that you can?t find a particle that is arbitrarily light. This is what we observe in nature. It is called a mass gap since there is a gap between 0 and the lightest particle.
So for a Yang-Mills theory to be ?good? at describing reality must also exhibit this mass gap.
Hodge Conjecture
Let X be a non-singular complex projective manifold. Then can every Hodge class on X be written as a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X?
This one is a doozy. I?m going to go into a lot less detail here because blimey it is hard to understand.
There is a natural interchange between algebraic equations and geometrical figures. Solutions to x+y-1= 0 forms a circle and x+y-1=0 forms a line.
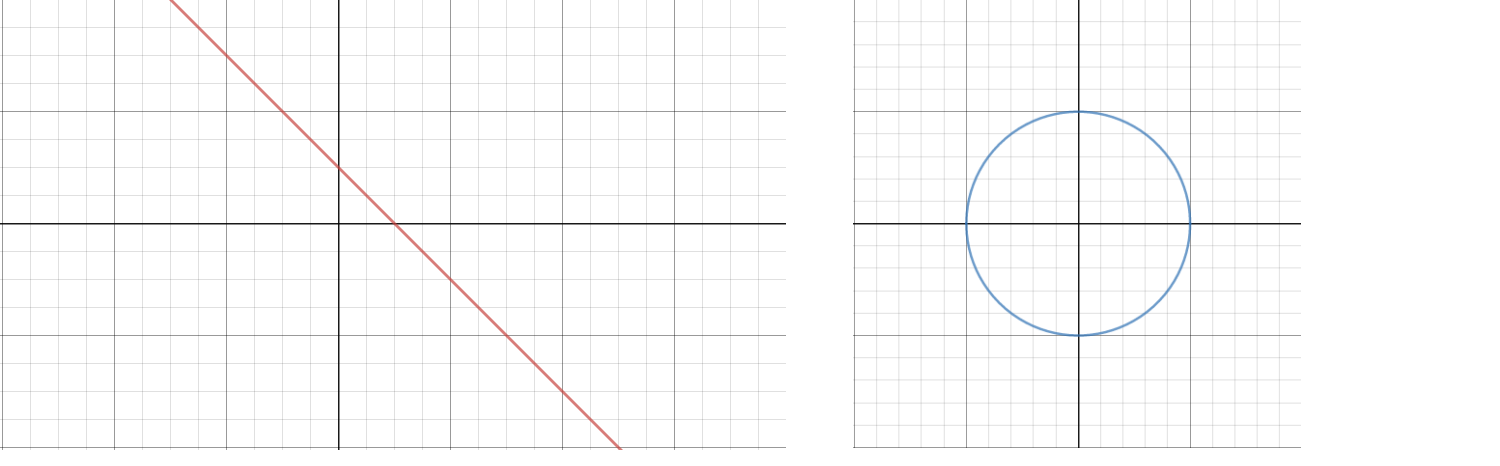
So we can come up with some crazy equations and the solution form a (sometimes very complicated) shape, these are called algebraic cycles. If these algebraic cycles are smooth enough then they can be called manifolds (recall these from the Poincar conjecture).
So algebraic cycles (read solutions of equations) can form manifolds, if we add more equations then we get algebraic cycles on the manifold.
Adding z = 0 to the equation x+y+z=1, we get a circle
Now from a topological perspective, we can draw crazy shapes on a manifold and then group these shapes together if they can be deformed into each other. They are grouped into homology classes.
Two different homology classes on a torus
Now this looks exactly like the interchange we considered above: we are moving from an algebraic description of a shape and a geometrical description. The problem is, given a manifold, when does a homology class contain one shape that can be described as an algebraic cycle on that manifold?
Now unfortunately, we have been dealing with manifolds that live in regular Euclidean space. The Hodge conjecture deals with manifolds that live in projective complex n-dimensional space (which has real dimension 2n). So here everything hits the fan. A manifold is non-singular if there is no ?pointy bits?.
Hodge came up with a neat and elegant idea to tell if a homology class was equivalent to an algebraic cycle and this is in essence the Hodge conjecture. I will leave it to the interested reader to pursue a post-graduate degree in algebraic geometry if they want to understand more.
And there we go! If you made it this far, well done ? give yourself a pat on the back.
The interested reader can have a peruse through The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles Of Our Time by Keith Devlin. He gives a very good description of each of the problems.
The very interested reader can try to solve one! I dare you.
Photo by ThisisEngineering RAEng on Unsplash
