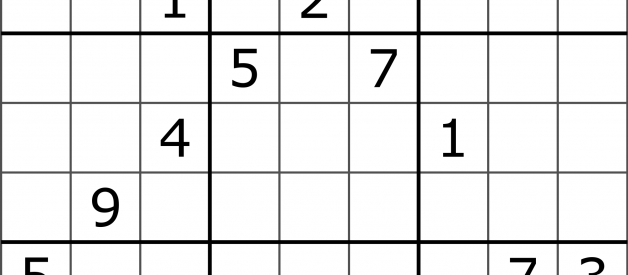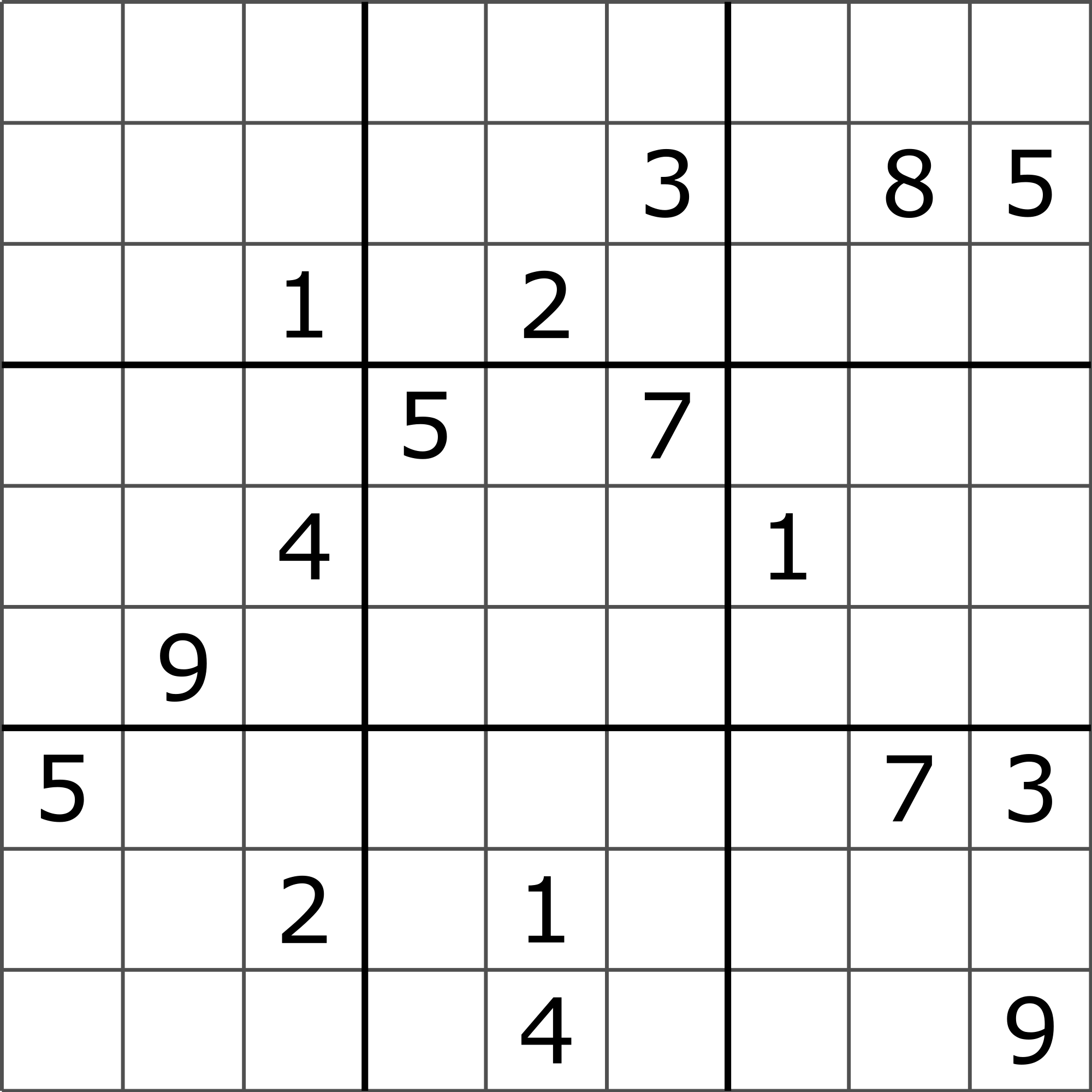
Today, we?re going to learn how to code a Sudoku puzzle solving algorithm in C++! It?s also easy enough to extend to any other program language, so feel free to stick around if Python, Java, or something else is more of your forte!
The word Sudoku is Japanese and is composed of two parts: Su- meaning ?number?, and Doku- meaning ?single?. Rightfully so, as Sudoku is a puzzle where the objective is to fill a 99 square grid with digits numbered 1 to 9, so that each column, each row, and each of the nine 33 sub-grids contains all of the digits, but absolutely NO duplicates. The puzzle starts out partially filled in i.e some of the numbers are given to you as a starting point as shown for example above. It?s quite the mentally stimulating game and is often featured in newspapers, right beside the crossword.
As with any puzzle game, we want to know the absolute best way to play so we can win every time! With Sudoku, there can sometimes be some really tough puzzles that don?t give you many starting numbers, forcing you to think far ahead before filling in any of the grid cells. This is where computers can really come in handy, since computers can perform many logical operations very, very fast. This is exactly what we want when we?re trying to think ahead with many different combinations of numbers.
Enter Brute Force Search (BFS). BFS is one of the most general and basic techniques for searching for possible solutions to a problem. The idea is that we want to generate every possible move within the game and then test to see whether it solves our problem. The step-by-step process is the following:
- Generate a possible move that follows the rules of the game and has not been tested yet.
- Test to see if that move wins the game/is a solution.
- If the move wins the game, exit since you have found your solution! If the move does not win the game, add it to the list of attempted moves so you don?t attempt it again.
Well that seems straight forward enough! Thus with Sudoku, the BFS algorithm visits the empty cells in some order, filling in digits sequentially (from 1 to 9). The program would solve a puzzle by placing the digit ?1? in the first cell and checking if it is allowed to be there. If there are no violations (checking row, column, and box constraints) then the algorithm advances to the next cell, and places a ?1? in that cell. When checking for violations, if it is discovered that the ?1? is not allowed, the value is advanced to ?2?.
HOLD ON; what if a cell is discovered where none of the 9 digits is allowed?! ? Well, then there?s a quick and easy solution to this call Backtracking. If we found a cell where no possible solution exists, then obviously we must have done something wrong with the previous cell. We should go back and change something in one of the previous cells and see if that works. Thus the algorithm will leave this unsolvable cell blank for now and move back i.e backtrack to the previous cell. The value in that cell is then incremented by one. This is repeated until the allowed value in the last (81st) cell is discovered. Backtracking is a depth-first search (in contrast to a breadth-first search), because it will completely explore one branch to a possible solution before moving to another branch. Check out the fun GIF below for an illustration:
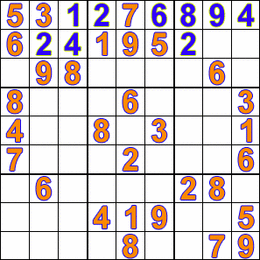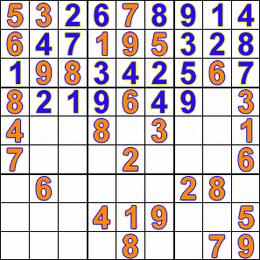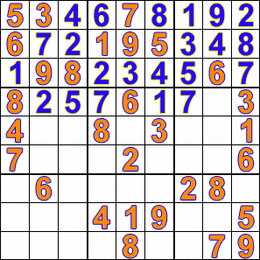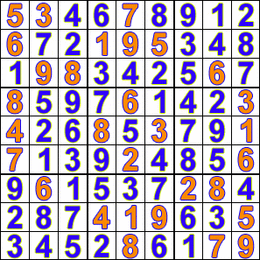
Now everyone’s favorite part?.. Lets code it and see our algorithm in action! We?ll do this in C++.
The first thing to do when programming any game solving algorithm is to define the game itself. First off, we?ll set up the Sudoku grid and a basic function to print it out. We need basic global variables to define the actual grid and how it will be printed. We do this in the code snippet below. Naturally, we define the Sudoku grid as a 2D array of integer type that has size 9×9. Also note that we define BLANK cells with the integer value 0. Thus when we create our initial Sudoku grid, the cells that start out as blank in the grid will be filled with 0s.
Next off we want to define the rules of the game. The computer needs to know to play by the rules just like we do if we want it to solve the puzzle properly. It should know which moves are allowed and which are not, as well as what constitutes as a win! The code below helps us define to the computer which moves are allow and which are not. The first three functions check to see if a given number is already being used in a particular row, column, or box. The ?get_unassigned_location? function is the one the loops through the grid to fill in each cell one-by-one; it is the mover of the BFS algorithm. The ?is_safe? function checks to see if placing a given number in a particular cell is legal i.e it doesn?t violate the rules of the game that are defined by the first three functions.
Finally, we can get to the meat of the code. The function below is the BFS algorithm with backtracking and is responsible for solving the Sudoku puzzle perfectly. As can be seen below, the function is recursive; each time it is called, it is handling a single cell at a time; whichever one has not been assigned yet. For that particular cell, we loop through all possible digits from 1 to 9 and try them out. If a digit is valid for that cell, we move on to the next unassigned cell. If we find that for a particular cell that there are no valid digits, then we return false, then backtrack, incriminating the digit in the previous cell and trying again. If we are able to assign a valid number to every cell in the grid i.e the array is totally full, then the recursive algorithm will return true, jumping out of all the recursive loops having filled in the whole grid with valid numbers.
https://gist.github.com/GeorgeSeif/b67f75a039377a29df70a8f1a26c6f8f
Awesome! We?re all done! All we have to do is define the initial Sudoku grid, pass to our solver function like below, and BAM we?re done and have solved Sudoku!
If you would like to see the full code, check out my GitHub repository. https://github.com/GeorgeSeif/Sudoku-Solver. Any feedback is very much appreciated! Follow me if you learned something new today!