Refer to the note in Pre Linear algebra about understanding Dot product.
Assume that the vector w projects onto the vector v.Notation:
- Scalar projection: Component?w, read as “Component of w onto v”.
- Vector projection: Projection?w, read as “Projection of w onto v”.
Notice that: When you read it, it?s in a reverse order! Very important!
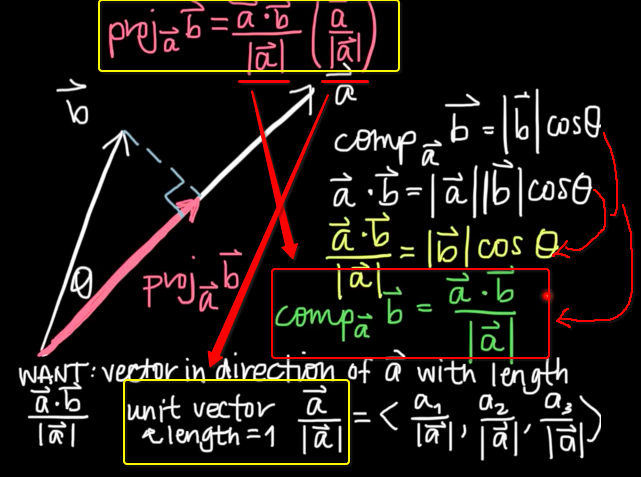
Projection Formula
Note that, the formula concerns of these concepts as prerequisites:
- Dot product calculation
- Dot product cosine formula
- Unit vector
How to calculate the Scalar Projection
The name is just the same with the names mentioned above: boosting.
Component?w = (dot product of v & w) / (w’s length)
Refer to lecture by Imperial College London: ProjectionRefer also to Khan academy: Intro to Projections
What if we know the vectors, and we want to know how much is the Scalar projection(the shadow)?Example:
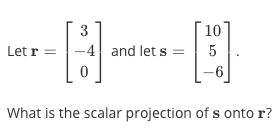
How we?re gonna solve this is: We know the vectors, so we can get their dot producteasily by taking their linear combination; and we know the length of each vector, by using Pythagorean theorem; and then we get the projection, as in the picture.
How to calculate the Vector Projection
It?s another idea for projection, and less intuitive.
Remember that a Scalar projection is the vector’s LENGTH projected on another vector. And when we add the DIRECTION onto the LENGTH, it became a vector, which lies on another vector. Then it makes it a Vector projection.
It can be understood as this formula:
Projection?w = (Component?w) * (Unit vector of v)
But usually we write it as this:
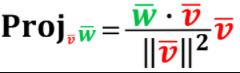

Refer also to video for formula by Kate Penner: Vector Projection EquationsRefer to video by Firefly Lectures: Vector Projections ? Example 1
Example:
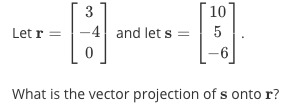
–


