*ROOT* LEFT RIGHT

Types of Binary Tree traversal and its Conversion of inorder to preorder-postorder

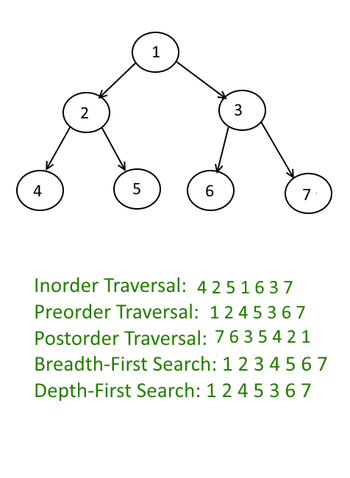
Binary Tree Traversals

Motivation:

• Pre-order traversal while duplicating nodes and values can make a complete duplicate of a binary tree. It can also be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly.
• In-order traversal is very commonly used in binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name).
• Post-order traversal while deleting or freeing nodes and values can delete or free an entire binary tree. It can also generate a postfix representation of a binary tree

we are using stack 🙂 So here we go!

Inorder Traversal :

LEFT *ROOT* RIGHT

Since we are not using recursion, we will use the Stack to store the traversal, we need to remember that inorder traversal is, first traverse the left node then root followed by the right node.

Psuedo code:

1. Create a Stack
2. Push the Root onto Stack until set the root = root.left continue till it hits the NULL.
3. If root is null and Stack is empty Then return, we are done.
4. Else Pop the top Node from the Stack and set it as, root = popped_Node.
5. print the root and go right, root = root.right.
6. Go to step. End If

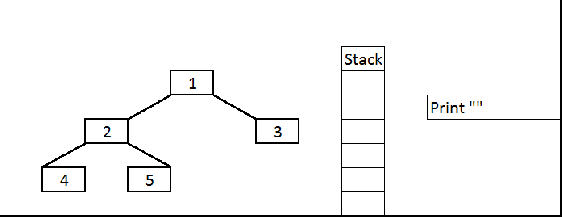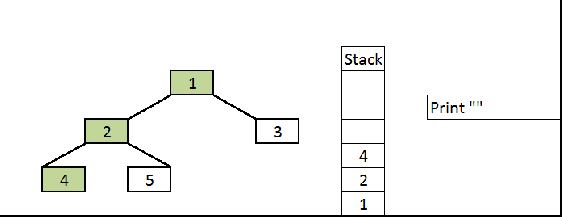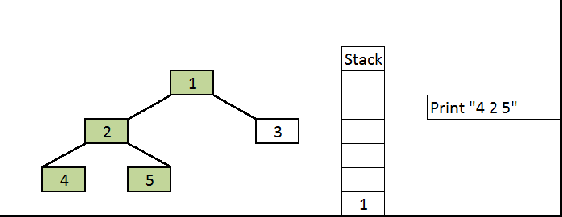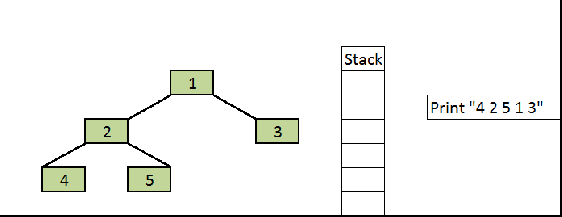working Inorder Stack

we have to keep track of the root that?s why we use stack! if we consider each subtree as separate ones it gets easier to understand the traversal and then move to stack

Inorder Traversal using stack

Output: inorder

4 2 5 1 34 2 5 1 3

Preorder Traversal: we need to remember that preorder traversal is, the first traverse the root node then left node followed by the right node.

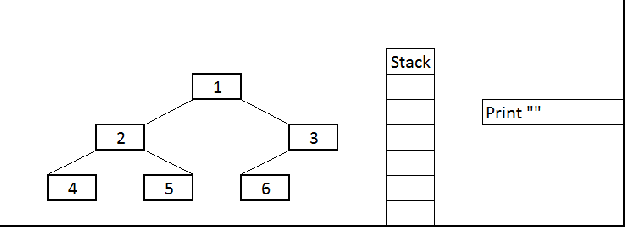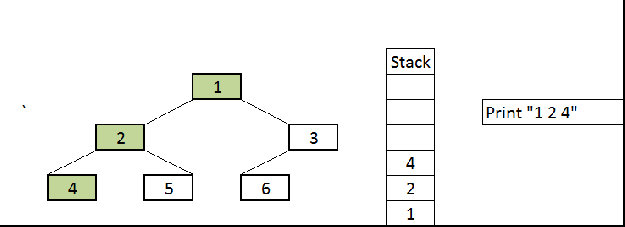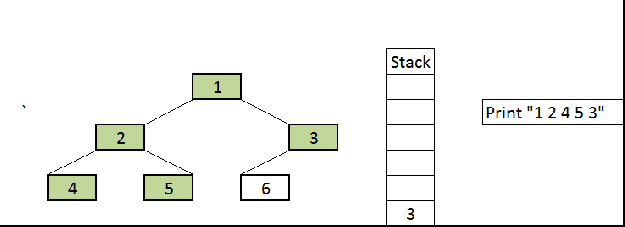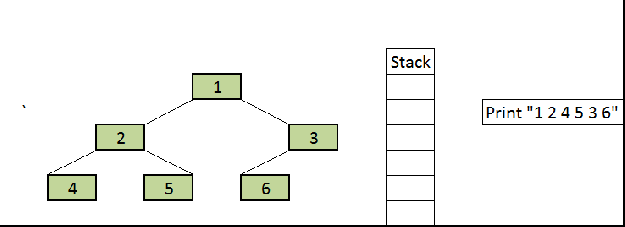Preorder Traversal

Output:

1 2 4 5 3 6 71 2 4 5 3 6 7

Postorder Traversal: we need to remember that preorder traversal is, the first traverse the root node then left node followed by the right node.

LEFT RIGHT *ROOT*

Approach:

• We have seen how we do inorder and preorder traversals without recursion using Stack, But post order traversal will be different and slightly more complex than other two. Reason is post order is non-tail recursive ( The statements execute after the recursive call).
• If you just observe here, postorder traversal is just reverse of preorder traversal (1 3 7 6 2 5 4 if we traverse the right node first and then left node.)
• So idea is follow the same technique as preorder traversal and instead of printing it push it to the another Stack so that they will come out in reverse order (LIFO).
• At the end just pop all the items from the second Stack and print it.

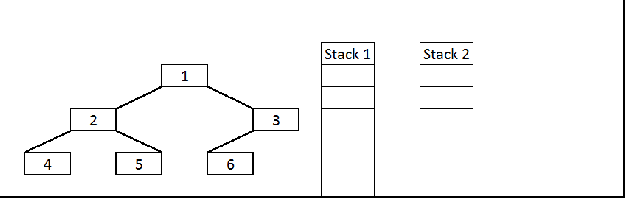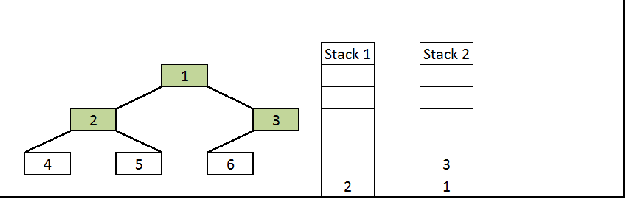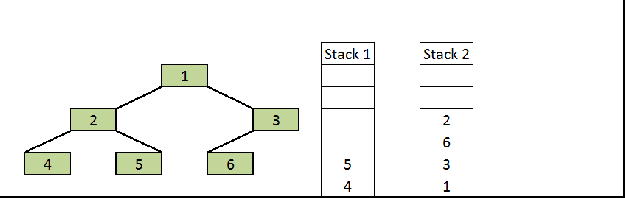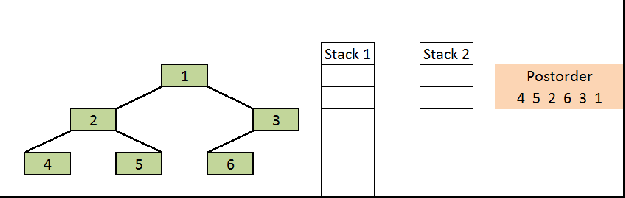PostOrder Stackpreorder stack

Output:

4 5 2 6 7 3 14 5 2 6 7 3 1

Resources: https://en.wikipedia.org/wiki/Tree_traversal

find more and more knowledgeable resources related to #ai #machinelearning #deeplearning #python?https://twitter.com/Ajinkya_Tweets

Ajinkya Jawale, https://www.linkedin.com/in/ajinkya-jawale-b3421a12a/

https://angel.co/ajinkya-jawale

reach me here, [email protected]

gracies!