Part One: Solving Triangles w/ Sine, Cosine, & Tangent
You might be surprised to find that the heart of Trigonometry lies in Geometry. Understanding the relationships used to solve right triangles geometrically is fundamental to pretty much everything you do Trigonometry. So whether you?re learning this for the first time or are here for a little refresher you?ll walk away from today?s tutorial with a good grasp at how to solve right triangles.
Click to SUBSCRIBE on YT 🙂
Three Key Concepts
We?ll be using three key concepts in today?s lesson:
- Trig Functions: Sine, Cosine, and Tangent (aka SOH CAH TOA)
- The Pythagorean Theorem: a + b = c
- 180 degrees in a triangle
That?s it! Master those three things and you?ve learned how to solve the majority of right triangles. (For the final scenarios, you can check out part two of this series!)
But first, a Few Questions You Might Have?
What does ?Solving a Triangle? Mean?
Before we jump into solving some problems. Let?s recap some pertinent information. First of all, what do we mean by ?solving a right triangle??
Solving the triangle simply means that we want to find values for all of the missing parts. This includes any missing side lengths and angle measures.
How Do You Know You Have a Right Triangle?
First of all, everything we do today only works when you have a right triangle. How do you know you have a right triangle? Look for a little square drawn in one of the angles of the triangle. That square indicates the angle is a 90-degree angle, and therefore you have a right triangle.
Is There Any Special Triangle Notation?
Yes. Often the angles will be labeled with capital letters such as A, B, and C. The side lengths will be labeled with lower case letters: a, b, and c. The sides and angles will be arranged so that the angle measure is across from the corresponding side length. For example, angle A would be across from side a, angle B opposite leg b, and angle C across from leg c.
When using the Pythagorean Theorem, c is always the hypotenuse. And remember the hypotenuse is always the leg across from the 90-degree right angle, and it is also always the longest leg.
Example: Solve the Following Triangle
*To see this example, plus a bonus example, worked out live check out my video tutorial above*
We?re going to start off by jumping straight into an example and I?ll explain things as we go. Let?s solve this right triangle where we are given a 23-degree angle and know that the leg adjacent to the 23-degree angle is 4.5 units long.
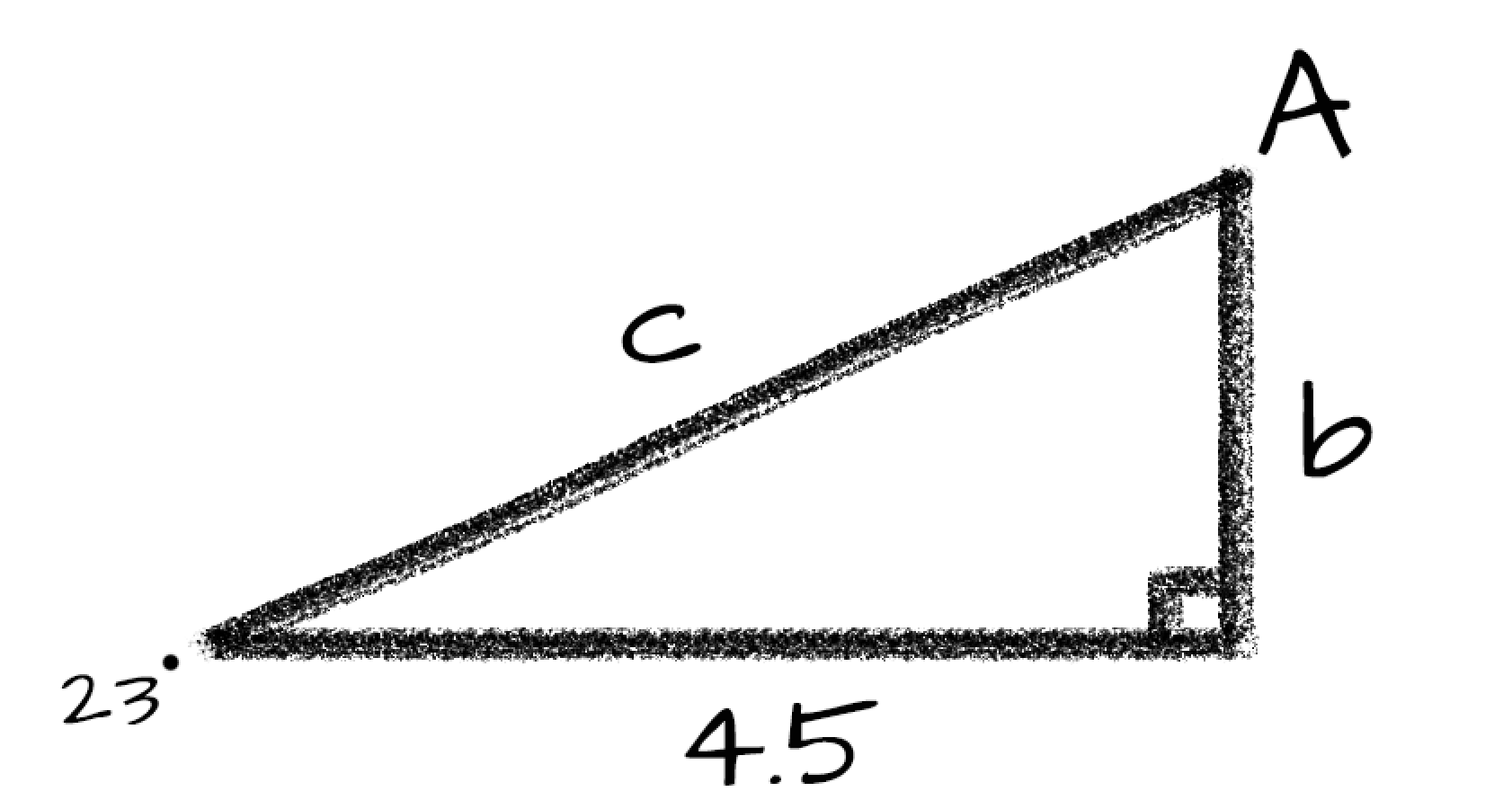
To solve the triangle we?ll need to find the length of the other leg and the hypotenuse as well as the measure of the remaining angle.
Solve for Leg b
You can start solving in whatever order you like. I?m going to start by solving for the side length of leg b. To solve for b, we need to use one of our three trig functions: Sine, Cosine, and Tangent. Each of these functions takes an angle as its input and is equivalent to the ratio of two specific side lengths of a right triangle.
As we walk through the different relationships Sine, Cosine and Tangent are equal to remember to keep in mind that you must always work from the perspective of the angle you are inputting into the function. You?ll see what I mean as we walk through the next part.
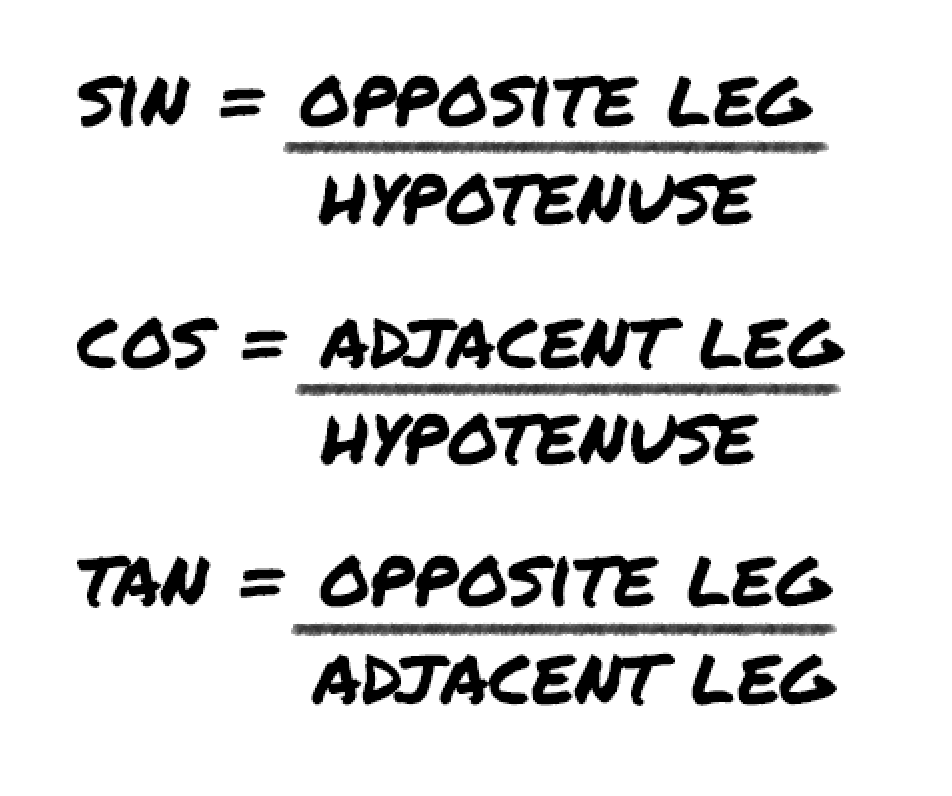
SOH CAH TOA Explained
You?ve probably heard of the mnemonic SOH CAH TOA. It?s the most popular way to remember the relationship of the trig functions Sine (abbreviated as Sin), Cosine (abbreviated as Cos) and Tangent (abbreviated as Tan).
- SOH stands for Sin(x) = Opposite leg / Hypotenuse
- CAH stands for Cos(x) = Adjacent leg / Hypotenuse
- TOA stands for Tan(x) = Opposite leg / Adjacent leg
Where x represents the measure of the angle you are working from.
In this problem, we are working from the perspective of the 23-degree angle. To determine which trig function you want to use to solve for the missing leg b, imagine you are standing at the 23-degree angle. From that position side b is directly opposite you on the far side of the triangle. Therefore you know that the function you want to use must include the ?opposite leg?. So we?ll be using either Sine or Tangent.
Next, you want to use the side length that you were given (if you weren?t given any side lengths then you can?t solve the triangle without more information). In this problem, that means that you want to use the 4.5 unit leg. That leg is next to you so refer to it as the adjacent leg. Therefore we?ll use the Tangent function since TOA stands for Tan(x) = Opposite leg / Adjacent leg.
- It?s important to note here that the hypotenuse (the leg across from the 90-degree angle) is never referred to as anything but the hypotenuse. You don?t want to accidentally misidentify it as the adjacent or opposite leg. No matter what angle you?re working from it?s always called the hypotenuse.
Now that you?ve determined which function you want to use, it?s time to set up the equation. Start by writing down Tangent with 23 degrees as it?s input.
Then set it equal to the opposite leg divided by the adjacent leg. The opposite leg is b, which we are solving for. The adjacent leg has a length of 4.5, so go ahead and write down 4.5 in its place.
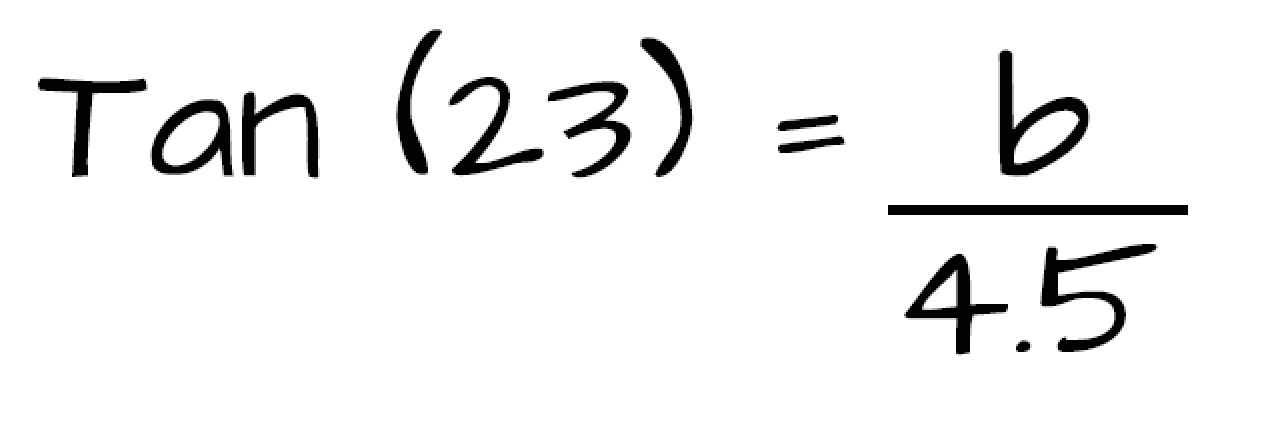
Next, let?s evaluate the Tan(23) using a calculator. Before you punch it in make sure you are in degree mode (not radians). Then multiply both sides by 4.5 to isolate b. Therefore b has a length of approximately 1.91 units.
Solve for c, the Hypotenuse
Next, we can solve for c, the hypotenuse. Because we now know the lengths of sides of a right triangle you have two options for solving for c: you can use one of the SOH CAH TOA trig functions or you can use the Pythagorean Theorem. Which you choose may depend on the instruction in your assignment or maybe just your preference.
Solving Using Cosine
If you choose to solve for the hypotenuse using the trig functions, you?ll first need to determine which function to use. Again you are standing at the 23-degree angle, but this time you want to solve for the hypotenuse. So you?ll be using either Sine (SOH) or Cosine (CAH) since both include the hypotenuse in their ratios.
Next, you want to include the side length you know. At this point, you know both the opposite and the adjacent legs? lengths. I?d recommend using the 4.5 unit adjacent leg. That way if you made an error in calculating the opposite leg, you won?t cause this problem to be incorrect as well.
So we have the hypotenuse and the adjacent leg, which means we?ll be using Cosine. Go ahead and set up your equation using 23 as the input degree measure.
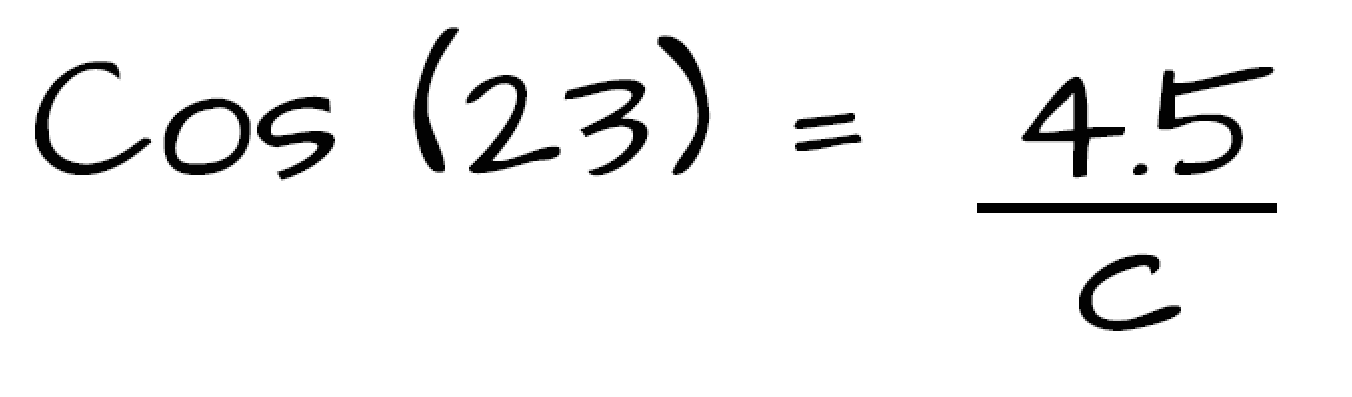
The algebra is a little trickier with this one. I?d recommend using cross multiplication to help isolate c.
Alternate Method: Pythagorean Theorem
It?s really simple to solve for the hypotenuse using the Pythagorean Theorem when you already know the lengths of the two legs. The Pythagorean Theorem states that the sum of the squares of the two legs is equal to the square of the hypotenuse. So simply fill in the side lengths for a and b and solve for c.
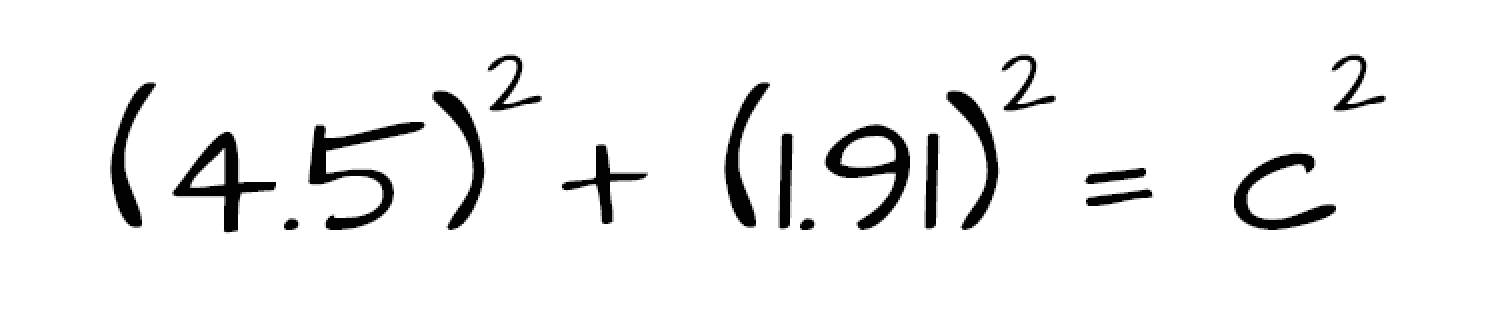
Find the Measure of Angle A
Our last task is to solve for the missing angle A. Since we already know the degree measure of the two other angles in the triangle we can use the fact that the angles of a triangle always sum to 180 degrees to create an equation to solve for the missing angle.
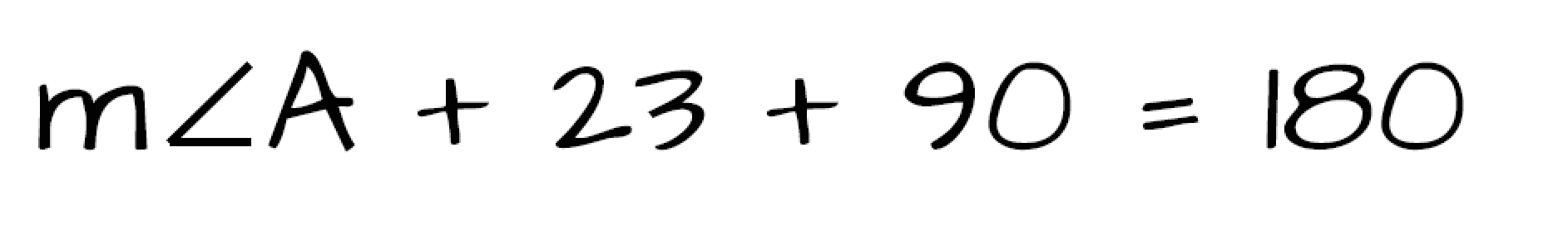
Therefore the measure of Angle A is 67 degrees.
In part two of this series, we?ll learn about the inverse trig functions of Sine, Cosine, and Tangent and how to use them to solve for missing angles.
Need More Math Help?
- Check out Math Hacks on YouTube for more hands-on math tutorials covering popular topics from Algebra through College Math.
- You can find a number of interesting math topics and problems right here on Medium, just click that follow button!
Thanks for joining me!
? Brett


