Random variables and the various distribution functions which form the foundations of Machine Learning
Table of contents
- Introduction
- Random Variable and its types
- PDF (probability density function)
- PMF (Probability Mass function)
- CDF (Cumulative distribution function)
- Example
- Further Reading
Introduction
PDF and CDF are commonly used techniques in the Exploratory data analysis to finding the probabilistic relation between the variables.
Before going through the contents in this page ,first go through the fundamental concepts like random variable, pmf, pdf and cdf.
Random variable
A random variable is a variable whose value is unknown to the function i.e, the value is depends upon the outcome of experiment
For example, while throwing a dice, the variable value is depends upon the outcome.
Mostly random variables are used for regression analysis to determine statistical relationship between each other. There are 2 types of random variable:
1 ? Continuous random variable
2 ? Discrete random variable
Continuous random variable:- A variable which having the values between the range/interval and take infinite number of possible ways is called Continuous random variable . OR the variables whose values are obtained by measuring is called Continuous random variable. For e.g, A average height of 100 peoples, measurement of rainfall
Discrete Random Variable:-A variable which takes countable number of distinct values. OR the variables whose values are obtained by counting is called Discrete Random Variable. For e.g, number of students present in class
PDF (Probability Density Function):-
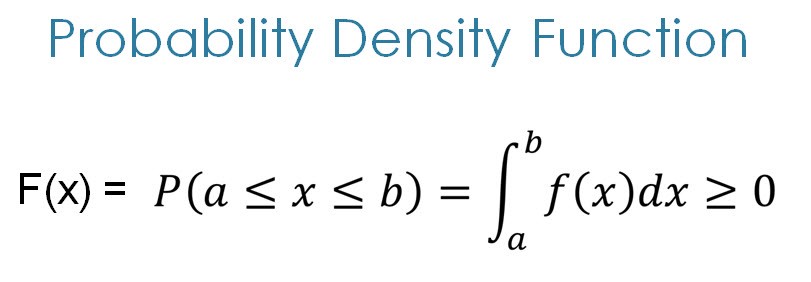 The formula for PDF
The formula for PDF
PDF is a statistical term that describes the probability distribution of the continues random variable
PDF most commonly follows the Gaussian Distribution. If the features / random variables are Gaussian distributed then PDF also follows Gaussian Distribution. On PDF graph the probability of single outcome is always zero, this happened because the single point represents the line which doesn?t cover the area under the curve.
PMF (Probability Mass Function):-
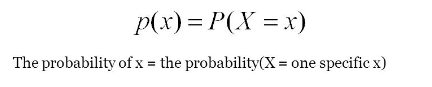 Fig:- Formula for PMF
Fig:- Formula for PMF
PMF is a statistical term that describes the probability distribution of the Discrete random variable
People often get confused between PDF and PMF. The PDF is applicable for continues random variable while PMF is applicable for discrete random variable For e.g, Throwing a dice (You can only select 1 to 6 numbers (countable) )
CDF (Cumulative Distribution Function):-
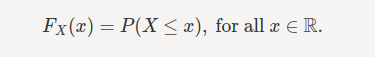 Fig:- Formula for CDF
Fig:- Formula for CDF
PMF is a way to describe distribution but its only applicable for discrete random variables and not for continuous random variables. The cumulative distribution function is applicable for describing the distribution of random variables either it is continuous or discrete
For example, if X is the height of a person selected at random then F(x) is the chance that the person will be shorter than x. If F(180 cm)=0.8. then there is an 80% chance that a person selected at random will be shorter than 180 cm (equivalently, a 20% chance that they will be taller than 180cm)
Python example for PDF and CDF on Iris Dataset:-
The iris data set contains the following data:-
 Fig:- Flower image from iris dataset
Fig:- Flower image from iris dataset
The detailed explanation of iris data-set is here
PDF On Iris:-
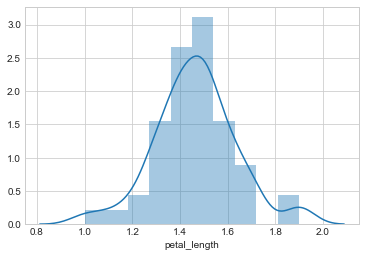 PDF for [?species?]== ?setosa? on petal length
PDF for [?species?]== ?setosa? on petal length
CDF on Iris:-
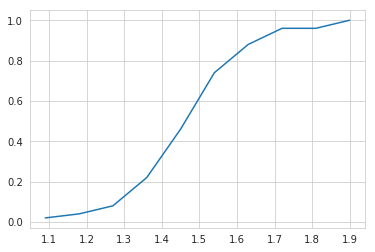 CDf of iris_setosa using petal length
CDf of iris_setosa using petal length
Both PDF and CDF visualisation:-
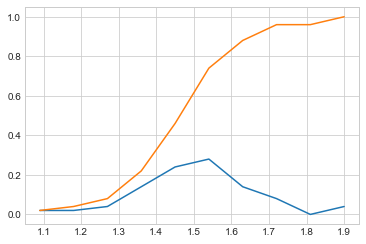 Pdf and Cdf
Pdf and Cdf
You will find the detailed explanation with python code on Github Here.

