What are Pathfinding Algorithms?
Pathfinding algorithms are usually an attempt to solve the shortest path problem in graph theory. They try to find the best path given a starting point and ending point based on some predefined criteria.
What is the shortest path problem?
?In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.?
That?s a pretty dense sentence, so let?s try and unpack it. What it is essentially trying to say is ?Find the shortest path in between two points or nodes in a graph.?
What is a graph / graph theory?
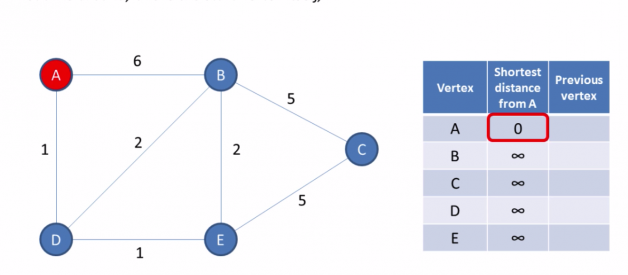
They are mathematical structures used to model pairwise relationships in between objects. A graph consists of nodes/vertices/points that are connected edges/links/lines. I know this may seem a little confusing but just look to the visual below for more clarification.
 Sourced from https://en.wikipedia.org/wiki/Graph_theory
Sourced from https://en.wikipedia.org/wiki/Graph_theory
The circles with letters in them are nodes/vertices/points and the lines connecting/relating the circles are the edges/links/lines. The letters in the circles uniquely represent that circle. The numbers on the lines represent how much it will cost to move along that line.
Why are they important?
Path finding algorithms are important because they are used in applications like google maps, satellite navigation systems, routing packets over the internet. The usage of pathfinding algorithms isn?t just limited to navigation systems. The overarching idea can be applied to other applications as well. The usage will become clearer as we talk about some examples and implementations of pathfinding algorithms.
Examples of Pathfinding Algorithms?
Some examples?
Dijkstra?s AlgorithmA* Search AlgorithmD* Algorithm
Dijkstra?s Algorithm
Steps
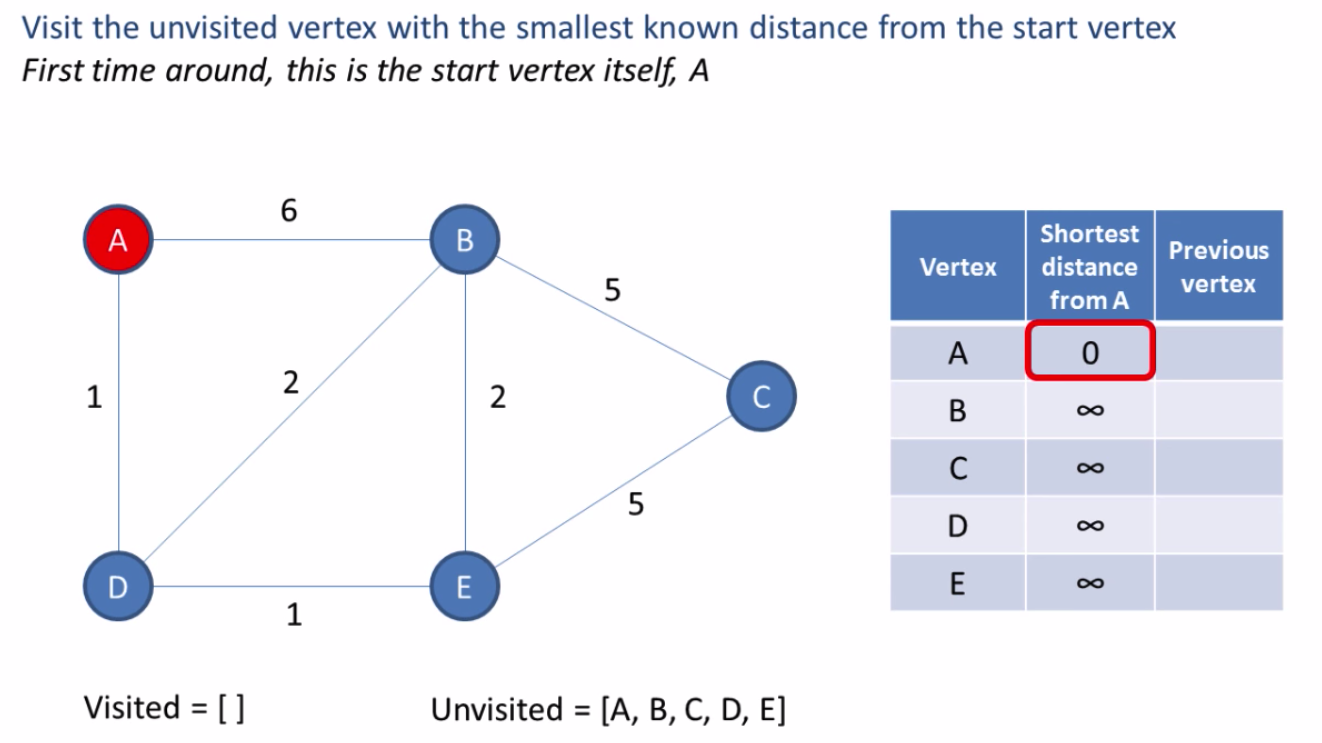
0. The starting node is considered to be solved
- Identify all unsolved nodes that are connected to any solved node
- For each line connecting a solved node to a unsolved node, calculate the candidate cost. A candidate is an unsolved node.
- Choose the candidate with the smallest cost. If there is a tie, then chose one arbitrarily.
- Change the smallest candidate status to solved from unsolved.
- Add the line to the set keeping track of that path.
- Repeat steps 1?5 until we have reached the destination node.
Visualization
If you want to see a visual representation of this process please follow the link below.
Dijkstra’s Algorithm for Shortest Route Problems
Below is a network with the arcs labeled with their lengths. The example will step though Dijkstra’s Algorithm to find?
optlab-server.sce.carleton.ca
 1
1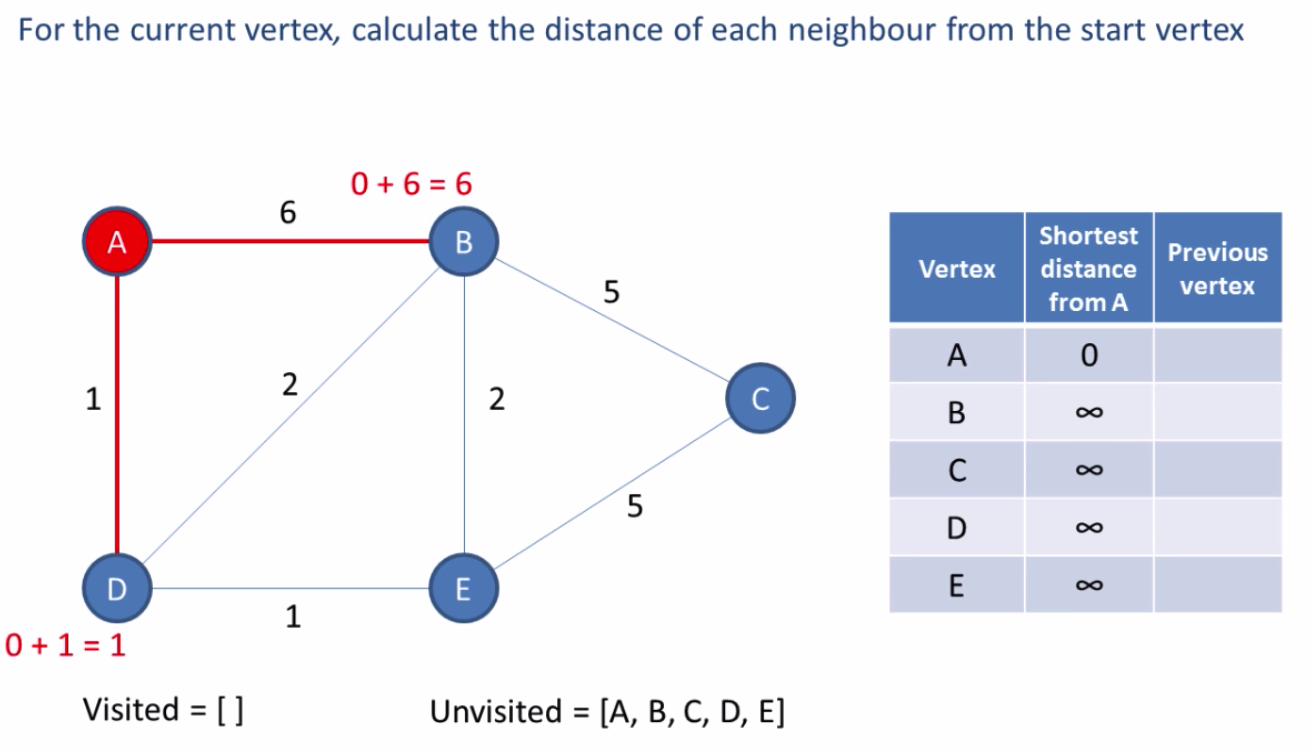 2
2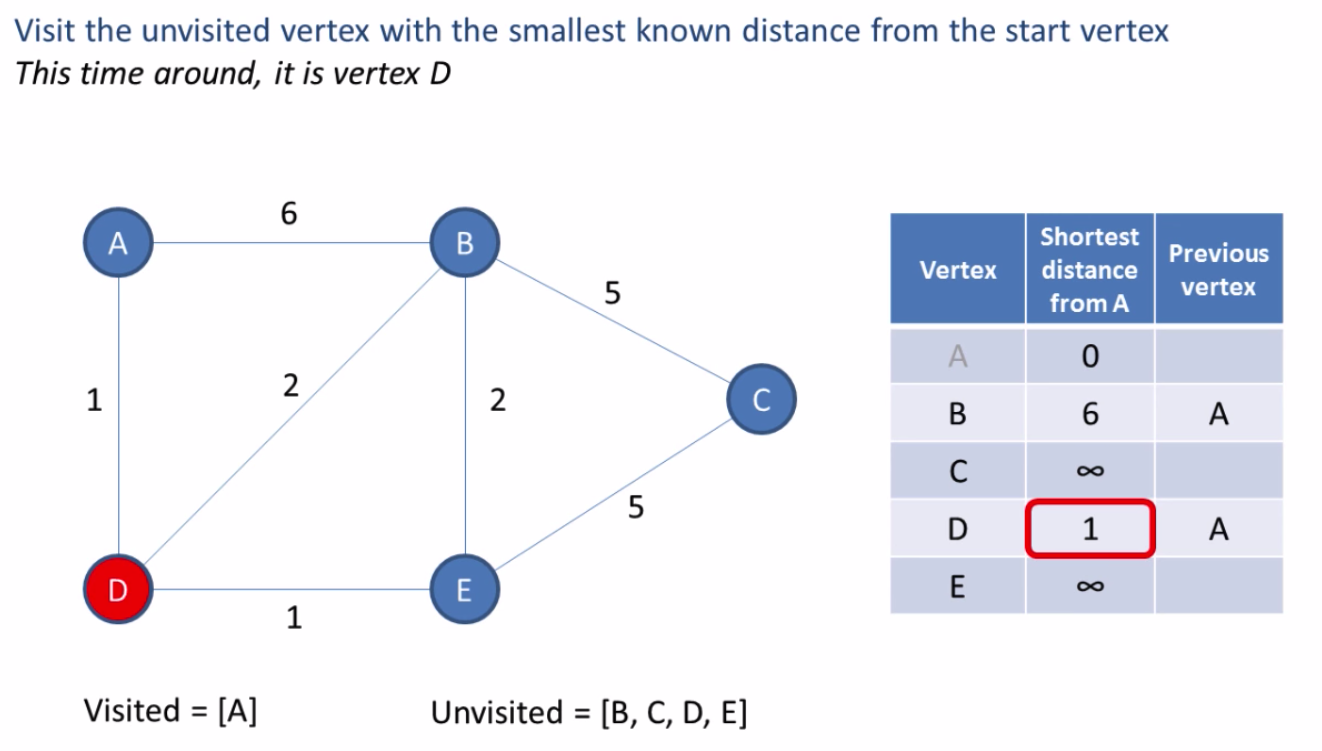 3
3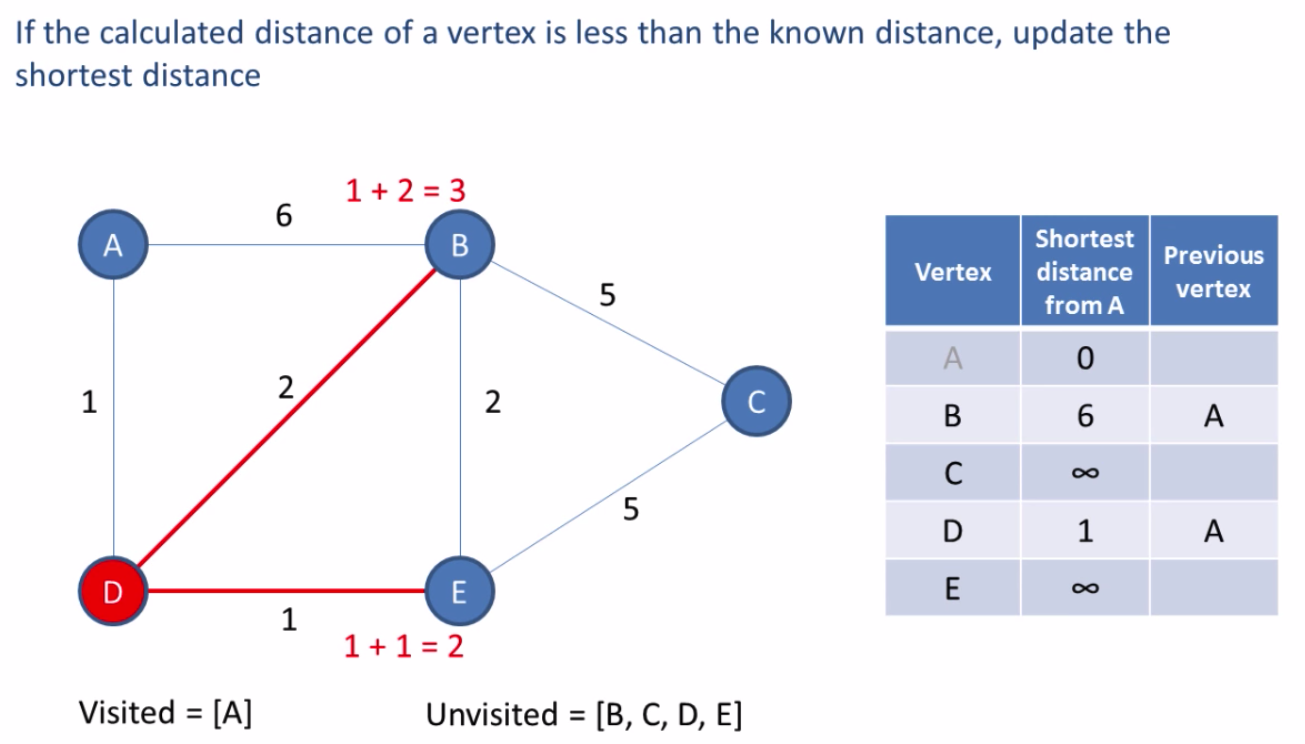 4
4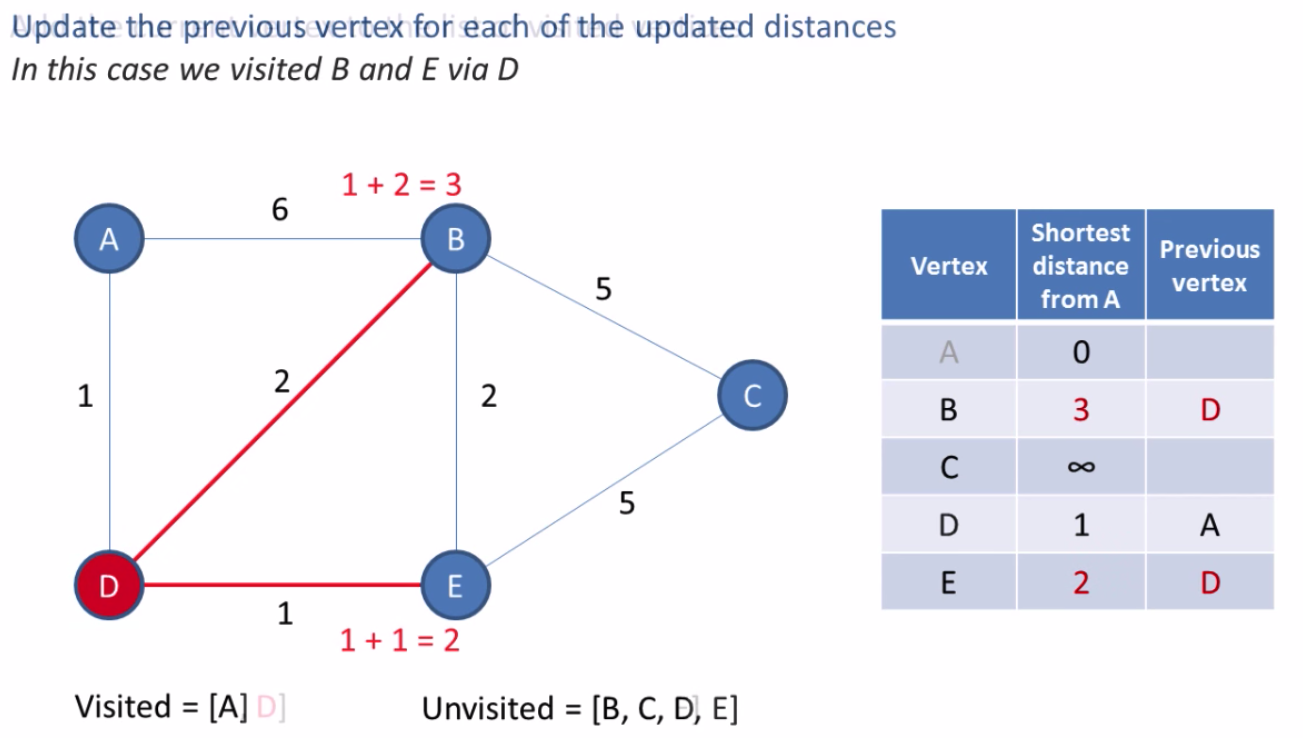 5
5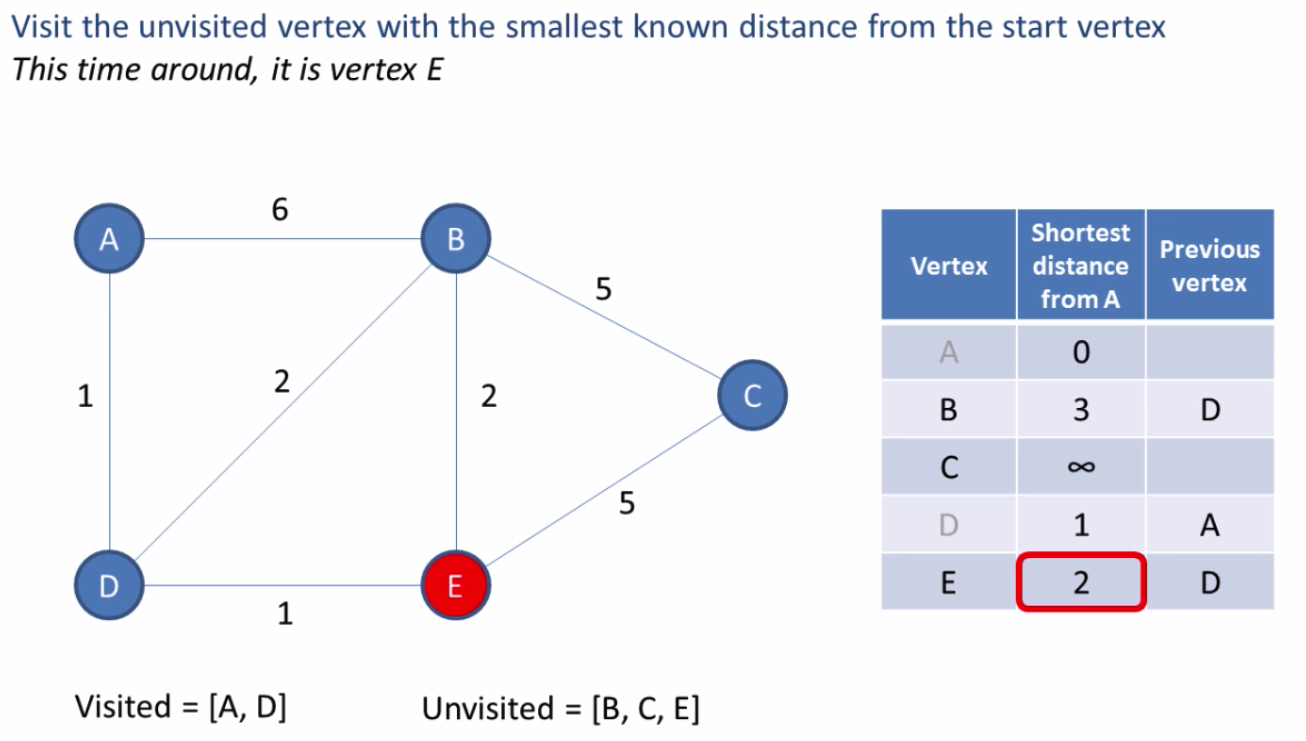 6
6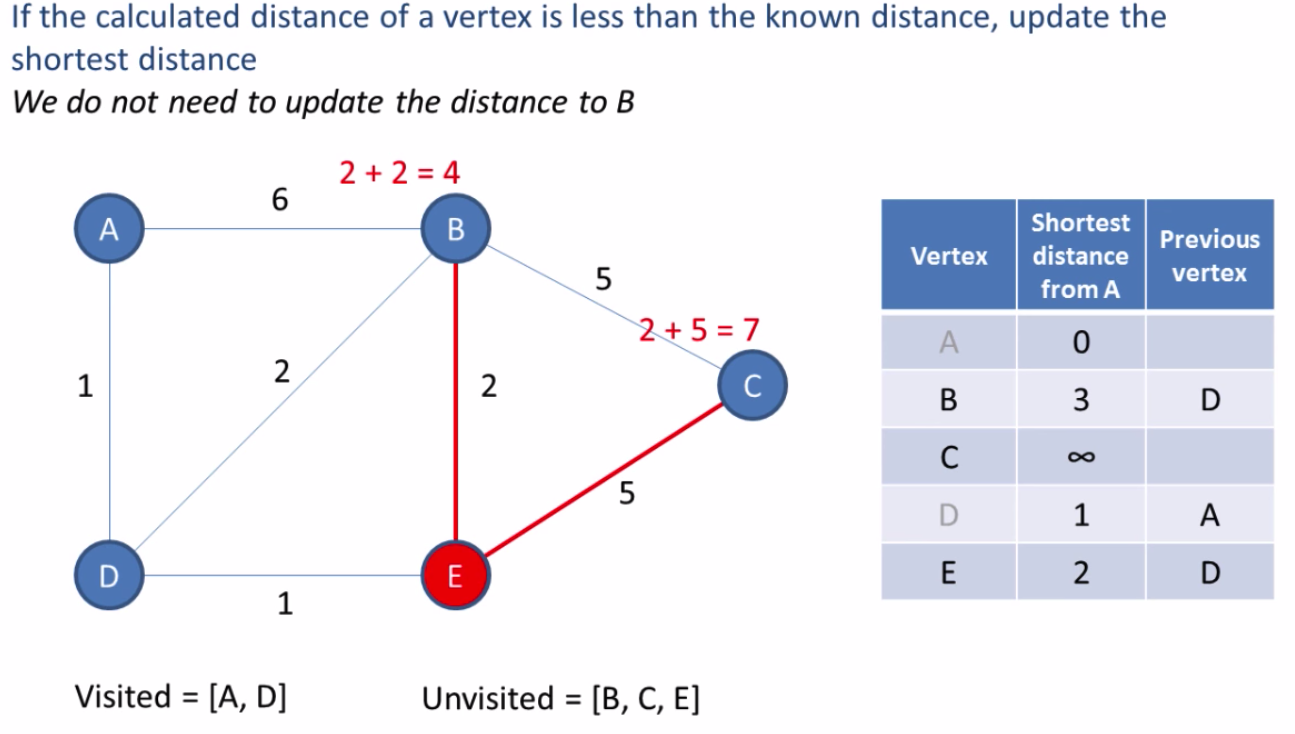 7
7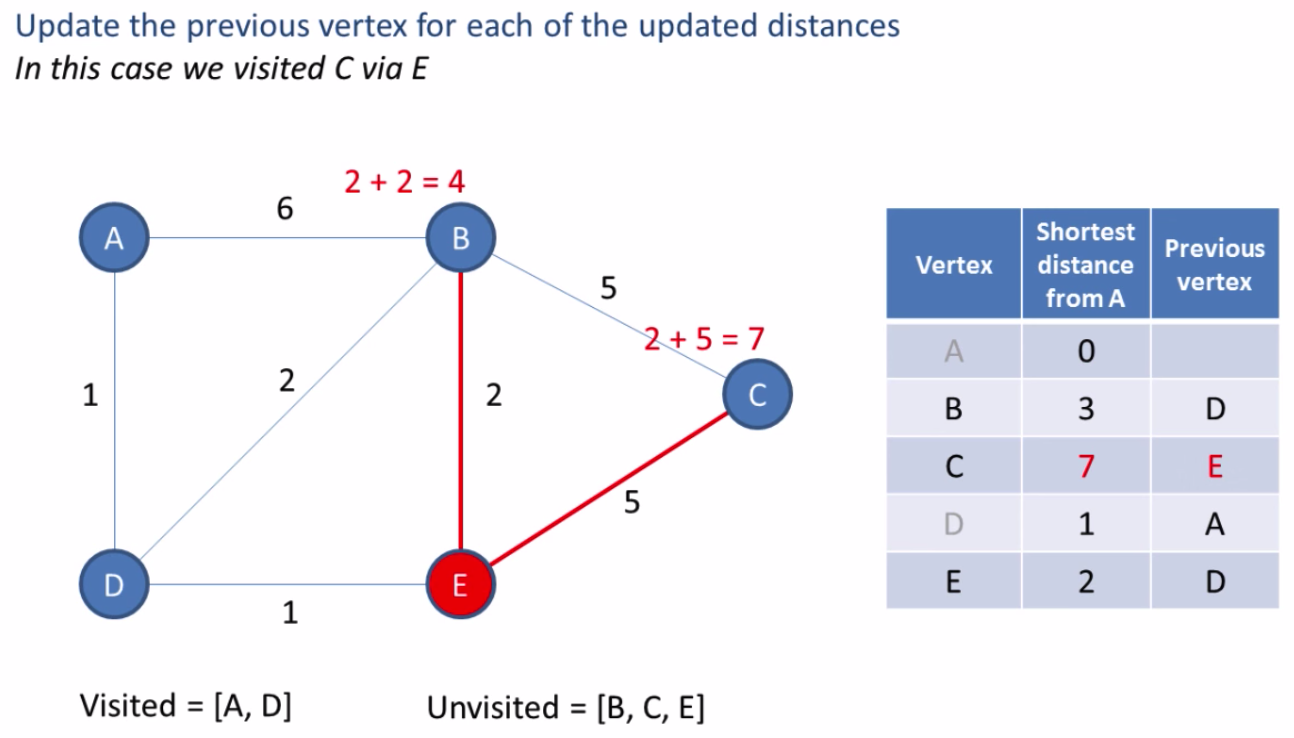 8
8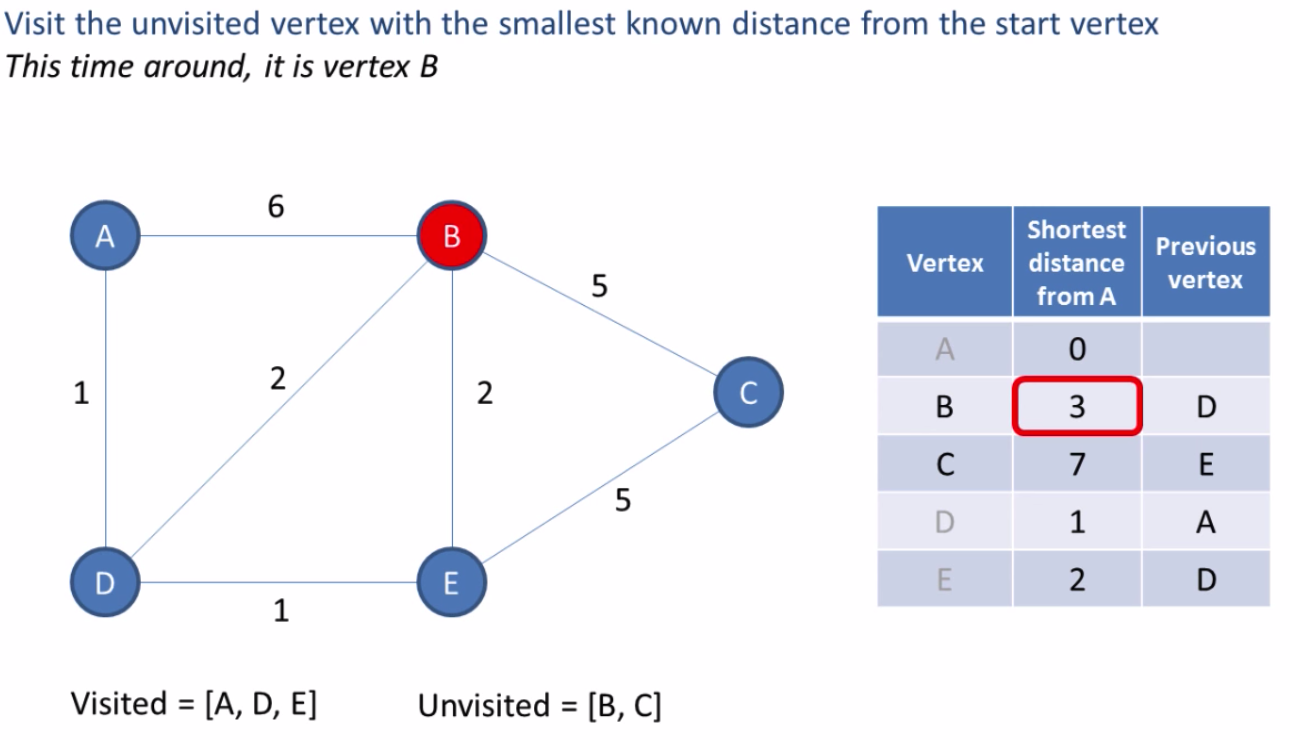 9
9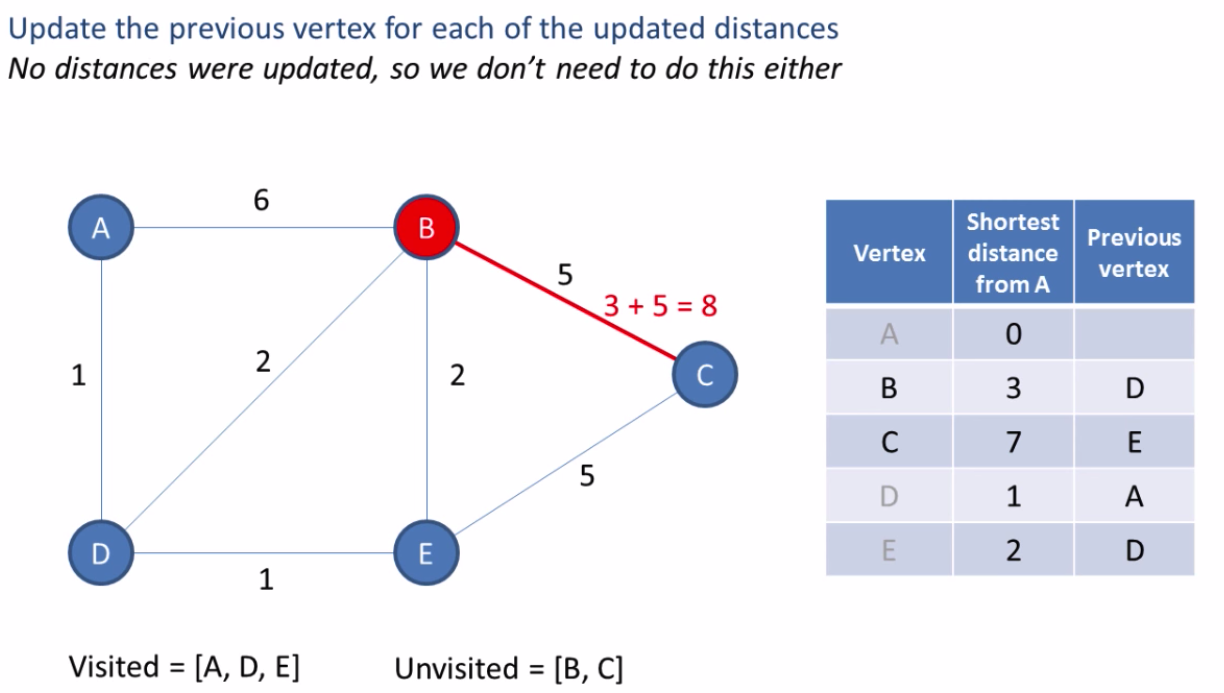 10
10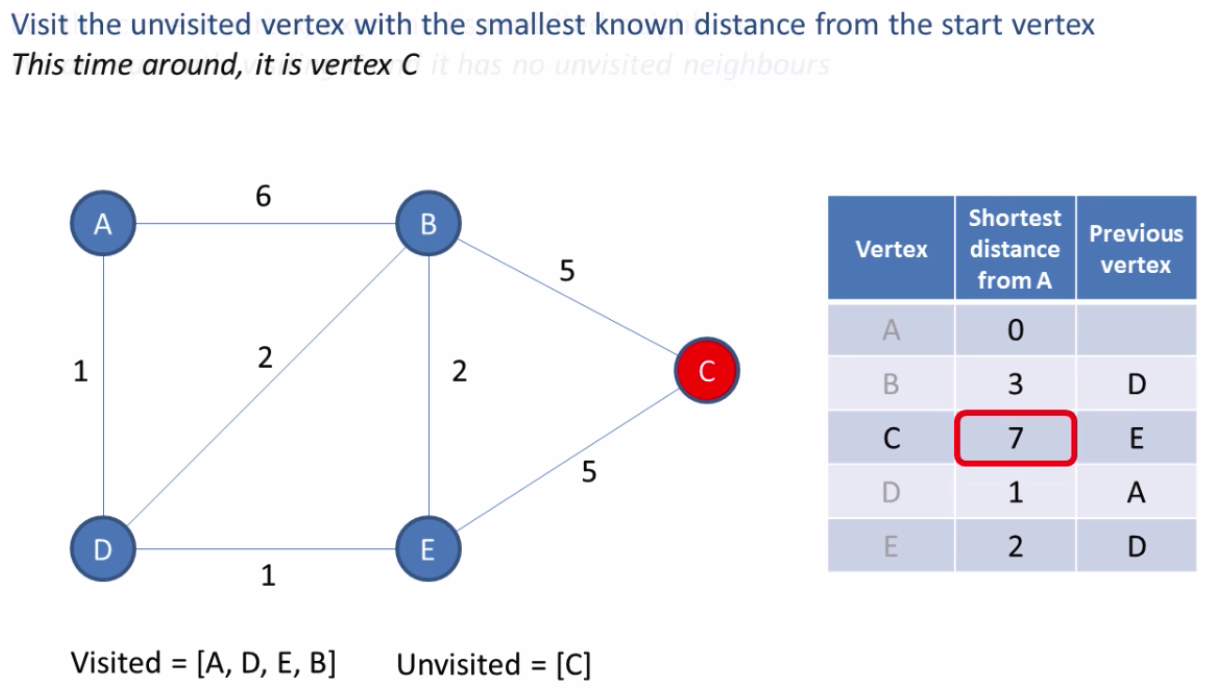 11
11
Images labeled 1?11 were source from Computer Science on Youtube
Based on the table in the last image we can see the shortest path to each node. The shortest path from A to C is A ? D ? E ? C
Resources
Pathfinding – Wikipedia
needs additional citations for verification .improve this article by adding citations to reliable sources. Unsourced?
en.wikipedia.org
Shortest path problem – Wikipedia
The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of?
en.wikipedia.org
https://en.wikipedia.org/wiki/Graph_theory