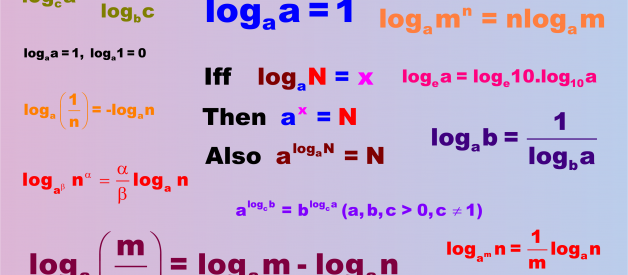Logarithm Rules and Examples
Logarithm Rules
In this article, you will get complete detail and examples of various Logarithm Rules and Exponent Rules and relation between log and exponent.
Logarithm Rules and examples
It is essential to grasp the relation between exponent and log to completely understand logarithms and its rules and apply them on various questions and examples.
We will start with very basic logarithm and exponential rules and stretch it to high-level examples. There is also a Relation between the natural logarithm and common logarithm. Finally, you can also download logarithm rules pdf, examples, and worksheet related to logarithm and exponential rules and pdf.
Logarithm Rules and Logarithm Definition
?The Logarithm of a given number to a given base is the exponent of the power to which the base must be raised in order to equal the given number.?
If a > 0 and a ? 1 then logarithm of a positive number N is defined as the exponent x of that power of ?a? which equals N. These rules are also known as Basic logarithm Rules or Log Rules.
Basic Logarithm Rules To Remember
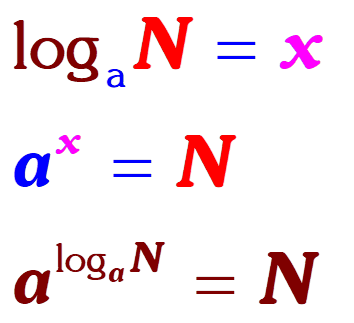Basic Logarithm Rules
Comparison of Exponential Rules and Logarithm Rules
See the following table for the comparison of exponential rules and logarithm rules and memorize it to be comfortable for further logarithm and exponential rules.
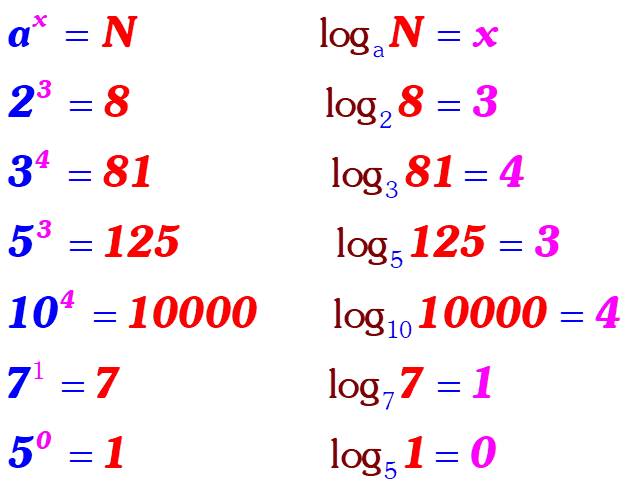Relation between exponents and logarithms
Standard Logarithm Rules
Let m and n be arbitrary positive numbers such that a>0,a?1, b>0, b?1 then
1. Zero Rule
log1=0
The logarithm of 1 to any positive base is zero. Provided base must not be 1.
2. Identity Rule
loga (a) = 1
The logarithm of any positive number ?a? to same base ?a? is one. Provided ?a? must not be 1.
3. Product Rule
log(mn)=logm+logn
Logarithm of product of numbers is equal to the sum of logarithm of individual numbers
4. Quotient Rule
log(m/n)=logm?logn
Logarithm of quotient of two numbers is equal to the difference of logarithm of individual numbers.
5. Power Rule
log(m^n)=n. log(m)
Logarithm of an exponential number is the exponent times the logarithm of the base.
6. Reciprocal Rule
log(1/n)=?log(n)
1/n is equal to n raise to power -1, so by using power rule we get desired result.
