In this article we will understand why do we need regularization, what is regularization, what are different types of regularizations -L1 and L2, what is the difference between L1 and L2 regularization
prerequisites: Machine learning basics, Linear Regression, Bias and variance, Evaluating the performance of a machine learning model
Why do we need regularization?
We want to predict the ACT score of a student. For the prediction we use student?s GPA score. This model fails to predict the ACT score for a range of student?s as the model is too simple and hence has a high bias.
We now start to add more features that may have an influence on student?s ACT score. we add more input features to our model, attendance percentage, average grades of the student in middle school and junior high, BMI of the student, average sleep duration. we see that model has started to get too complex with more input features.
Our model has also learnt data patterns along with the noise in the training data. When a model tries to fit the data pattern as well as noise then the model has a high variance ad will be overfitting.
An overfitted model performs well on training data but fails to generalize.
Goal of our machine learning algorithm is to learn the data patterns and ignore the noise in the data set.
How do we solve the problem of overfitting?
we can solve the problem of overfitting using
- Regularization technique
- Cross Validation
- Drop out
What is Regularization?
Regularization is a technique to discourage the complexity of the model. It does this by penalizing the loss function. This helps to solve the overfitting problem.
Let?s understand how penalizing the loss function helps simplify the model
Loss function is the sum of squared difference between the actual value and the predicted value
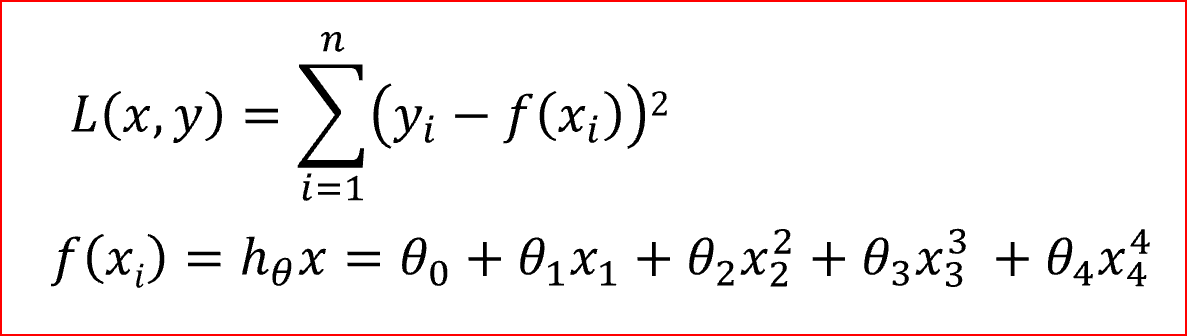Loss function for a linear regression with 4 input variables. In the equation i=4
As the degree of the input features increases the model becomes complex and tries to fit all the data points as shown below
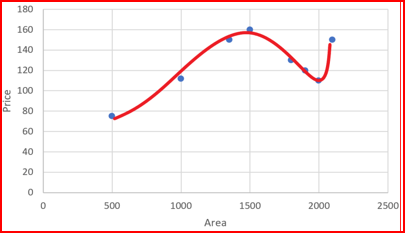
When we penalize the weights ?_3 and ?_4 and make them too small, very close to zero. It makes those terms negligible and helps simplify the model.
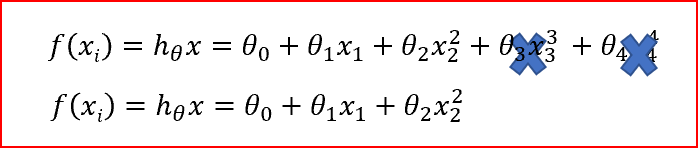
Regularization works on assumption that smaller weights generate simpler model and thus helps avoid overfitting.
What if the input variables have an impact on the output?
To ensure we take into account the input variables, we penalize all the weights by making them small. This also makes the model simpler and less prone to overfitting
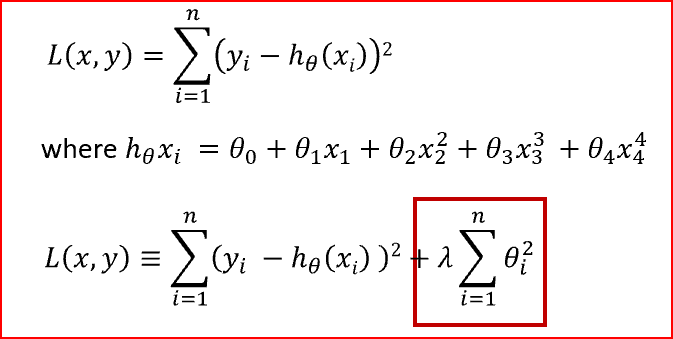Loss function with regularization term highlighted in red box
We have added the regularization term to the sum of squared differences between the actual value and predicted value. Regularization term keeps the weights small making the model simpler and avoiding overfitting.
? is the penalty term or regularization parameter which determines how much to penalizes the weights.
When ? is zero then the regularization term becomes zero. We are back to the original Loss function.
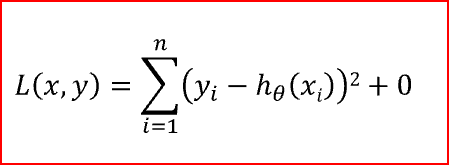when ? is zero
When ? is large, we penalizes the weights and they become close to zero. This results is a very simple model having a high bias or is underfitting.
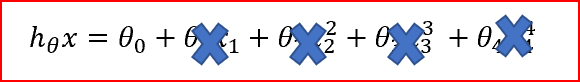when ? is very large
so what is the right value for ? ?
It is somewhere in between 0 and a large value. we need to find an optimal value of ? so that the generalization error is small.
A simple approach would be try different values of ? on a subsample of data, understand variability of the loss function and then use it on the entire dataset.
What is L1 and L2 regularization ?
L1 regularization is also referred as L1 norm or Lasso.
In L1 norm we shrink the parameters to zero. When input features have weights closer to zero that leads to sparse L1 norm. In Sparse solution majority of the input features have zero weights and very few features have non zero weights.
To predict ACT score not all input features have the same influence on the prediction. GPA score has a higher influence on ACT score than BMI of the student. L1 norm will assign a zero weight to BMI of the student as it does not have a significant impact on prediction. GPA score will have a non zero weight as it is very useful in predicting the ACT score.
L1 regularization does feature selection. It does this by assigning insignificant input features with zero weight and useful features with a non zero weight.
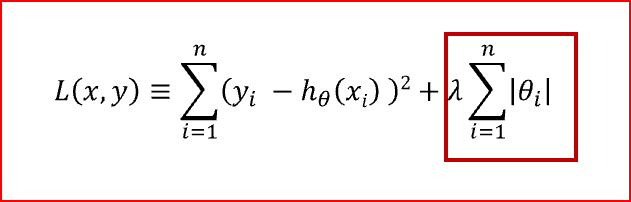L1 regularization
In L1 regularization we penalize the absolute value of the weights. L1 regularization term is highlighted in the red box.
Lasso produces a model that is simple, interpretable and contains a subset of input features
L2 Regularization or Ridge Regularization
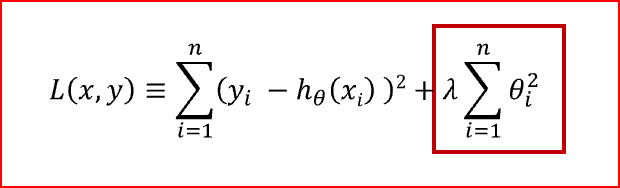L2 Regularization
In L2 regularization, regularization term is the sum of square of all feature weights as shown above in the equation.
L2 regularization forces the weights to be small but does not make them zero and does non sparse solution.
L2 is not robust to outliers as square terms blows up the error differences of the outliers and the regularization term tries to fix it by penalizing the weights
Ridge regression performs better when all the input features influence the output and all with weights are of roughly equal size
Difference between L1 and L2 regularization
L1 Regularization
L1 penalizes sum of absolute value of weights.
L1 has a sparse solution
L1 has multiple solutions
L1 has built in feature selection
L1 is robust to outliers
L1 generates model that are simple and interpretable but cannot learn complex patterns
L2 Regularization
L2 regularization penalizes sum of square weights.
L2 has a non sparse solution
L2 has one solution
L2 has no feature selection
L2 is not robust to outliers
L2 gives better prediction when output variable is a function of all input features
L2 regularization is able to learn complex data patterns
we see that both L1 and L2 regularization have their own strengths and weakness.
Elastic net regularization is a combination of both L1 and L2 regularization.
