WORD VECTORS
Word vectors represent a significant leap forward in advancing our ability to analyse relationships across words, sentences and documents. In doing so, they advance technology by providing machines much more information about words than has previously been possible using traditional representations of words. It is word vectors that make technologies such as speech recognition and machine translation possible. There are many excellent explanations of word vectors, but in this one I want to make the concept accessible to data and research people who aren?t very familiar with natural language processing (NLP).
WHAT ARE WORD VECTORS?
Word vectors are simply vectors of numbers that represent the meaning of a word. For now, that?s not very clear but, we?ll come back to it in a bit. It is useful, first of all to consider why word vectors are considered such a leap forward from traditional representations of words.
Traditional approaches to NLP, such as one-hot encoding and bag-of-words models (i.e. using dummy variables to represent the presence or absence of a word in an observation (e.g. a sentence)), whilst useful for some machine learning (ML) tasks, do not capture information about a word?s meaning or context. This means that potential relationships, such as contextual closeness, are not captured across collections of words. For example, a one-hot encoding cannot capture simple relationships, such as determining that the words ?dog? and ?cat? both refer to animals that are often discussed in the context of household pets. Such encodings often provide sufficient baselines for simple NLP tasks (for example, email spam classifiers), but lack the sophistication for more complex tasks such as translation and speech recognition. In essence, traditional approaches to NLP, such as one-hot encodings, do not capture syntactic (structure) and semantic (meaning) relationships across collections of words and, therefore, represent language in a very naive way.
In contrast, word vectors represent words as multidimensional continuous floating point numbers where semantically similar words are mapped to proximate points in geometric space. In simpler terms, a word vector is a row of real valued numbers (as opposed to dummy numbers) where each point captures a dimension of the word?s meaning and where semantically similar words have similar vectors. This means that words such as wheel and engine should have similar word vectors to the word car (because of the similarity of their meanings), whereas the word banana should be quite distant. Put differently, words that are used in a similar context will be mapped to a proximate vector space (we will get to how these word vectors are created below). The beauty of representing words as vectors is that they lend themselves to mathematical operators. For example, we can add and subtract vectors ? the canonical example here is showing that by using word vectors we can determine that:
king ? man + woman = queen
In other words, we can subtract one meaning from the word vector for king (i.e. maleness), add another meaning (femaleness), and show that this new word vector (king ? man + woman) maps most closely to the word vector for queen.
The numbers in the word vector represent the word?s distributed weight across dimensions. In a simplified sense each dimension represents a meaning and the word?s numerical weight on that dimension captures the closeness of its association with and to that meaning. Thus, the semantics of the word are embedded across the dimensions of the vector.
A SIMPLIFIED REPRESENTATION OF WORD VECTORS
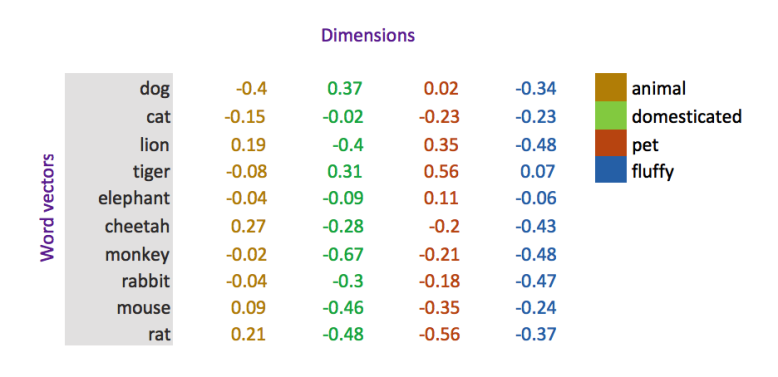
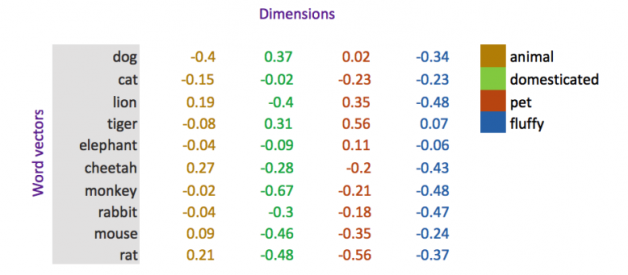
In the figure we are imagining that each dimension captures a clearly defined meaning. For example, if you imagine that the first dimension represents the meaning or concept of ?animal?, then each word?s weight on that dimension represents how closely it relates to that concept.
This is quite a large simplification of word vectors as the dimensions do not hold such clearly defined meanings, but it is a useful and intuitive way to wrap your head around concept of word vector dimensions.
We create a list of words, apply spaCy?s parser, extract the vector for each word, stack them together and then extract two-principal components for visualisation purposes.
import numpy as npimport spacyfrom sklearn.decomposition import PCAnlp = spacy.load(“en”)animals = “dog cat hamster lion tiger elephant cheetah monkey gorilla antelope rabbit mouse rat zoo home pet fluffy wild domesticated”animal_tokens = nlp(animals)animal_vectors = np.vstack([word.vector for word in animal_tokens if word.has_vector])pca = PCA(n_components=2)animal_vecs_transformed = pca.fit_transform(animal_vectors)animal_vecs_transformed = np.c_[animals.split(), animal_vecs_transformed]
Here we simply extract vectors for different animals and words that might be used to describe some of them. As mentioned in the beginning word vectors are amazingly powerful because they allow us (and machines) to identify similarities across different words by representing them in a continuous vector space. You can see here how the vectors for animals like ?lion?, ?tiger?, ?cheetah? and ?elephant? are very close together. This is likely because they are often discussed in similar contexts, for example these animals are big, wild and potentially dangerous ? indeed, the descriptive word ?wild? maps quite closely to this group of animals.
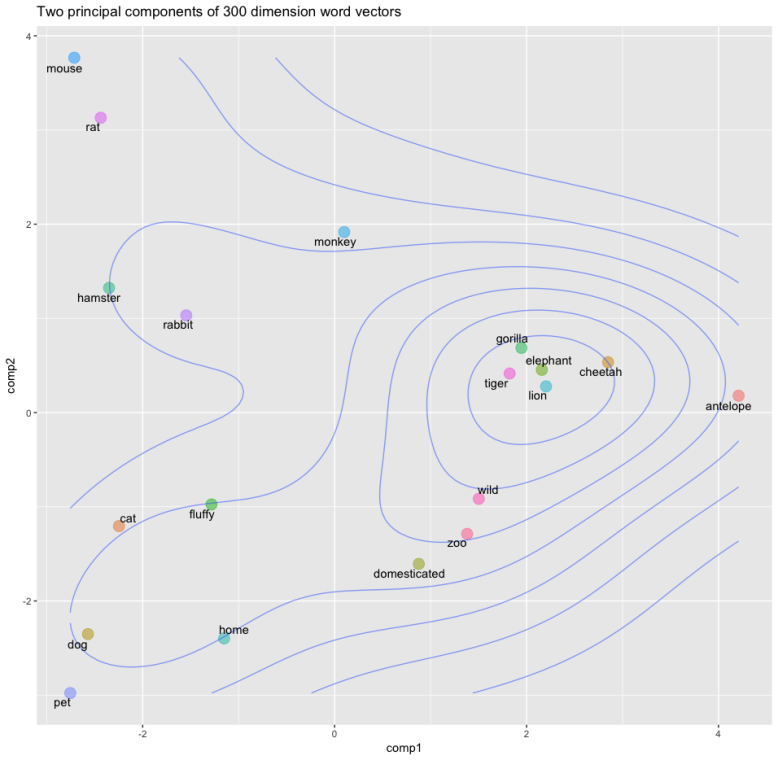
Similar words are mapped together in the vector space. Notice how close cat and dog are to pet, how clustered elephant, lion and tiger are, and how descriptive words also cluster together.
What is also interesting here is how closely the words ?wild?, ?zoo? and ?domesticated? map to one another. It makes sense given that they are words that are frequently used to describe animals, but highlights the amazing power of word vectors!
WHERE DO WORD VECTORS COME FROM?
An excellent question at this point is where do these dimensions and weights come from?! There are two common ways through which word vectors are generated:
- Counts of word / context co-occurrences
- Predictions of context given word (skip-gram neural network models, e.g. word2vec)
*Note: below I describe a high-level word2vec approach to generating word vectors, but a good overview of the count / co-occurence approach can be found here (https://medium.com/ai-society/jkljlj-7d6e699895c4).
Both approaches to generating word vectors build on Firth?s (1957) distributional hypothesis which states:
?YOU SHALL KNOW A WORD BY THE COMPANY IT KEEPS?
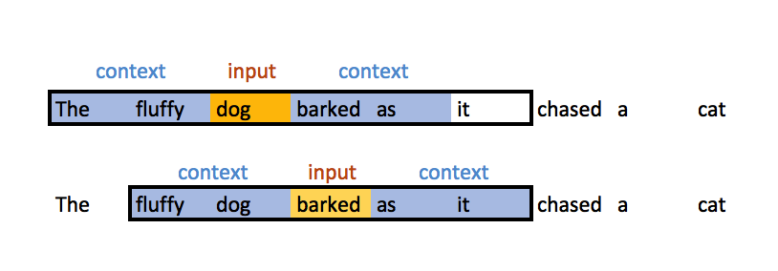
Put differently, words that share similar contexts tend to have similar meanings. The context of a word in a practical sense refers to its surrounding word(s) and word vectors are (typically) generated by predicting the probability of a context given a word. Put differently, the weights that comprise a word vector are learned by making predictions on the probability that other words are contextually close to a given word. This is akin to attempting to fill in the blanks around some given input word. For example, given the input sequence, ?The fluffy dog barked as it chased a cat?, the two-window (two-words preceding and proceeding the focal word) context for the words ?dog? and ?barked? would look like:
I don?t wish to delve into the mathematical details how neural networks learn word embeddings too much, as people much more qualified to do so have explicated this already. In particular these posts have been helpful to me when trying to understand how word vectors are learned:
- Deep Learning, NLP, and Representations (http://colah.github.io/posts/2014-07-NLP-RNNs-Representations/)
- The amazing power of word vectors (https://blog.acolyer.org/2016/04/21/the-amazing-power-of-word-vectors/)
- Word2Vec Tutorial ? The Skip-Gram Model (http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/)
It is useful, however, to touch on the workings of the word2vecmodel given its popularity and usefulness. A word2vec model is simply a neural network with a single hidden layer that is designed to reconstruct the context of words by estimating the probability that a word is ?close? to another word given as input.
The model is trained on word, context pairings for every word in the corpus, i.e.:
(DOG, THE)(DOG), FLUFFY(DOG, BARKED)(DOG, AS)
Note that this is technically a supervised learning process, but you do not need labelled data ? the labels (the targets / dependent variables) are generated from the words that form the context of a focal word. Thus, using the window function the model learns the context in which words are used. In this simple example the model will learn that fluffy and barked are used in the context (as defined by the window length) of the word dog.
One of the fascinating things about word vectors created by word2vec models is that they are the side effects of a predictive task, not its output. In other words, a word vector is not predicted, (it is context probabilities that are predicted), the word vector is a learned representation of the input that is used on the predictive task ? i.e. predicting a word given a context. The word vector is the model?s attempt to learn a good numerical representation of the word in order to minimize the loss (error) of it?s predictions. As the model iterates, it adjusts its neurons? weights in an attempt to minimize the error of it?s predictions and in doing so, it gradually refines its representation of the word. In doing so, the word?s ?meaning? becomes embedded in the weight learned by each neuron in the hidden layer of the network.
A word2vec model, therefore, accepts as input a single word (represented as a one-hot encoding amongst all words in the corpus) and the model attempts to predict the probability that a randomly chosen word in the corpus is at a nearby position to the input word. This means that for every input word there are n output probabilities, where n is equal to the total size of the corpus. The magic here is that the training process includes only the word?s context, not all words in the corpus. This means in our simple example above, given the word ?dog? as input, ?barked? will have a higher probability estimate than ?cat? because it is closer in context ? i.e. it is learned in the training process. Put differently, the model attempts to predict the probability that other words in the corpus belong to the context of the input word. Therefore, given the sentence above (?The fluffy dog barked as it chased a cat?) as input a run of the model would look like this:
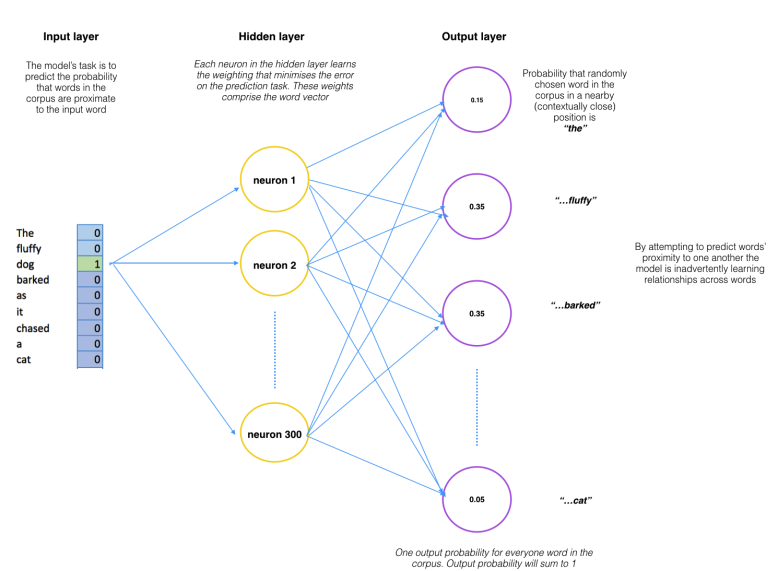
Note: This conceptual NN is a close friend of the diagram in Chris McCormick?s blog post linked to above
The value in going through this process is to extract the weights that have been learned by the neurons of the model?s hidden layer. It is these weights that form the word vector, i.e. if you have a 300 neuron hidden layer you will create a 300-dimension word vector for each word in the corpus. The output of this process, therefore, is a word-vector mapping of size n-input words * n-hidden layer neurons.
NEXT UP?
Word vectors are an amazingly powerful concept and a technology that will enable significant breakthroughs in NLP applications and research. They also highlight the beauty of neural network deep learning and, particularly, the power of learned representations of input data in hidden layers. In my next post I will be using word vectors in a convolutional neural network for a classification task. This will highlight word vectors in practice, as well as how to bring pre-trained word vectors into a Keras model.