Probably one of the most famous algorithms ever, but still lot of people struggles when trying to find an efficient solution. Let me introduce you to the Fibonacci sequence.
Statement
Given a number N return the index value of the Fibonacci sequence, where the sequence is:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
After a quick look, you can easily notice that the pattern of the sequence is that each value is the sum of the 2 previous values, that means that for N=5 ? 2+3 or in maths:
F(n) = F(n-1) + F(n-2)
First implementation
So let?s go directly to the first implementation, we are gonna use a simple loop to achieve our solution.
This is probably the first solution that will come to your mind. The important part here is that we calculate the next number by adding the current number to the old number.
And the good news is that has a O(n) time complexity. Fair enough for the first try right? But let?s try to see some other ways to approach the problem.
Recursive solution
Now let?s see if we can make it look fancier, now we will use recursion to do that.
Easy right? we just solved the problem in 2 lines of code, but let?s take a deeper look and see what?s actually happening.
Base case: we just need to check if the value is less than zero for return the 2 firsts cases.
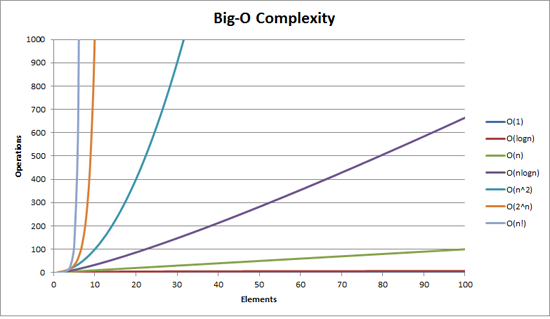
But now the bad news? We have increased the time complexity of our algorithm almost to the worst case. If you take a look at the graphic, you will see the orange color (2^N) time complexity, which means that our current implementation is exponential?
Memoization
Finally, and following the recursive approach we will use memoization to improve our efficiency, but first of all, what?s memoization? as Wikipedia says:
Is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls.
What does that means and why should we take care about that in our implementation? Basically, if we just store the value of each index in a hash, we will avoid the computational time of that value for the next N times.
This change will increase the space complexity of our new algorithm to O(n) but will dramatically decrease the time complexity to 2N which will resolve to linear time since 2 is a constant.
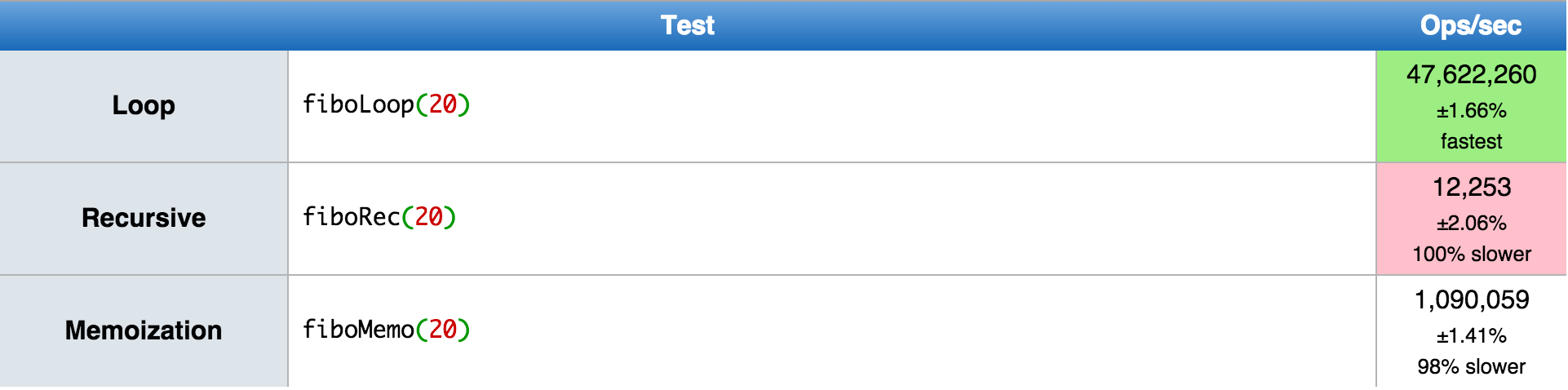
Benchmark
Let?s use 50 as an input number and see how it looks like:
While loop
- Time complexity: O(N)
- Space complexity: Constant
- Function calls: 51
- Time needed: 0.000001ms
Recursion
- Time complexity: O(2^N)
- Space complexity: O(n)
- Function calls: 20.365.011.074
- Time needed: 176.742ms
Memoization
- Time complexity: O(2N)
- Space complexity: O(n)
- Function calls: 99
- Time needed: 0.000001ms
JSPerf results
I have also created a jsPerf demo with the 3 cases, you can take a look here:
Conclusion
This was just an example of how to design, improve and analyze an algorithm, in this case it was the Fibonacci sequence, which is simple enough to understand and surprising to see the performance boost we achieved just with some small changes.