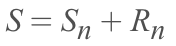It?s also called the Remainder Estimation of Alternating Series.
This is to calculating (approximating) an Infinite Alternating Series:
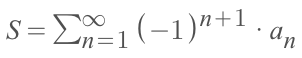
?Jump over to Khan academy for practice: Alternating series remainder
?Refer to The Organic Chemistry Tutor: Alternate Series Estimation Theorem?Refer to Mathonline: Error Estimation for Approximating Alternating Series?Refer to mathwords: Alternating Series Remainder
The logic is:
- First to test the series? convergence.
- If the series CONVERGES, then we can proceed to calculate it by Error Estimation Theorem. Otherwise we aren?t able to.
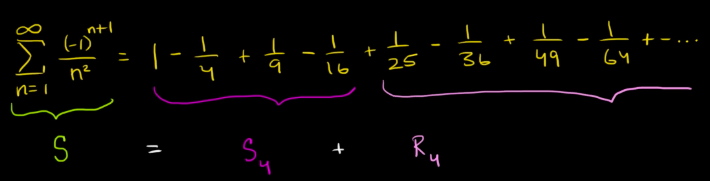
- We can express the series as the sum of partial sums & infinite remainder:
![]()
(? Sn is the first n terms, and Rn is from the n+1 term to the rest terms.)
- And the ?structure? in the partial sum & remainder is:
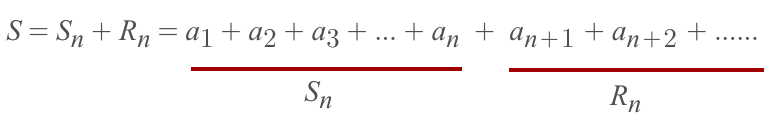
- With a little twist, we will get the whole idea:
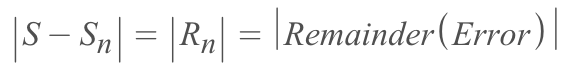
(?Since the Rn is the gap between S & Sn, so we call it The Error)
- ? And the theorem is: The Remainder MUST NOT be greater than its first term:

?Actual sum = Partial sum + Remainder: refer to Khan academy: Alternating series remainder
Sign & Size of Error
?Refer to Khan academy: Alternating series remainder?Refer to Khan academy: Worked example: alternating series remainder
For the Remainder series, its FIRST TERM is always DOMINATING the whole remainder:
- It dominates the remainder?s SIGN: positive or negative.
- It dominates the remainder?s SIZE: the whole remainder?s absolute value CAN?T BE greater than the first term.
Based on the error?s sign, we could tell the approximated series is UNDERESTIMATED or OVERESTIMATED:
- If Error > 0, then the approximated series is Underestimate.
- If Error < 0, then the approximated series is Overestimate.
Bound the Error (accuracy control)
The error bound regards to the accuracy of the approximated series, and we want to control the accuracy before approximation.
?Refer to Khan academy: Worked example: alternating series remainder
We have 2 ways to bound the error in a range:
- Set up how small we want the error to be, or
- Set up how many terms we want to have in the partial sum Sn.
Bound by terms
The Larger n ? The smaller gap ? The lesser Error ? The more accurate.
Strategy:
- We could set the partial sum to include a certain number of terms, etc. 100 terms
- And the first term of Remainder should be the 101st term.
- The error bound, or the error is dominated by the first term.
- So we say the error bound IS the value of the 101st term.
Bound the error
To bound the error in a range, we often say:
- ?Approximate the series to the 2 decimal places?,
- ?Let the error be less than 0.01?,
- ?We want the accuracy within 0.01?
What they mean are the same:
![]()
? And by solving the inequality, we will get the scope for n, then get the Smallest Integer of n in that scope.
Example

Solve:
- First to notice, the partial sum is already set to 100 terms, so we’re to control accuracy by bound the terms.
- So the error should be from the 101st term to infinity.
- But the error bound is actually dominated by the first term of the error.
- So the error bound = the value of 101st term:
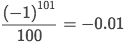
- We could say that: The error bound is negative, and negative error causes overestimation.
Example

Solve:
- It?s clear this is a alternating series.
- So we want to do the alternating series test first, and it passed, which means it converges.
- Since the series converges, we can do further approximation.
- See that we don?t know how many terms are in the partial sum, and only know how much accurate we’d like.
- So we?re to approximate by bound the error, and find out the terms.
- Apply the Error Approximation Theorem, assume the first term of remainder is a_(n+1):
![]()
- Solve out the inequality to get n ? 999,999
- And 999,999 the smallest integer of n to make the series converges with 2 decimal accuracy.