
If someone has told you that Mathematics is not a viable career, tell them to go and look up Grigori Perelman. He is (as of 2019) the one and only person to be credited with solving a Millennium Prize Problem, earning him much notoriety and a cool $1,000,000 (even though he eventually turned down the prize money).
The problem in question, the Poincar Conjecture, is a theorem about the characterization of the 3-sphere, which is the hypersphere that bound the unit ball in four-dimensional space.
For those of you interested in the mathematical terms, here you go:
- A unit sphere is the set of points of distance 1 from a fixed central point. The fixed central point usually refers to a specific point in the space that is has been distinguished as the origin of the space (ie. on a 2D graph the point (0,0) is considered the origin, on a 3D graph the point (0,0,0)).
- A hypersphere is the set of points at a constant distance from a given point, in the (n-1)’th dimension of it?s containing ambient space. For example, a hypersphere in the dimension R (x,y,z plane) would be a sphere, also called a 2-sphere.
- A 3-sphere is analogue of a sphere in a higher dimension and would be a hypersphere in the 4th dimension.
- If you have a 3-sphere with radius 1 and center at the origin in the 4th dimension, then you get a hypersphere that bounds the unit sphere (a sphere of points of distance 1 from a fixed point) in the fourth dimension.
- [Semi-important for below] If you have a loop in a Euclidean space such that you can ?tighten? it (think about a having a circle and decreasing the radius continuously until you have a radius of 0) to a single point where all of the intermediary loops and the final point are all in the set, then the loop can be ?tightened continuously to a point in the space?
In layman’s terms, we think about a space that locally looks like ordinary three-dimensional space, but is connected, finite in size, and lacks any boundaries (a closed 3-manifold). Then the theorem claims that if such a space exists and has the additional property that each loop can be continuously tightened to a point in the space, then it is a three-dimensional sphere.
After nearly a century of effort from mathematicians, Perelman presented a proof of the conjecture in the papers between 2002 and 2003. The proof built upon Richard S. Hamilton?s work, where he showed how to use the Ricci flow on a manifold to prove special cases of the Poincar conjecture. Hamilton extended his work for multiple years but was unable to prove the conjecture conclusively. Using this groundwork, Perelman was able to sketch a proof of a more general conjecture, Thurston?s Geometrization conjecture, completing the Ricci flow program and proving the first Millennium Prize Problem.
On August 22, 2006, the International Congress of Mathematicians awarded Perelman the Fields Medal for his work on the conjecture, but similarly to the million-dollar bounty, he refused the medal. When asked about turning down the prize money, he remained humble, stating he believed his contributions in proving the conjecture was no greater than Hamilton?s.
The Poincar Conjecture and 6 other complex mathematical theories have been dubbed the Millennium Prize Problems by the Clay Mathematics Institute (CMI). Each problem has been described as an ?important classic question that has resisted solutions over the years?, with the first person to devise a solution to each earning $1,000,000 courtesy of the CMI. However, as you saw above, solving these problems is no easy feat. One of the problems has remained unsolved since it?s formulation in 1859 by German Mathematician Bernhard Riemann.
The Riemann Hypothesis, named after the aforementioned German mathematician, is widely considered to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime number, which are used in everything from biology to encryption and quantum mechanics. In order to understand the Riemann Hypothesis, we first need to explain a few key concepts:
- A complex number is of the form a+bi, where i is defined by i=-1. In this form, the real part of a complex number is a, and the imaginary part is bi.
- The Riemann zeta function is a function of a complex variable (a function of complex numbers) defined by the following equation, where s is any complex number other than 1, and whose values are also complex:
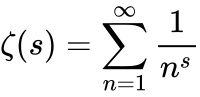
- A ?zero? of a function is an x such that f(x)=0
- The ?trivial zeros? of the Riemann zeta function are all the negative even integers (-2, -4, -6, ?)
- The ?non-trivial zeros? of the Riemann zeta function are all of the other values of s for which ?(s)=0 (ie. s is not a negative even integer).
Now that we have some definitions down pat, we can go ahead and state the Riemann Hypothesis:
The real part of every non-trivial zero of the Riemann zeta function is 1/2
This one (to me at least) is a lot easier to understand than the Poincar Conjecture and does not seem intuitively very difficult. However, it also does not seem to mean much. Really, who cares about when this random function has a value of 0. Well not surprisingly, a lot of mathematicians do, and for a very good reason.
Some numbers have the special property that they cannot be expressed as the product of two smaller numbers (product being multiplication), ie. 2,3,5,7,11, etc. Known as prime numbers, they are in a sense the simplest numbers you can get, forming the building blocks for all other numbers. Frustratingly though, prime numbers do not seem to follow any pattern. 3137 is a prime number, and the next one after that is not until 3163, but then 3167 and 3169 follow in quick succession, all of which are primes. In a nutshell, if you find one prime number, there is no way to tell where the next one is going to be without checking all of the numbers as you go. However, using the Prime Number Theorem (PNT), you can find how many prime numbers there are below a certain threshold.
The Prime Number Theorem is just an estimation, with different values giving a different probability of being correct, but never 100% certainty. However, understand the assumption that the Reimann hypothesis is true, you can create a mathematical approximation combining the Prime Number Theorem and the non-trivial zeros of the Riemann zeta function to error-correct the internal components, providing the ?best possible? bound for the error term in the Prime Number Theorem. If it were possible to prove the Reimann Hypothesis completely, this would give the PNT the ability to provide incredibly close estimates to the actual value, opening up many possibilities in different branches of mathematics. In fact, there are many important hypotheses that being with ?If the Riemann Hypothesis is true, then ??, so solving this problem would instantly validate all of the subsequent conjectures as well.
Another interesting Millenium problem has gained a bit of facetime recently thanks to the 2017 film Gifted, which focused on the brother and daughter of a female mathematician dedicated to solving the Navier?Stokes problem. The film does not touch on the problem much, probably due to its complexity, but it is worth exploring none the less.
The Navier-Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier?Stokes equations, one of the pillars of fluid mechanics. Imagine waves following our boat as we drive across a lake, or turbulent air currents following flights in a modern jet. Mathematicians and physicists believe that an explanation for and prediction of both the breeze and the turbulence can be found through an understanding of the solutions to the Navier-Stokes equations.
While the Navier-Stokes existence and smoothness problem is a very broad range of questions to be solved, the actual Millenium problem focuses on a solution for one specific statement of the problem:
In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier?Stokes equations.
In order to claim victory, you either need to provide a valid counter-example, prove the above statement conclusively. A solution to this problem would help gain a better understanding of the world we live in, both from a scientific and engineering standpoint. The equations can be used to model the weather, ocean currents, water flowing in a pipe and air flow around a wing. Using them can, amongst other things, aid in the design of aircraft and cars, the study of blood flow, the design of power stations, and the analysis of pollution.
There are 4 other Millenium Problems, all very interesting to explore, and very difficult to prove. However, I like to keep my articles short, so I?ll leave those 4 for another time. I will, however, note that my personal favourite is the P versus NP Problem, a major unsolved problem in computer science (my current degree). It simply asks whether every problem whose solution can be quickly verified can also be solved quickly. Of course, there are many definitions that go around that statement in order to provide some clarity, but that?s one for my next article.
In the meantime, if you are interested in reading about any of the Millenium Problems (or fancy taking a shot at solving one), there are listed here of the Clay Mathematics Institute website. And if you want me to do a more in-depth review of one of the problems, trying my best to convert the complex mathematics into something I (and hopefully you) can understand, be sure to leave a comment letting me know which one you want me to do.

