In my second series of Data Structures and Big O Notation, I am going to talk about Hash Tables, which are also known as Hash Maps, Maps, or Dictionaries. Objects in JavaScript are a type of Hash Tables as well. Similarly, as in my previous blog , I will go in-depth of explaining what advantages or disadvantages Hash Tables have in terms of time and space complexity, compare to other data structures. But first, what exactly isHash Table?
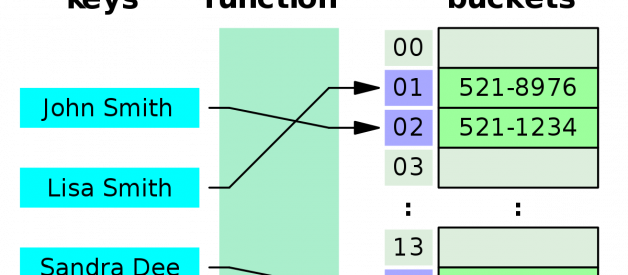
Hash Table is a data structure that has ability to map keys to values. To think of it as real life analogies, we can think of a KEY as computer science class and VALUES as students of the class. A Value is a property of a key. You might wonder, how are they assigned to each other? Hash Tables consist of two parts: an array (usually array of Linked List) and a hash function. The array is where we hold our data, and hash function is what helps us to decide where our inputted data will be saved in our computer memory. The efficiency of mapping solely depends on how fast the hash function is. The way function works is that it maps key to an index in the array, while the value is a data that lives or is inserted at that index.
source: https://en.wikipedia.org/wiki/Hash_table
Another example of hash tables can be a bookshelf that has size of 10, meaning our books need to be stored somewhere within these 10 array or hash buckets. Just sake of an example, lets consider that the way our mapping algorithm works is that it counts characters of book title and then divides total to the size of the hash table. Finally, if there is a remainder, assign that number location to our value. For example, ?Paradise Lost? has 12 characters, which means that 12%10 with module operator returns remainder of 2, and book with the title ?Paradise Lost? goes to 2nd shelf. If we take the book ?Under the Volcano?, which has 15 characters, it means that it?s address location is going to be 5th shelf since we have a reminder of 5. Pretty easy. We can easily do these computation and implement elements in our hash table.
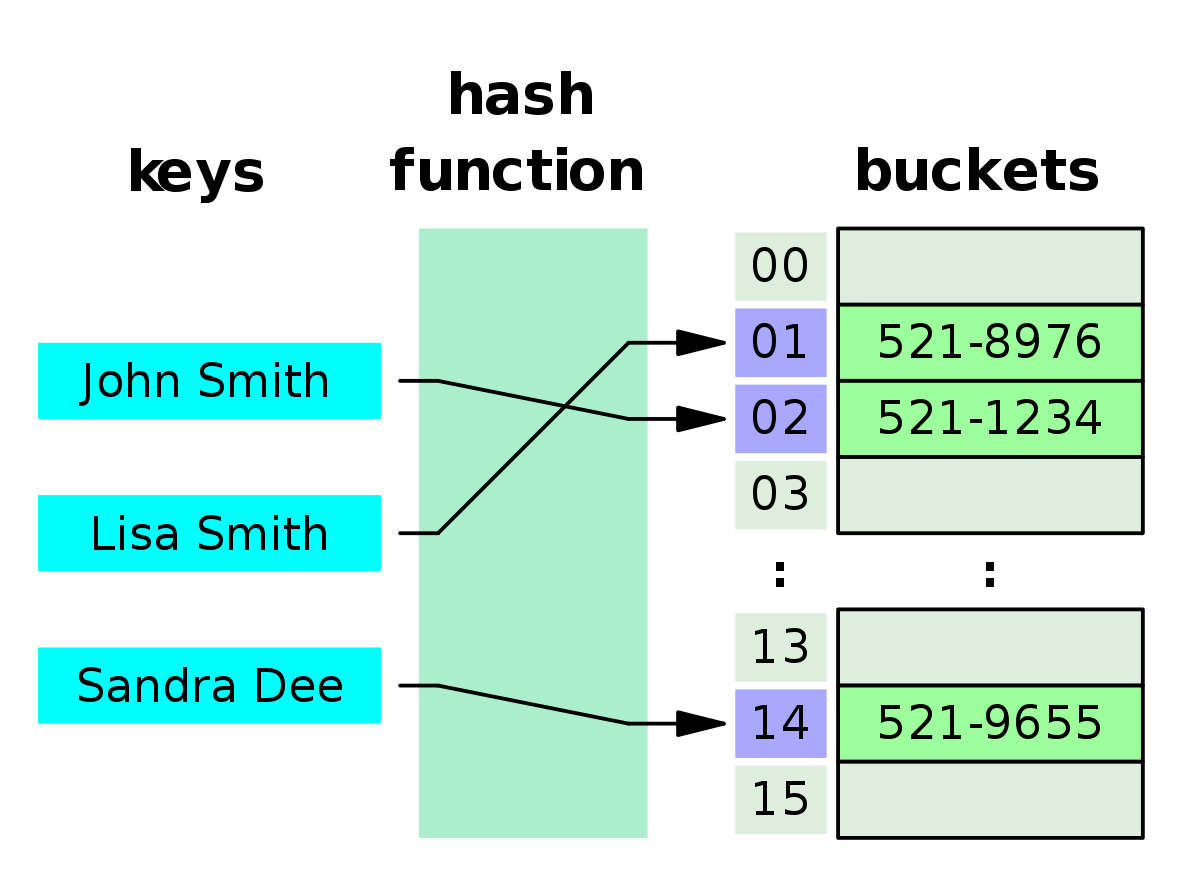
Collision
As mentioned before, Hash Tables is a kind of data structure used to implement an associative array, such as array of linked lists. In the best scenario, the hash function will assign each key to a unique hash bucket, however sometimes two keys will generate identical hash causing both keys to point to the same bucket. In fact, a hash function will almost always input multiple elements to the same hash bucket because the size of our dataset will usually be larger than the size of our hash table. The best way to avoid collision is to use a good hash function that distributes elements uniformly over the hash table. However, the time to lookup the element will be slow O(n). There are multiple ways to deal with collision, such as separate chaining, open addressing, 2-choice hashing. You can learn more about it here.
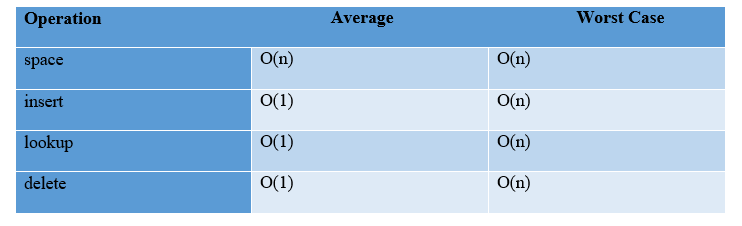
Big O Notation in Hash Tables.
source: https://chercher.tech/java-data-structures/hashtable
In terms of manipulating dataset, such as lookup, insertion, deletion, and search, Hash tables have huge advantage since it has key ? value based structure. If every element is where it should be the the search can use a single comparison to discover the presence of an element. It means that searching for the element takes same amount of time as searching for the first element of an array, which is a constant time or O(1). However, if our dataset is bigger than hash table collisions occur and we need to deal with them using different methods. It takes also constant time to insert and delete an element because the hash function determines where to save or remove it.
References:
- https://en.wikipedia.org/wiki/Hash_table
- https://runestone.academy/runestone/books/published/pythonds/SortSearch/Hashing.html
- https://guide.freecodecamp.org/computer-science/data-structures/hash-tables/
- https://www.cs.auckland.ac.nz/software/AlgAnim/hash_tables.html
