Conceived by Edsger W. Dijsktra in 1956 and published three years later, Dijkstra?s algorithm is a one of the most known algorithms for finding the shortest paths between nodes in a graph. This algorithm is applied in a lot of domains. For example, once you have represented road networks in a graph, it becomes easy to calculate shortest paths inside this graph by applying Dijkstra?s algorithm.
In Pseudocode, Dijkstra?s algorithm can be translated like that :

In this tutorial, you?re going to learn how to implement Disjkstra?s Algorithm in Java. In a first time, we need to create objects to represent a graph before to apply Dijkstra?s Algorithm.
1. Represent Edges
In a graph, Edges are used to link two Nodes. So, an Edge is linked to two nodes and have a length that is an integer here. It?s useful to represent a distance for example in road networks.
package com.ssaurel.dijsktra;public class Edge { private int fromNodeIndex; private int toNodeIndex; private int length; public Edge(int fromNodeIndex, int toNodeIndex, int length) { this.fromNodeIndex = fromNodeIndex; this.toNodeIndex = toNodeIndex; this.length = length; } public int getFromNodeIndex() { return fromNodeIndex; } public int getToNodeIndex() { return toNodeIndex; } public int getLength() { return length; } // determines the neighbouring node of a supplied node, based on the two nodes connected by this edge public int getNeighbourIndex(int nodeIndex) { if (this.fromNodeIndex == nodeIndex) { return this.toNodeIndex; } else { return this.fromNodeIndex; } }}
2. Represent Nodes
Now, it?s time to represent Nodes. A Node must have a list of Edge that are linked to it. Besides, it must have a field to define if the Node has been visited or no. It will be useful when we will apply Dijkstra?s Algorithm to calculate shortest paths in the graph. Last, we need to define a distanceFromSource field that will represent the result for that Node of the algorithm.
package com.ssaurel.dijsktra;import java.util.ArrayList;public class Node { private int distanceFromSource = Integer.MAX_VALUE; private boolean visited; private ArrayList<Edge> edges = new ArrayList<Edge>(); // now we must create edges public int getDistanceFromSource() { return distanceFromSource; } public void setDistanceFromSource(int distanceFromSource) { this.distanceFromSource = distanceFromSource; } public boolean isVisited() { return visited; } public void setVisited(boolean visited) { this.visited = visited; } public ArrayList<Edge> getEdges() { return edges; } public void setEdges(ArrayList<Edge> edges) { this.edges = edges; }}
3. Represent a Graph
Now that we have Edges and Nodes, we can represent a Graph that must contain Edges and Nodes. In the constructor, we take an array of Edges and we build the Graph by creating corresponding Nodes. The Dijkstra?s Algorithm is implemented in the calculateShortestDistances() method. It?s really the application of the Pseudocode algorithm displayed previously. Our Graph class is like that :
package com.ssaurel.dijsktra;import java.util.ArrayList;// now we must create graph object and implement dijkstra algorithmpublic class Graph { private Node nodes; private int noOfNodes; private Edge edges; private int noOfEdges; public Graph(Edge edges) { this.edges = edges; // create all nodes ready to be updated with the edges this.noOfNodes = calculateNoOfNodes(edges); this.nodes = new Node[this.noOfNodes]; for (int n = 0; n < this.noOfNodes; n++) { this.nodes[n] = new Node(); } // add all the edges to the nodes, each edge added to two nodes (to and from) this.noOfEdges = edges.length; for (int edgeToAdd = 0; edgeToAdd < this.noOfEdges; edgeToAdd++) { this.nodes[edges[edgeToAdd].getFromNodeIndex()].getEdges().add(edges[edgeToAdd]); this.nodes[edges[edgeToAdd].getToNodeIndex()].getEdges().add(edges[edgeToAdd]); } } private int calculateNoOfNodes(Edge edges) { int noOfNodes = 0; for (Edge e : edges) { if (e.getToNodeIndex() > noOfNodes) noOfNodes = e.getToNodeIndex(); if (e.getFromNodeIndex() > noOfNodes) noOfNodes = e.getFromNodeIndex(); } noOfNodes++; return noOfNodes; } // next video to implement the Dijkstra algorithm !!! public void calculateShortestDistances() { // node 0 as source this.nodes[0].setDistanceFromSource(0); int nextNode = 0; // visit every node for (int i = 0; i < this.nodes.length; i++) { // loop around the edges of current node ArrayList<Edge> currentNodeEdges = this.nodes[nextNode].getEdges(); for (int joinedEdge = 0; joinedEdge < currentNodeEdges.size(); joinedEdge++) { int neighbourIndex = currentNodeEdges.get(joinedEdge).getNeighbourIndex(nextNode); // only if not visited if (!this.nodes[neighbourIndex].isVisited()) { int tentative = this.nodes[nextNode].getDistanceFromSource() + currentNodeEdges.get(joinedEdge).getLength(); if (tentative < nodes[neighbourIndex].getDistanceFromSource()) { nodes[neighbourIndex].setDistanceFromSource(tentative); } } } // all neighbours checked so node visited nodes[nextNode].setVisited(true); // next node must be with shortest distance nextNode = getNodeShortestDistanced(); } } // now we’re going to implement this method in next part ! private int getNodeShortestDistanced() { int storedNodeIndex = 0; int storedDist = Integer.MAX_VALUE; for (int i = 0; i < this.nodes.length; i++) { int currentDist = this.nodes[i].getDistanceFromSource(); if (!this.nodes[i].isVisited() && currentDist < storedDist) { storedDist = currentDist; storedNodeIndex = i; } } return storedNodeIndex; } // display result public void printResult() { String output = “Number of nodes = ” + this.noOfNodes; output += “nNumber of edges = ” + this.noOfEdges; for (int i = 0; i < this.nodes.length; i++) { output += (“nThe shortest distance from node 0 to node ” + i + ” is ” + nodes[i].getDistanceFromSource()); } System.out.println(output); } public Node getNodes() { return nodes; } public int getNoOfNodes() { return noOfNodes; } public Edge getEdges() { return edges; } public int getNoOfEdges() { return noOfEdges; }}
In the printResult() method, we have just to iterate on the Nodes? array and display the distanceFromSource property value.
4. Assemble the puzzle in a Main class
Now, it?s time to test our implementation of the Dijkstra?s Algorithm. So, we consider the following graph :
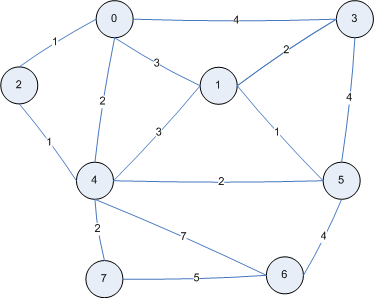
We define that graph in our Main class and then we have just to call the calculateShortestDistances() method. Last, we need to print the result of the algorithm.
package com.ssaurel.dijsktra;public class Main { public static void main(String args) { Edge edges = { new Edge(0, 2, 1), new Edge(0, 3, 4), new Edge(0, 4, 2), new Edge(0, 1, 3), new Edge(1, 3, 2), new Edge(1, 4, 3), new Edge(1, 5, 1), new Edge(2, 4, 1), new Edge(3, 5, 4), new Edge(4, 5, 2), new Edge(4, 6, 7), new Edge(4, 7, 2), new Edge(5, 6, 4), new Edge(6, 7, 5) }; Graph g = new Graph(edges); g.calculateShortestDistances(); g.printResult(); // let’s try it ! }}
Result is detailed in the following figure.
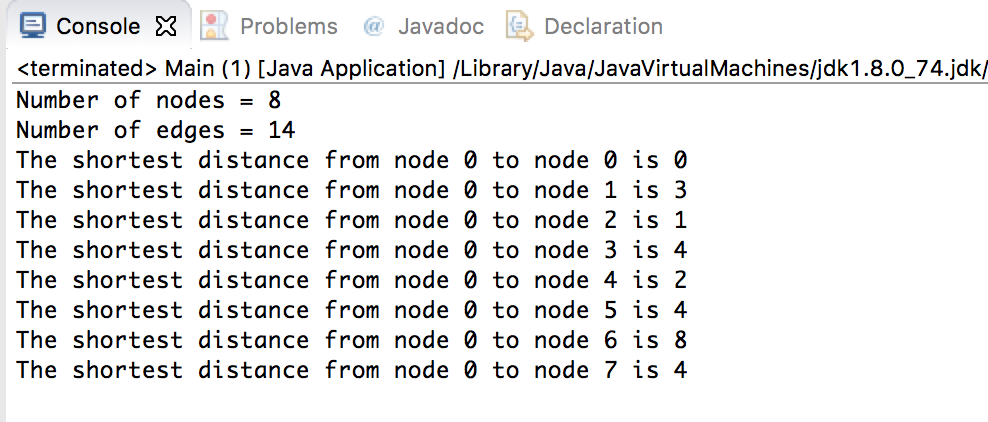
Like you can see, our implementation works well !
5. Bonus
As a Bonus, you can enjoy the following tutorial in video :


