Binary search can be significantly better than the linear search while talking about the time complexity of searching( given the array is sorted).
Rather than eliminating one by one element in every step we can eliminate half of the element in one step.
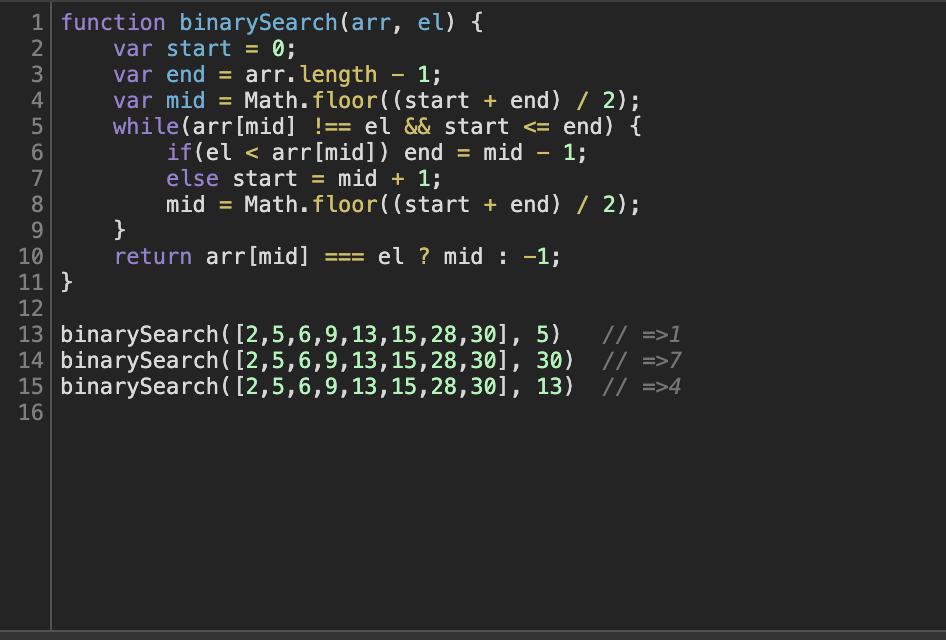
Code Solution
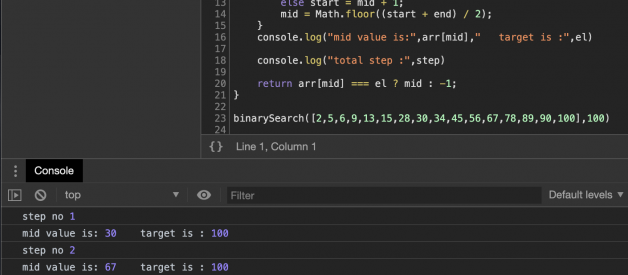
In the above example(line 14) how is this searching:
step1. [2,5,6,9,13,15,28,30] //=>mid value is: 9 target is : 30step2. [13,15,28,30] //=> mid value is: 15 target is : 30step3. [28,30] // => mid value is: 28 target is : 30step4. [30] //=> mid value is: 30 target is : 30
So in step one, the mid-value is the rounded down value of (start+end)/2 that is ?9?, then we compare our target value that is 30 whether this is less than or greater than our mid-value(i.e. ?9?). According to our comparison, in the next step, we eliminate half of the element. And the process continues until it finds our required element (if our element is not there it returns -1 in above code).
Big O of Binary Search
O(log n) => worse and average caseO(1) => Best case
Let’s see an example where there are 16 elements in an array. In our program, we are printing ?steps? in every iteration so that is is easy to visualize what?s going on.
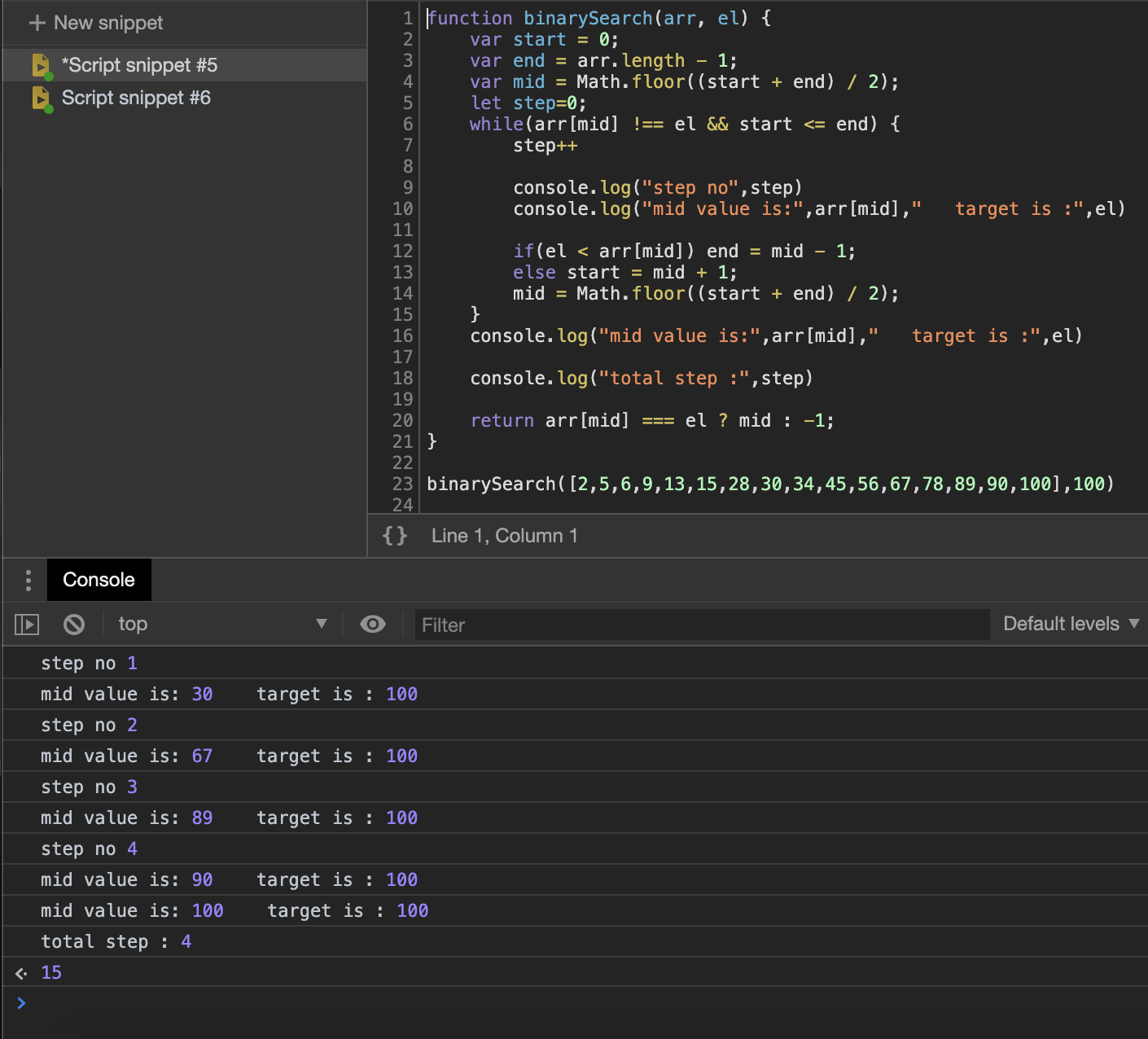
So we see for 16 elements we see the worse case to search an element is 4 steps that can be expressed in log base 2 as following:
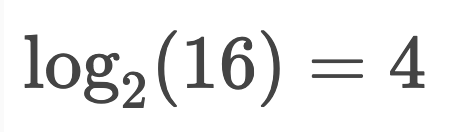log calculation
Similarly, for 32 elements lets see the steps taken.
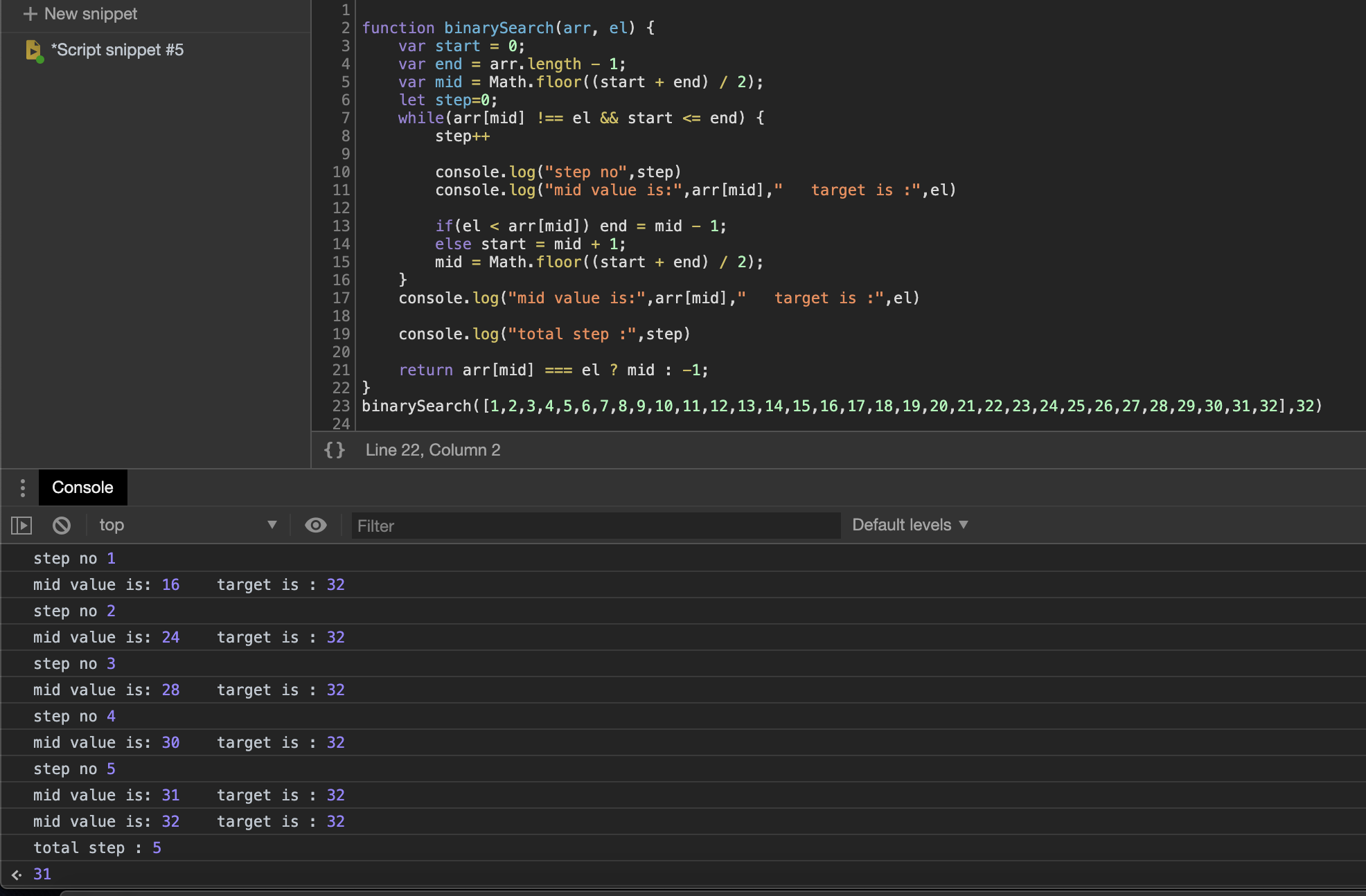
Just 5 steps? We doubled the length of the element.
So, for the double number of elements than 16(16*2=32), our step just increased by +1. And we can relate this relation in a log as follows:
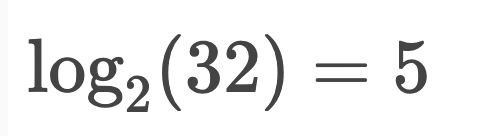
So, by comparing the above results, we can say that the number of steps in the binary search algorithm is directly related to the logarithmic of its number of elements. Hence we can say Big-O run time of binary search is O(log n).
GRAPH OF BIG ?O?
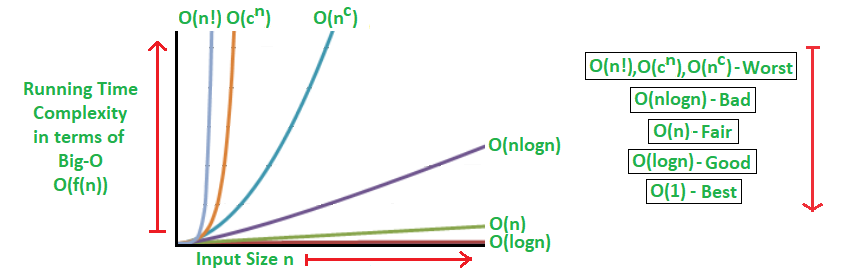
Conclusion
So, binary search is far more faster-searching algorithm than linear searching if the array is sorted. And its Big-O run time is O(log n).
