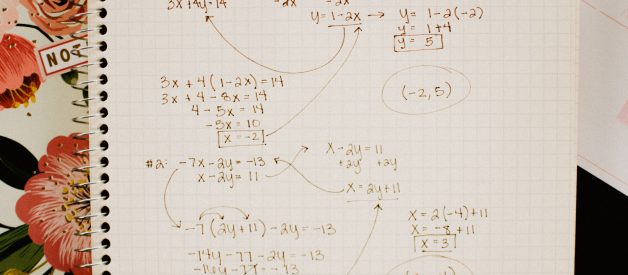Oh, the fundamentals. They don?t call them fundamental by accident. And among one of the most fundamental algebra concepts are Systems of Equations. So if all those x?s and y?s are getting your eyes crossed, fear not. This quick guide will have you straightened out in no time.

Understanding Systems of Equations
Before you jump into learning how to solve for those unknowns, it?s important to know exactly what these solutions mean.
What is a System of Equations?
A System of Equations is exactly what it says it is. It?s a system, meaning 2 or more, equations. When you first encounter system of equations problems you?ll be solving problems involving 2 linear equations. That means your equations will involve at most an x-variable, y-variable, and constant value.
Eventually (perhaps in algebra 2, precalculus, or linear algebra) you?ll encounter more complicated systems. These may involve higher-order functions like quadratics, more than two equations in the system, or equations involving x, y, and z variables (these equations represent planes in 3D space).
But no matter how complicated your system gets, your solution always represents the same concept: intersection. For example, the solution to a system of two linear equations, the most common type of system, is the intersection point between the two lines.
Potential Solutions
As you may already realize, not all lines will intersect in exactly one point. Parallel lines by definition will never intersect, therefore they have no solution. You also may encounter equations that look different, but when reduced end up being the same equation. In this case, you?ll have infinitely many solutions.
The Graphing Method
The easiest and most visual way to find the intersection of a system is by graphing the equations on the same coordinate plane.
To see examples on how to solve a system of linear equations by graphing as well as examples of ?no solution? and ?infinitely many solutions? check out my video tutorial below.
Subscribe to Math Hacks on YouTube
The Substitution Method
Of course, graphing is not the most efficient way to solve a system of equations. That?s why we have a couple more methods in our algebra arsenal.
The first is the Substitution Method. In this method, you isolate a variable in one of your equations and plug that relationship into the other equation. This will provide you with an equation with only one variable, meaning that you can solve for the variable. Once you know the value of one variable, you can easily find the value of the other variable by back-solving.
For more information on how to solve a system using the Substitution Method, check out this tutorial.
Subscribe to Math Hacks on YouTube
The Elimination Method
If the Substitution Method isn?t your cup of tea, you have one last method at your disposal: the Elimination Method.
In this method, you?ll strategically eliminate a variable by adding the two equations together. In order to do this, you?ll often have to multiply one or both equations by a value in order to eliminate a variable. Once you have added the equations and eliminated one variable, you?ll be left with an equation that has only one type of variable in it. Which is handy because you can then solve for that variable. Once you solve for one variable you can plug in the resulting value into one of the original equations to find the value of the other variable.
For a walk-through of exactly how this works, check out my video on using the Elimination Method to solve a system.
Subscribe to Math Hacks on YouTube
And that?s your introduction to Systems of Equations. For more tutorials on how to solve more advanced systems of equations including how to solve systems of three equations using back-solving and matrices, subscribe to the Math Hacks Channel and follow me here on Medium!
? STAY CONNECTED ?
YouTube | Instagram | Facebook | Twitter