Calculating area for polar curves, means we’re now under the Polar Coordinateto do integration.And instead of using rectangles to calculate the area, we are to use triangles to integrate the area for a curve.
? Back to Polar functions (Differential Calc)
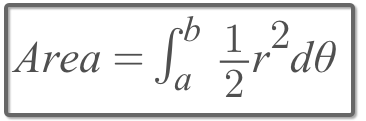
There?re a few notable differences for calculating Area of Polar Curves:
- It?s now under the Polar Coordinate.
- It?s using Circle Sectors with infinite small angles to integral the area.
- It?s the area between the function graph and a RAY or two RAYS from the origin.
? Practice at Khan academy: Area bounded by polar curves
Refer to Khan Academy: Area bounded by polar curves
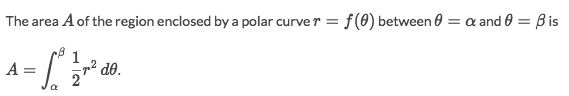
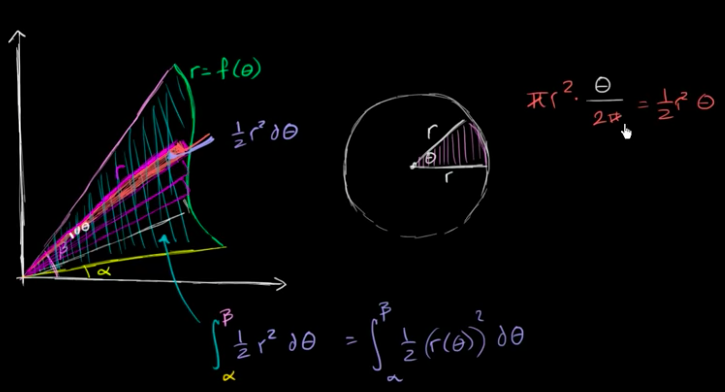
Finding the right boundaries
The most tricky part in Polar system, is finding the right boundaries for ?, and it will be the first step for polar integral as well.
Refer to youtube: Finding Area In Polar Coordinates
Why is this?
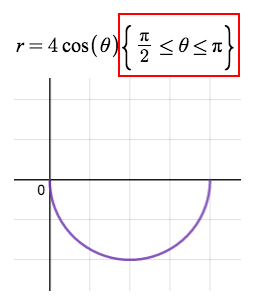
Better to try out on Desmos.com, to see if the interval produces the right shape.
Example
Find out the boundaries of ? for integrating the shaded area:
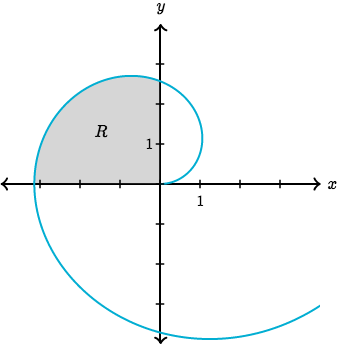
Solve:
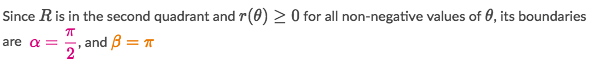
Example
Find out the boundaries of ? for both of the polar curves:
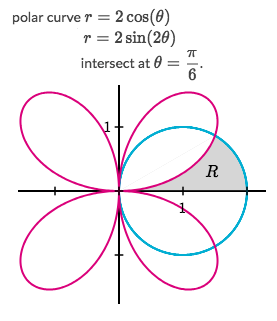
Solve:
- Obviously, for the shading area, both of the curves start at ? = 0 and end at intersection ? = ?/6
Example
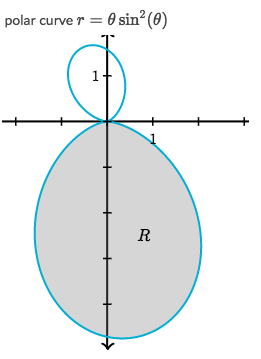
Solve:
- Start thinking as we?re drawing the graph: the r starts drawing at 0, all the way down for a round and goes back to 0.
- Since it goes counter-clockwise, so it?s obvious r goes from ? then takes a round back to 2?.
- So the boundaries are ? and 2?
Example
Find out the boundaries of ? for integrating the shaded area:
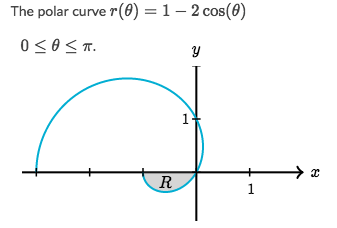
Solve:
- Let?s look at the drawing track: It starts at r = -1 ends at r = 0.
- So we?re to find out the ?-value for the start of r and end of r:
- When r = -1, from the equation we get ? = 0
- When r = 0, from the equation we get ? = ?/3
- Therefore, the boundaries are:
![]()
Example
Find out the boundaries of ? for integrating the shaded area:
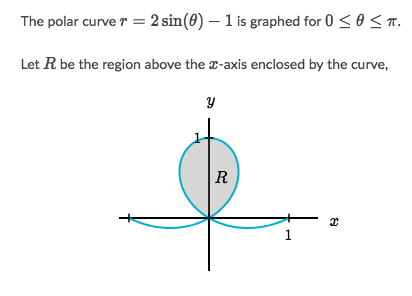
Solve:
- Notice that, for the range ? ? [0,?], it makes r negative: sin(?)-1 = -1and sin(0)-1 = -1.
- But in this case, r starts at 0 and ends at 0, not negative value,
- so we?re gonna despise the given range, and compute the ?-value for r=0:
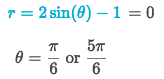
- And the boundaries for ? is ?/6 and 5?/6.
Area between two Polar Curves
Example
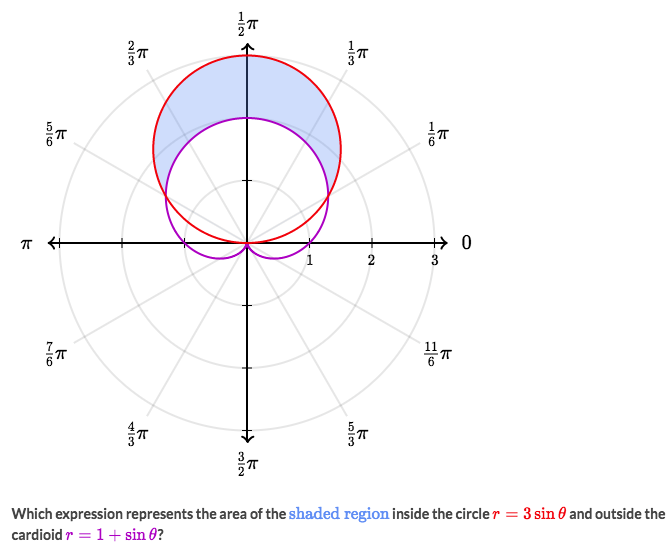
Solve:
- First to notice, the boundaries are at two function?s intersects.
- So let 3sin? = 1+sin?, to get ? = ?/6 and 5?/6, which are the boundaries.
- Within the boundaries, the area asked could be calculated by subtracting the smaller area form bigger one.
- So the area is:
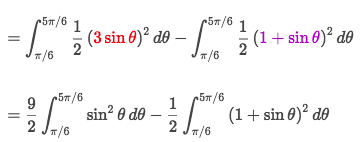
Example
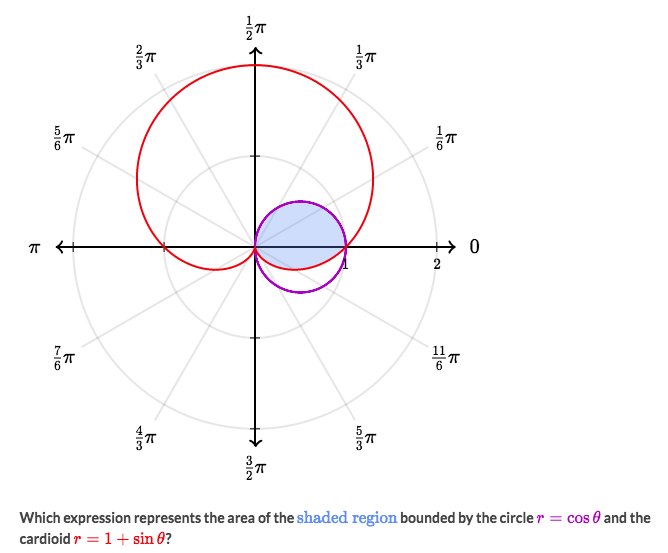
Solve:
- It?s bit tricky to find the boundaries.
- In this case, it?s not subtracting one area from another, but adding two small areas:
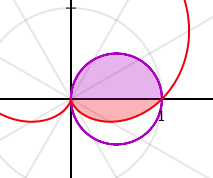
- As showed above, for the cos? shape, its boundaries are same with Quadrant-1: [0, ?/2]
- For the 1+sin? shape, its boundaries are same with Quadrant-4: [3?/2, 2?]
- So the shaded region is:
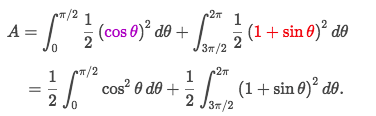
Example
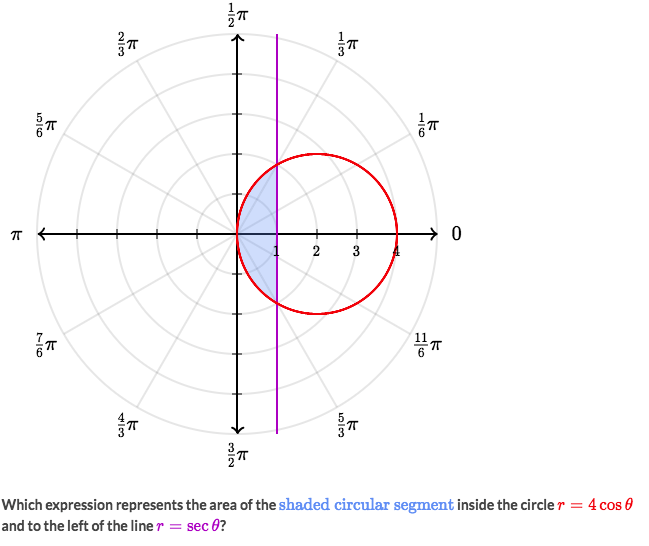
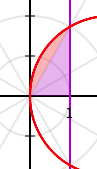
Solve:
- Another tricky one to combine areas.
- Figure out the combination areas as below:
- So the total area is:
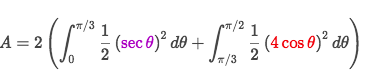
Example
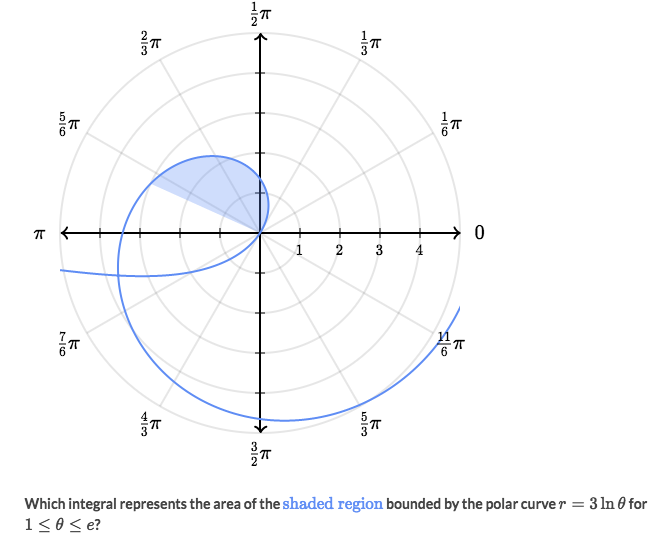
Solve:


