The Taylor expansion is one of the most beautiful ideas in mathematics. The intuition is simple: most functions are smooth over ranges we?re interested in. And polynomials are also smooth. So for every smooth function, we should be able to write down a polynomial that approximates it pretty well.
And in fact, if our polynomial contains enough terms it will exactly equal the original function. Since polynomials are easier to work with than almost any other kind of function, this usually turns hard problems into easy ones.
The Taylor formula is the key. It gives us an equation for the polynomial expansion for every smooth function f. However, while the intuition behind it is simple, the actual formula is not. It can be pretty daunting for beginners, and even experts have a hard time remembering if they haven?t seen it for a while.
In this post, I?ll explain a quick and easy trick I use to re-derive the Taylor formula from scratch whenever I have trouble remembering it.
Starting from Scratch
The idea behind the Taylor expansion is that we can re-write every smooth function as an infinite sum of polynomial terms. The first step is therefore to write down a general nth-degree polynomial. Here it is:
![]()
Where a0, a1, ? are coefficients on each polynomial term, and c is a constant that represents where along the x-axis we want to start our approximation (if we don?t care where we start, just let c = 0, which is technically known as a Maclaurin rather than a Taylor). This series ? known as a ?power series? ? can be written in closed form as the following:
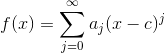
The goal here is to find a clever way to find the coefficients a0, a1, ? in that equation, given some function f and an initial value of c. Here is the logic for doing that. Polynomials are smooth, so that guarantees they?re differentiable. That is, we can calculate the first, second, third and so on derivatives of them.
So starting with our polynomial above, let?s take the first few derivatives of it, like this:
![]()
![]()
![]()
![]()
Clearly we?re seeing a pattern already. We?ll use that in a minute. Now that we have n derivatives of f, let?s evaluate them for some number that will cause most of their terms to drop away. This is the key step. If we?re clever, we?ll notice that if we evaluate them at x = c, most of their terms will go to zero. That will leave behind only the coefficients a1, a2, ? multiplied by some constant. So here?s that step:
![]()
![]()
![]()
![]()
![]()
![]()
Now we have a set of simple equations we can solve for a1, a2, ? Simply divide both sides by n!. That gives us the following:
![]()
![]()
![]()
![]()
![]()
![]()
The pattern here is beautiful. The nth coefficient is just the nth derivative of the original function, evaluated at c, divided by n factorial. Now we have our n coefficients. The next step is to plug them back into our beginning expression for a general nth-degree polynomial, like this:
![]()
![]()
This equation is what we?re looking for. It gives a polynomial expansion for every smooth function f. We just need to calculate the first n derivatives of f, evaluate them at c, divide each one by n!, and sum up these terms. The result will be a good approximation to our original function. The more terms we add on, the more accurate the polynomial approximation will be.
The Result: the Taylor Formula
The final step is to write this infinite series in closed form. This is the last step in the trick for remembering the formula. Writing the above as a summation, we get our final result:
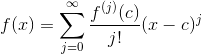
The lesson here is simple: don?t waste your time learning formulas. Learn methods. If you can remember the basic logic of where the Taylor expansion comes from, you can quickly and easily re-derive the formula from scratch.

