Amortized time is the way to express the time complexity when an algorithm has the very bad time complexity only once in a while besides the time complexity that happens most of time. Good example would be an ArrayList which is a data structure that contains an array and can be extended. Other definition from Stack Overflow is average time taken per operation, if you do many operations.
When ArrayList hits the array capacity in it, then it create a new array with the doubled size of the old array and copy all the items in the old array to the new array. In ArrayList, two time complexities exist; one is O(1) and the other is O(n).
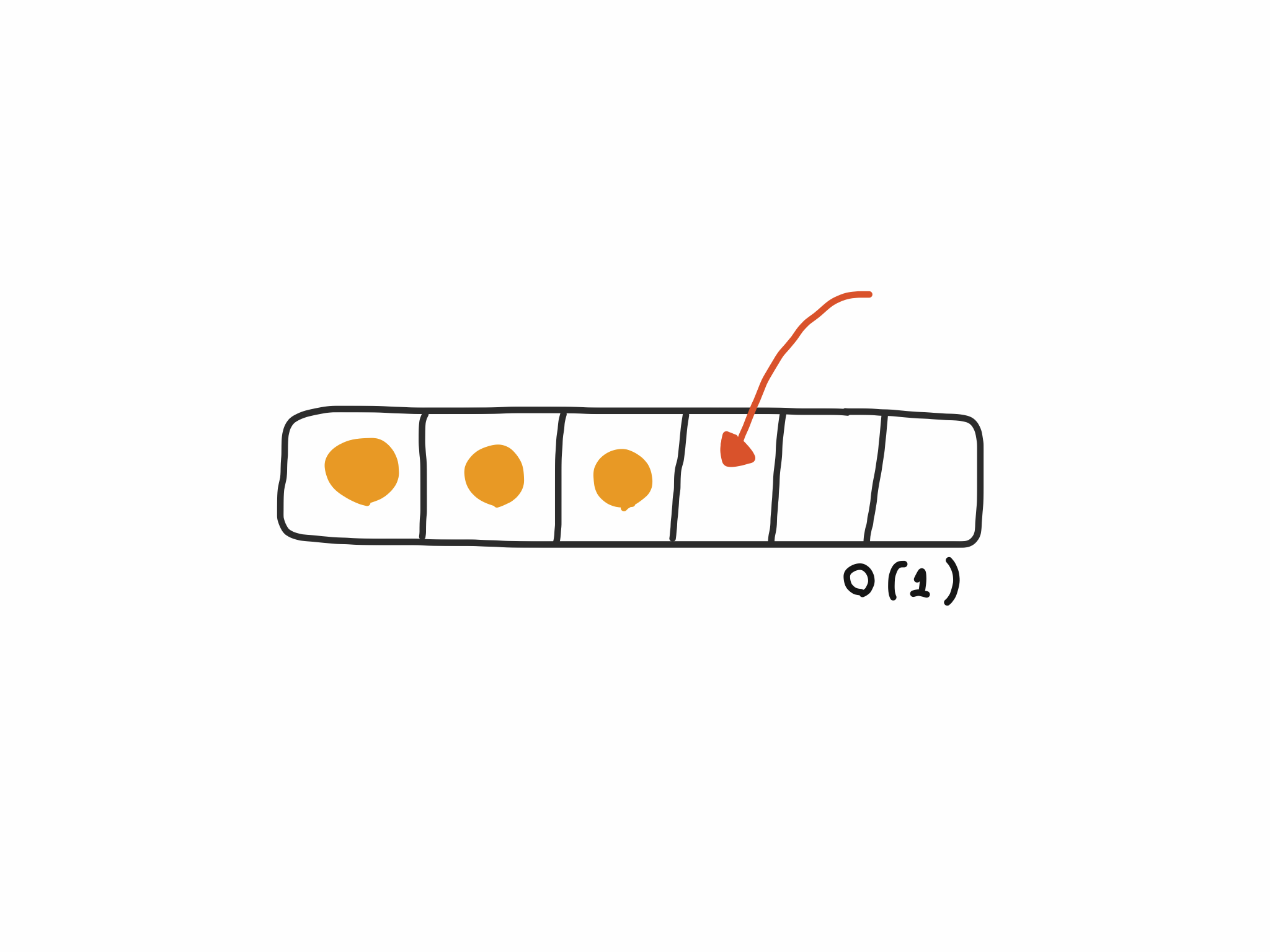
When the array in it hasn?t reached its capacity and still has enough space to insert items
To insert an item to the array in this case, we just need to put the item after the last item. We still have space to insert items.
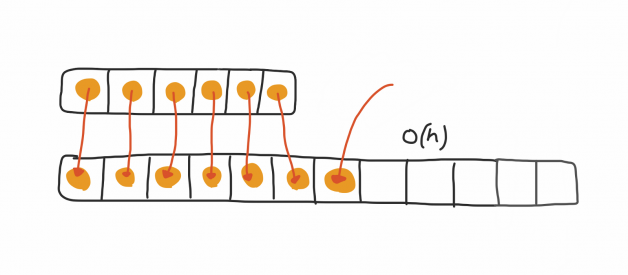
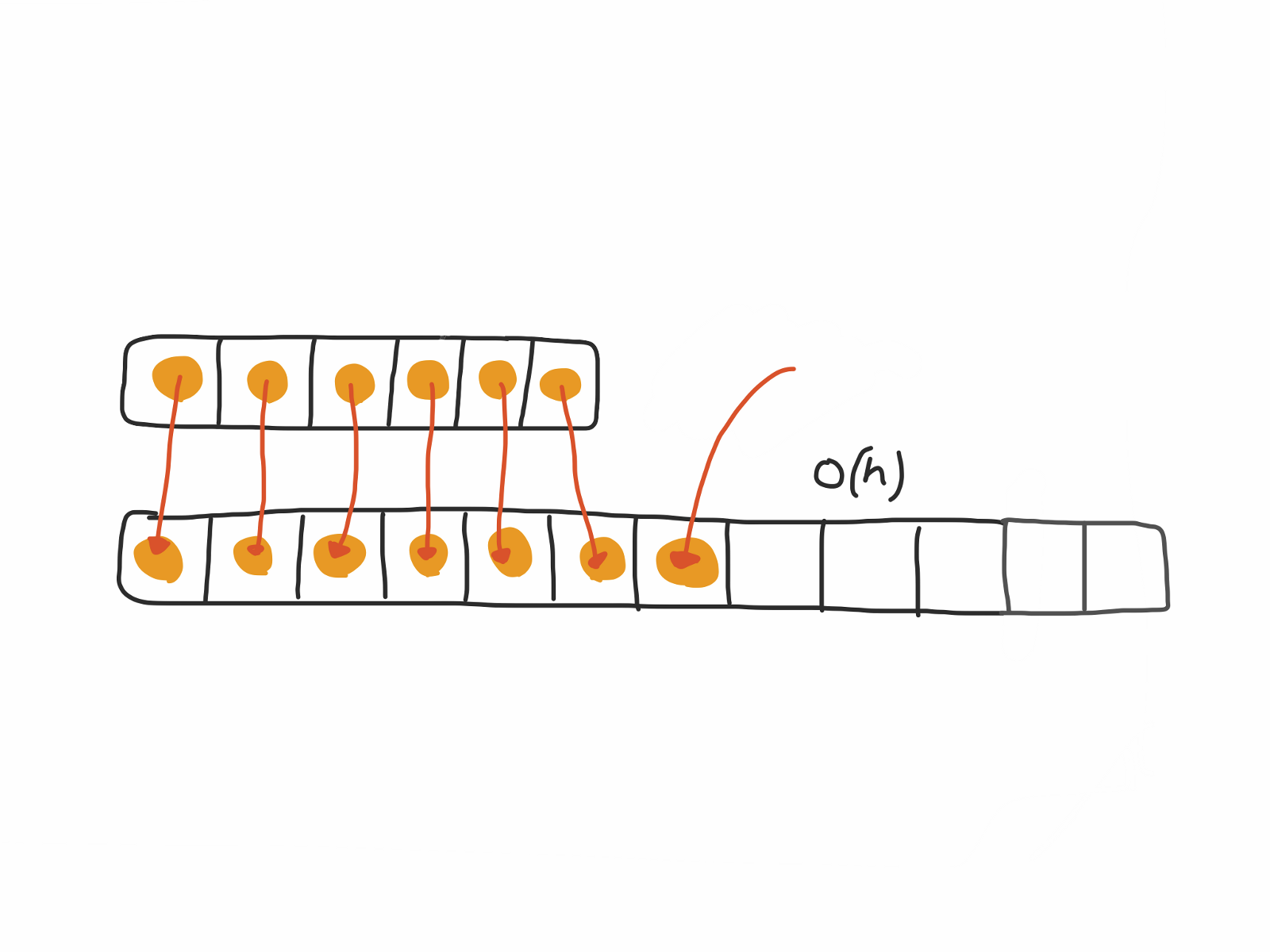
When the array in it has reached its capacity and need to re-create itself with the doubled size
The array has hit the capacity and we have no slots available. Then we need to create a brand new array with the doubled size. And then copy the items in the old one to the new one, which takes O(n) where n is the capacity of the old array and the worst case.
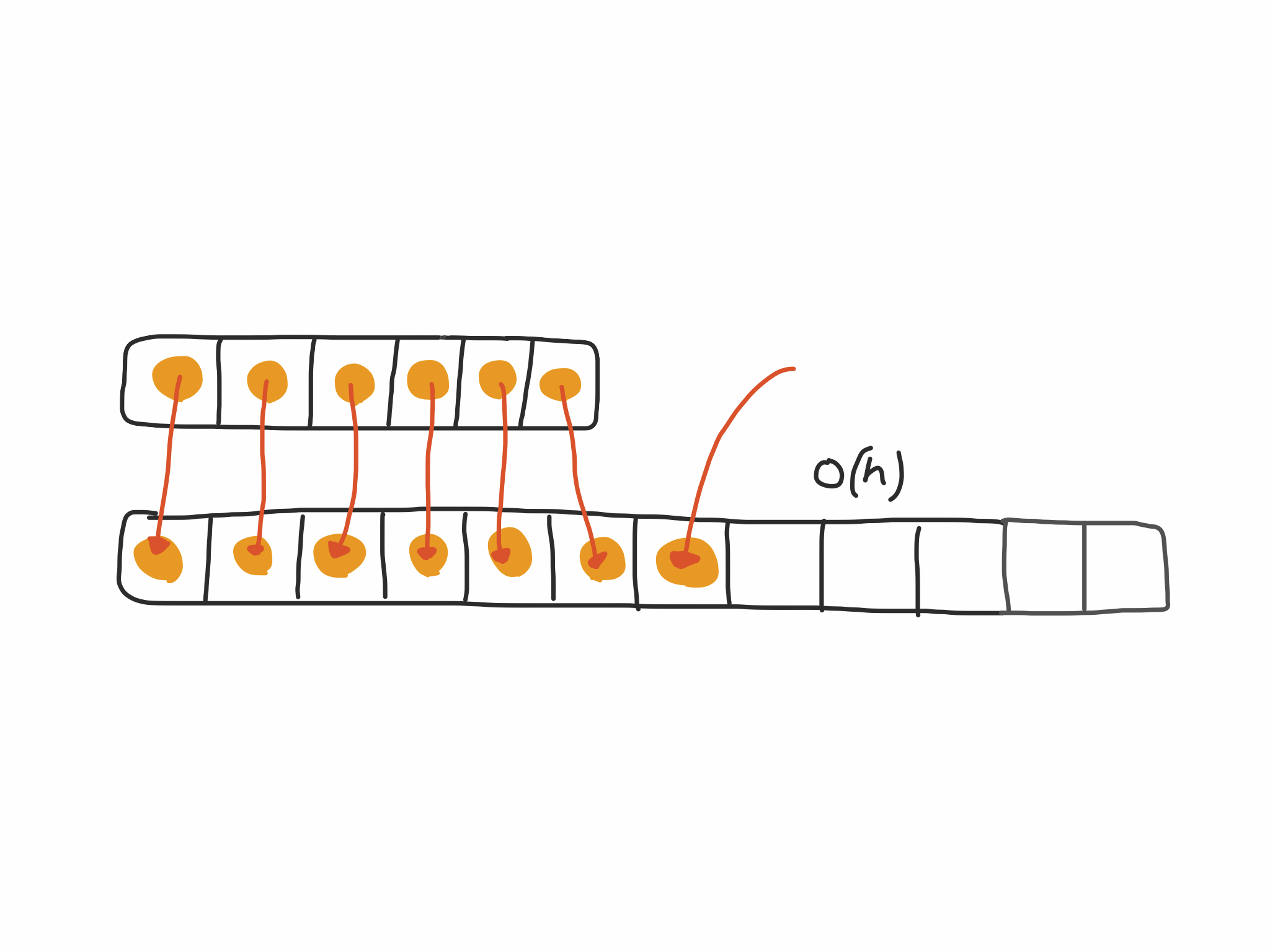
To express these two time complexity, amortized time is here. What it does is to let us describe the worst case happens once in a while every time the internal array hit its capacity.
But one it happens, it won?t happen again for so long that the cost is ?amortized.? (Cracking the Coding Interview 6th edition 43)
So how we describe the two complexities?
In the case of the ArrayList, we can say that
The insertion takes O(n) when the capacity has been reached, and the amortized time for each insertion is O(1).
But let?s be accurate for the worst time complexity without simplifying this time. If the internal array capacity starts with 1, then the capacities will be 1, 2, 4, 8, 16? X when it hits the capacity and gets doubled. It takes 1, 2, 4, 8 16? X items to copy into the new array depending on the capacity that has been reached. So the time complexity will be 1 + 2 + 4 + 8 + 16 +? X. If you think from X, this will be X + X/2 + X/4 + X/8? + 1 = 2X approximately. So in other words accurately,
The insertion takes O(2X) when the capacity of X has been reached, and the amortized time for each insertion is O(1).