How does recursion look in the call stack?
 Photo by Priscilla Du Preez on Unsplash
Photo by Priscilla Du Preez on Unsplash
With the widespread support of ECMA6 Script and ES2020 already coming over the horizon, Recursion, once often seen in JavaScript as a reference or a coding interview exercise example, is now becoming more common out in the wild.
Let?s look at some practical and effective examples of Recursion including:
- Defining recursion in JavaScript
- Call stack
- Iterative Vs. recursive solutions
- Pros and cons
What Is Recursion?
Recursion is a programming technique that solves complex problems by elegantly simplifying a repetitive execution into smaller executions of a similar nature.
Upon even closer examination, by leveraging the call stack in JavaScript, recursion winds up nested functions and then unwinds them. In many instances, implementing recursive solutions can help provide readability and reduce the time needed to debug code.
But let?s not get ahead of ourselves. To begin with, let?s first define recursion. Recursion is a function that calls itself.
For example, here?s some pseudo-code showing how recursion works:
function recursion() {return recursion()}recursion()
Notice that we are executing our recursion function twice, once within the scope of our function, and again outside in the global scope.
We execute the recursion function in the global scope first which then runs the recursion function script, which then calls the recursion function from within our recursion function. This, in turn, runs the function again, which again calls recursion ? adding recursion continuously to our call stack, thereby creating a loop.
With the code as it is, an infinite loop of nested functions is being added to the call stack.
The call stack is an area providing continuous memory which allows for local context and keeps track of multiple functions. The event loop then monitors the call stack and sends events or function callbacks whenever the call stack is empty.
If we were to run the recursion function above in the dev console we would receive the following error:

This brings us to how we set up a recursive pattern in a function.
By providing a base case to our recursive function, we can regulate the call stack of our nested functions. The base case is our condition which we can write that switches our call stack from being recursively wound to unwound.
Recursion Pattern Function
function recursionPattern(num) {// base caseif(num <= 0) {return 0 } else {// recursion executionreturn recursionPattern(num – 1)}}recursionPattern(5)
Our recursion will no longer exceed and break the call stack since we?ve supplied a base case: if(num <= 0). Now, once the argument num is less than or equal to zero, our function returns zero.
We further modified our recursion execution by calling the recursion function with its argument of numminus 1. The recursionPattern function will now always return zero and the call stack will no longer collapse.
Factorial Sums and Recursion
We dive deeper into the preliminaries of recursion with factorials and some algebra refreshers.
In programming, the factorial summation of a number is a number added by a number minus one, until the number reaches its conditional completion.
Observe the binomial coefficient formula below:
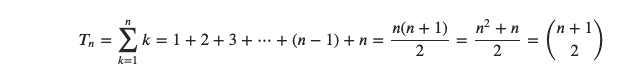
This might seem like a longish chain of numbers, but let?s not focus on every conversion. Instead, we can just grasp what we need from an extract of the simple formula: (n^n + n) / 2 .
Given this equation, let?s provide a practical context to our recursionPattern function above by slightly modifying the function to solve factorials with summation.
We can do this by simply returning our function?s argument num + our recursion execution with the argument of num ? 1:
function factorialSum(num) {if(num <= 0) {return 0 } else {return num + factorialSum(num – 1)}}factorialSum(5)// returns 15
Let?s break down the recursion pattern execution in our function above.
First off, our function takes an argument num.We then set up our base case, which is the conditional if code block. if(num <= 0) {return 0 .
If our argument is less than or equal to zero we return 0 and end, adding a new nested function to the call stack.
Our else statement executes the factorial summation equation by concatenating our num (argument) to our recursion execution factorialSum(num ? 1. We subtract 1 from our argument in our function call so that each time we call the function again our num argument loses a value of 1.
The call stack winds up starting at 5 ? the initial argument: factorialSum(5). Then JavaScript will add 5 in memory to the call stack and subtract 1 from our argument so our new argument number is now 4. Following that, ot will add 4 in memory to the call stack and execute the function again. Our new argument is now 3. This continues until we reach our base case, 0.

Once we reach our base case the call stack has wound up all the recursive nested functions which it then returns in the first order (the last function called) back to the last function (the first function called).
This may seem counter-intuitive at first. However, in the following examples we?ll break this down and view it more clearly.
Iterative Solution Vs. Recursive Solution
For every recursive solution out there, there is an equal iterative solution. In that sense, recursion acts as a looping mechanism unto itself and leverages the call stack to complete its task. An iterative solution to the same problem relies on iterative looping constructs.
For example, if we are asked in a coding challenge or interview question to find the recursive solution, a technique to do so would be to first write out the iterative solution and then use that to map out the recursive one.
Let?s examine the following problem and write out an iterative solution followed by a recursive solution. By going through the process we can examine how this all works.
Iterative Solution Example
Take a look at the following code:
In the example above, we see a function which takes two arguments, startValand endVal. As the names suggest, the startVal is the starting number of an array argument, and the endVal is the end number of the array.
The aim of the function is that by providing these two arguments when calling the function, we return an array of all the numbers in sequential order between the startVal and the endVal.
Therefore, if our starting number startVal is 1 and our ending number endVal is 5, the function would return: [1,2,3,4,5]
Let?s examine how this works in our iterative solution above. First, we create an empty array. Then we set up our for…loop with three conditions. We initialize i (index) to our startVal the starting number. We then set up our loop with set the i (index) to run until we reach the endVal.
Our final condition is to add one after every run through to i. Finally, we push the results into our array arr.push(i). It’s all pretty logical and well laid out.
Now that we?ve gone through an iterative solution to creating an inclusive array between two numbers, let?s build a recursive solution following the similar fundamental logic of the looping pattern, but applied to the call stack rather than the looping construct.
Recursive Solution Comparison
First, let?s create the function with the same two arguments:
function inclusiveArrayParamRecursive(startVal, endVal) {}
Next, we create a base case that follows the similar logic condition we applied to our for?loop conditions.
In the for?loop from our previous function we wrote:
for(let i = startVal; i <= endVal; i++)
We set i to the startVal and then we run the loop of i which is now the startVal until it is less than or equal to the endVal.
For our base case in the recursive solution we can apply a similar approach. By setting an if else conditional block, so that once startVal is greater than or equal to the endVal, we return the start value and end our recursion. Otherwise, we run the recursion execution.
Our inclusiveArrayParamRecursive now looks like this:
if(startVal >= endVal) {return [startVal]} else {}}
We can then simply create a variable and set it to our recursion execution with our start value and our end value subtracted by one to create the wind end point in the call stack. In the new variable, we push the results of each endVal into the array and then the call stack returns all the nested functions once we hit the base case.
Our final recursion solution is as follows:
Although we?re subtracting one from each endVal and are starting at our endVal argument of 6, pushing each new endVal into the array, we receive an incremental order starting at 2 our startVal.
This may have seemed counterintuitive, but hopefully, noting how the call stack now works, this now makes more sense. The call stack winds up the numbers and stores the nested functions and then returns them once the base case is met. Hence, we receive an incremental array and not decremented.
Conclusion
Now that we?ve gone over iteration vs. recursion, a good exercise would be to create a recursive function that produces an incremental array beginning at 0 to n. Start by writing the iterative solution and then move on to the recursive one.
By breaking down and observing practical examples of recursion and how they?re formed as effective solutions to more common JavaScript problems, we can provide a better context as to how the pattern of recursion can be a beneficial implementation to our programming.
Although recursion can help improve time complexity and clarity of code, as well as making for better debugging for code, it?s important also to be wary of its shortcomings. These include the fact that it uses up more memory and would also be slower than certain iterative solutions.
Many web developers who have been working in the industry for at least a few years would agree that JavaScript has gone through quite the evolution in the past decade.
Keeping an eye and overview on the implementation progress and patterns of recursion in JavaScript is a great way of seeing how and where the language is today and where it?s going in the future.
That?s it. Thanks for reading along and I hope that you have found some of this useful.
Please find a full video tutorial on recursion below, a repository of Recursive Vs. Iterative Solutions to add to or check out, and some other resources below.
Video tutorial
Source code