We have covered projection in Dot Product. Now, we will take deep dive into projections and projection matrix.
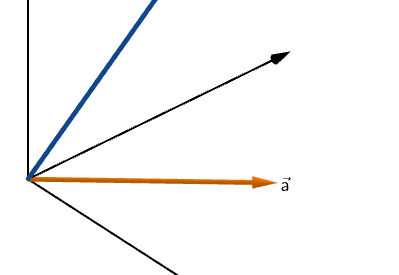
Consider two vectors in 3D vector space: a and b
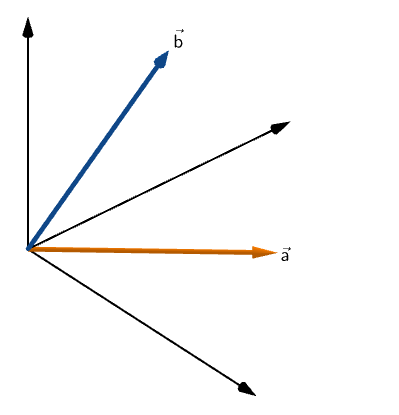
Say, we have a point R on vector a that is closest to vector b
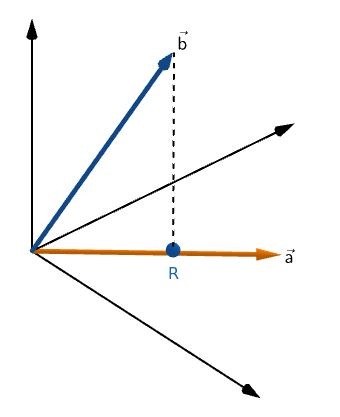
We can construct a vector to the point R having the same direction as vector a.
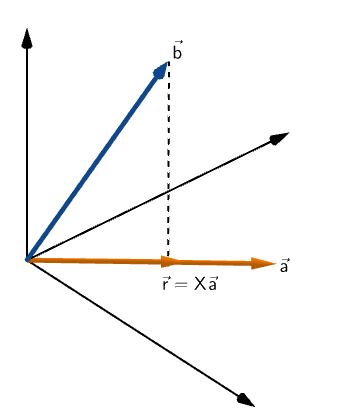
As the new vector r shares the direction with vector a, it could be represented as a product of vector a with some scalar quantity (in this case, X).
Assuming the distance between point R and vector b is (b-r).
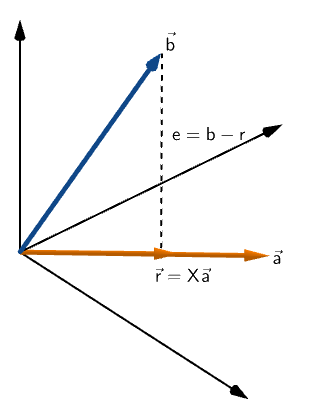
From the figure, we can see that e is perpendicular to a.
So
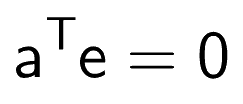See orthogonal vectors
This equation could be simplified further for the value of X
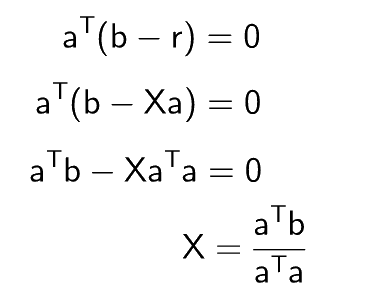
We know that
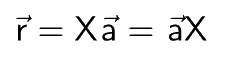Scalar multiplication is commutative
Now we will simplify this equation
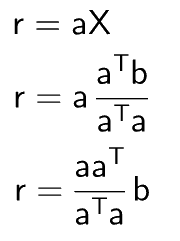
Coming back to the figure
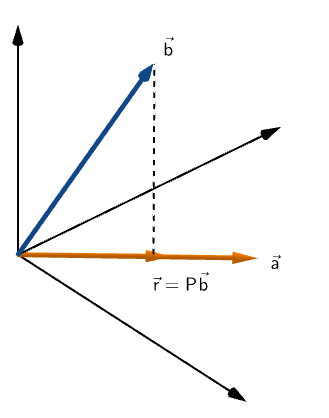
If vector r is a projection of vector b on vector a.
Then vector r could be represented as
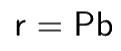P is Projection matrix
and
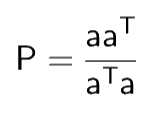
Properties of Projection Matrix
The projection matrix has some amazing properties like
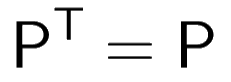Projection matrix is symmetric
and
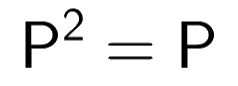Square of projection matrix is itself
The matrices that having this property are called Idempotent Matrices.
So, if we project a vector twice the result will be same as with projecting once.
Why use projections?
Suppose we have a matrix A comprising of two column vectors a1 and a2.
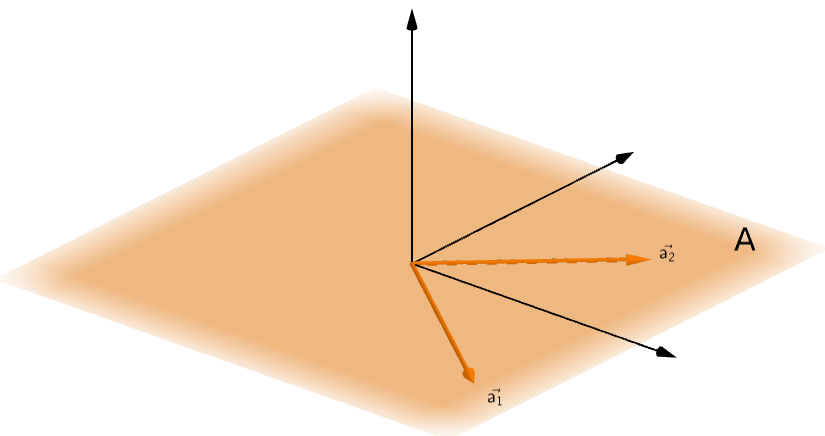Column Space of A
Now, we have to find solution of
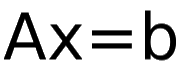
such that vector b does not lie in column space of matrix A.
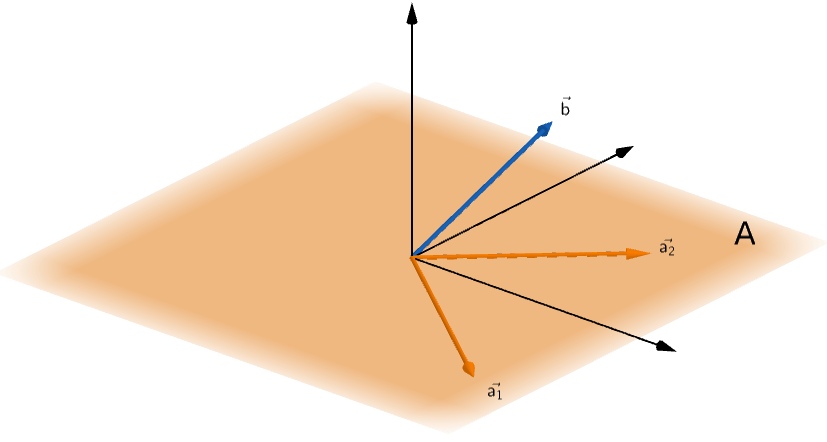Vector b lies outside the column space of A
Looks like there are no solutions to this equation because there is no way vector b could be represented as a linear combination of a1 and a2.
But, if we project vector b onto the column space of A
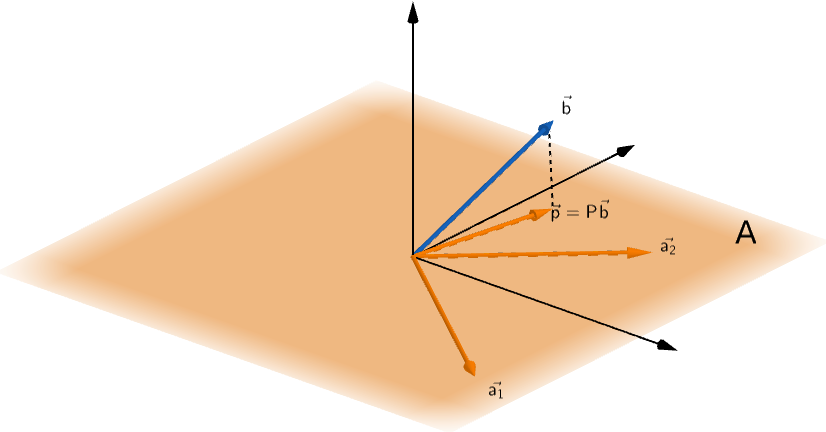Vector p is projection of vector b on the column space of matrix A
Vectors p, a1 and a2 all lie in the same vector space.
Therefore, vector p could be represented as a linear combination of vectors a1 and a2.
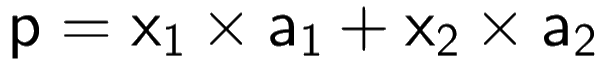x1 and x2 are the coefficients to be multiplied with vectors
This could be broken down in the form of matrices
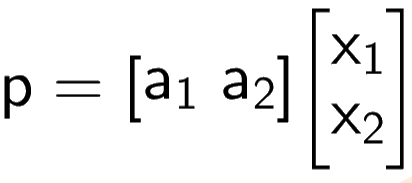
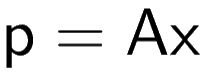
We can solve for matrix x and we may get a solution to the problem we previously thought was unsolvable.
Read Part 18 : Norms
You can view the complete series here
Connect with me on LinkedIn.
