Optimization (finding the maxima and minima) is a common economic question, and Lagrange Multiplier is commonly applied in the identification of optimal situations or conditions. Even though it is straightforward to apply it, but it is NOT intuitively easy to understand why Lagrange Multiplier can help find the optimal. Let?s try to explain in the following and demonstrate by examples.
First, it is taught in high school (or 1st year in university curriculum) that putting the first derivative of a function to zero (finding the coordinates of a function such that the slope at the tangent point is zero) is the condition of the maxima or minima. For example, for the function of y=ax+bx+c, if we put dy/dx=2ax+b=0, then [x=-b/2a, y=a(-b/2a)+b(-b/2a)+c] is the max/min point such that the tangent slope is zero. For details, readers may refer any introduction to calculus pages, say https://www.mathsisfun.com/calculus/maxima-minima.html
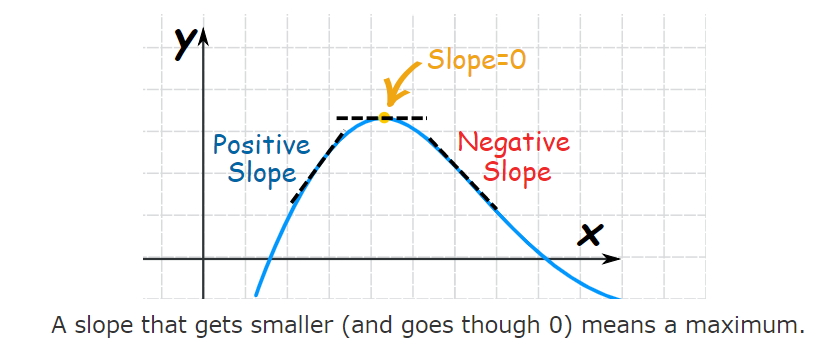Figure 1 Optimization by putting the first derivative to zero. Source: https://www.mathsisfun.com/calculus/maxima-minima.html
However, many economic questions are looking for the optimal under constraints, instead of the absolute maxima/minima. Thus, Lagrange Multiplier is developed to figure out the maxima/minima of an objective function f, under a constraint function g. It can be understood more easily graphically.
- Graphical interpretation of Lagrange Multipliers
Graphically, Lagrange Multipliers are for finding the max and min coordinates of the tangent points between the objective function f(x,y) and the constraint function g(x,y)-c
For example, if f(x,y): = 2x+y, and g(x,y)-c: x+y-1, then the Lagrange Multiplier is
Z=2x+y+L(x+y-1)
put dZ/dx=0, dZ/dy=0, dZ/dL=0
then 2+2Lx=0, 1+2Ly=0, x+y=1
x=-1/L, y=-1/2L, 1/L+1/(4L)=1
L=(5/4)?.?, x=-(4/5)?.?, y=-(1/2)(4/5)?.?
graphically these 2 points are the tangent points of the unit circle g and the 2 straight line f. Intuitively, the Lagrange Multiplier shifts the objective function f until it tangents the constraint function g, the tangent points are the optimal points.
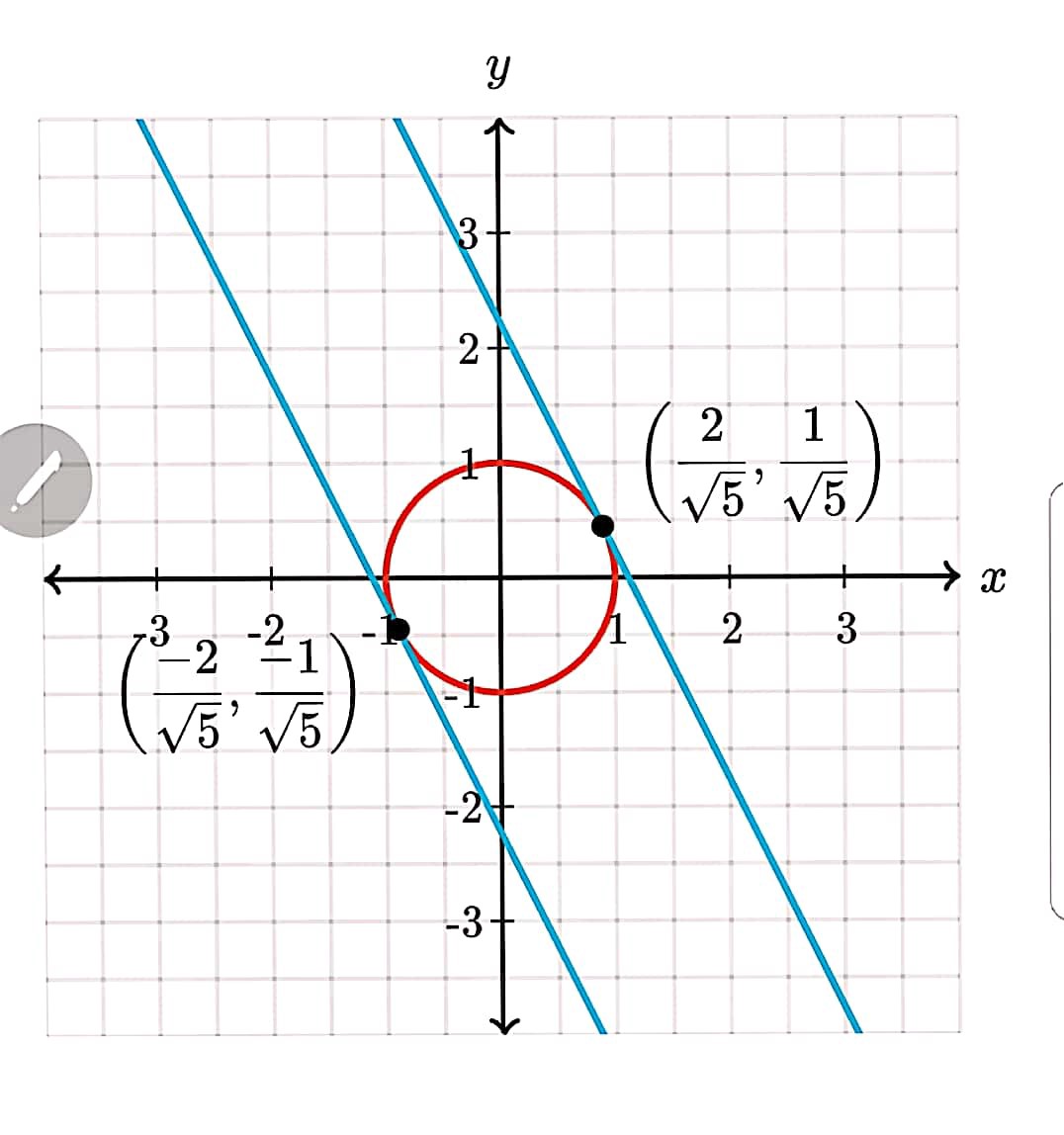Figure 2 An example of applying Lagrange Multiplier to find the optimal
for more details, see https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/constrained-optimization/a/lagrange-multipliers-single-constraint
2. Solving a production maximization problem by Lagrange Multipliers
There are a lot of practical applications of applying Lagrange Multipliers, such as optimizing production size in Managerial Economics as follows:
For example, if the total cost of the production of a good is C = 10l + 40k
where l is labor input in hours, and k is capital input in hours. If labor cost per hour is $10, and capital cost per hour is $40.
Now for an order of producing 1000 units, the constraint fn is Q=20(l?.?k?.?)
Then the Lagrange Multiplier is
Z=10l+40k + L(20l?.?k?.??1000)
put dZ/dl=0, dZ/dk=0, dZ/dL=0,
L=2, l=100, k=25
i.e. the optimal is to involve 100 hours labor and 25 hours capital to produce the 1000 units
for details, see https://www.dummies.com/education/economics/how-to-use-the-langrangian-function-in-managerial-economics/
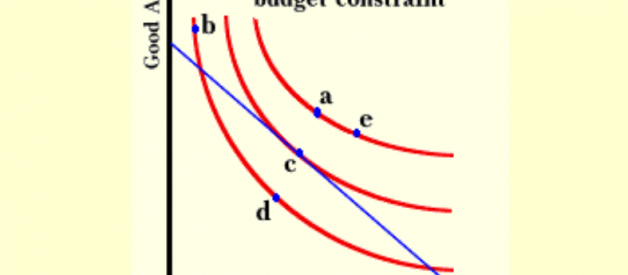
3. It is a very common and basic economic question of identifying the maxima of consumption in consumers? indifference curves under the constraint of the budget line. Let?s demonstrate it by finding the tangent point of the budget line (say g=x+y-c) to the outermost indifference curve (say f=xy).
In case you would like to review the background information of Budget Line and Indifference Curves, you may refer to the youtube https://youtu.be/MXIgp-P-FeY first.
In other words, we are going to maximize the objective fn, f=xy
subject to the constraint fn, g=x+y-c
The Lagrange Fn is
Z: xy + L(x+y-c)
put dZ/dx = y+L = 0
put dZ/dy = x+L = 0
put dZ/dL = x+y-c = 0
thus L = -c/2, x=y= -L
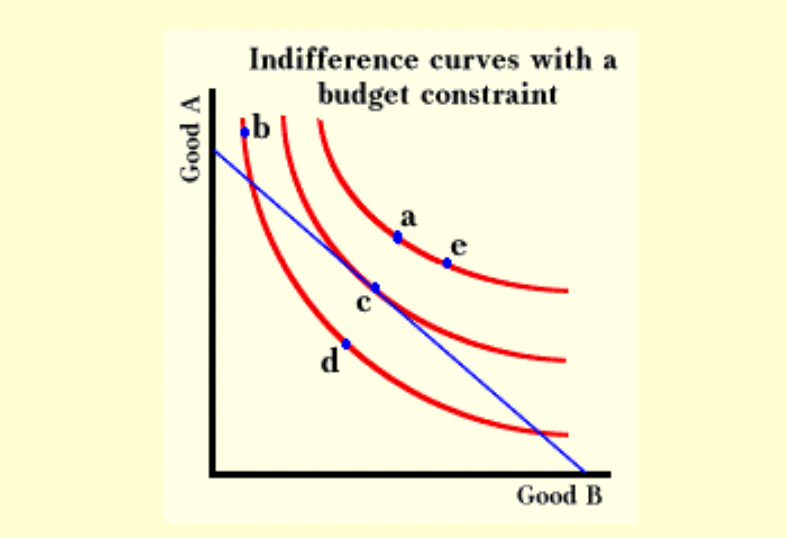Figure 3 The Maxima of Consumers? Consumption at the Indifference Curves subject to the Budget Constraint
Intuitively, the Lagrange Multiplier shifts the indifference curves (like contour lines) such that it tangent the Budget Line, and the tangent point is the maxima.
For example, if c = 12, then x=y=6, L=-6
see https://youtu.be/H4HN4ZrVm0w
