Logistic regression and support vector machines are supervised machine learning algorithms. They are both used to solve classification problems (sorting data into categories). It can be sometimes confusing knowing when to use either of these machine learning algorithms, I am going to provide guidelines on which to use depending on the amount of data or features that you have.
Logistic Regression
Logistic regression is an algorithm that is used in solving classification problems. It is a predictive analysis that describes data and explains the relationship between variables. Logistic regression is applied to an input variable (X) where the output variable (y) is a discrete value which ranges between 1 (yes) and 0 (no).
![]()
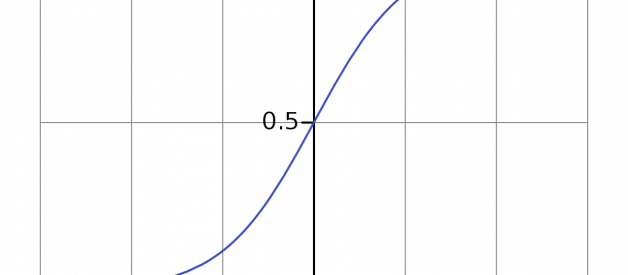
It uses logistic (sigmoid) function to find the relationship between variables. The sigmoid function is an S-shaped curve that can take any real-valued number and map it to a value between 0 and 1, but never exactly at those limits.
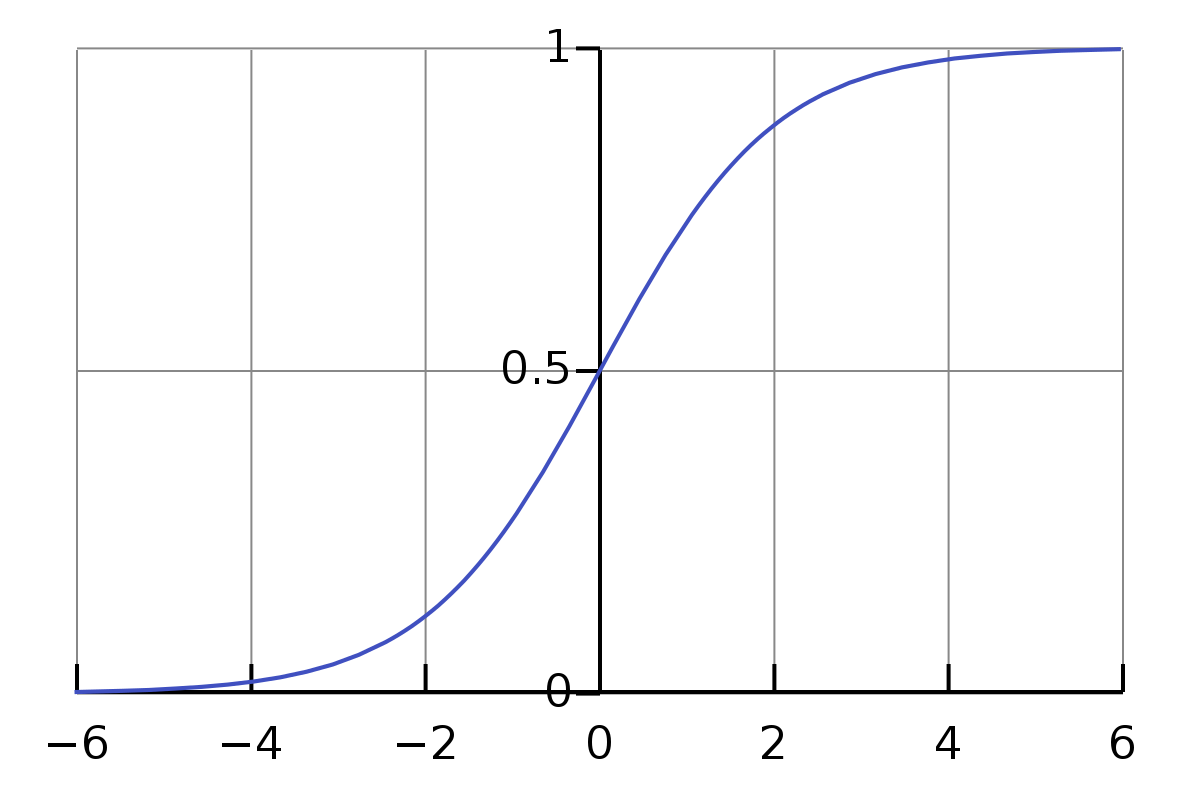 Illustration of a Sigmoid Curve from wikipedia
Illustration of a Sigmoid Curve from wikipedia
Problems to apply logistic regression algorithm
- Cancer detection ? can be used to detect if a patient have cancer (1) or not(0).
- Test score ? predict if a student passed(1) or failed(0) a test.
- Marketing ? predict if a customer will purchase a product(1) or not(0).
Here is a very detailed overview about logistic regression algorithm.
Support Vector Machine
The support vector machine is a model used for both classification and regression problems though it is mostly used to solve classification problems. The algorithm creates a hyperplane or line(decision boundary) which separates data into classes. It uses the kernel trick to find the best line separator (decision boundary that has same distance from the boundary point of both classes). It is a clear and more powerful way of learning complex non linear functions.
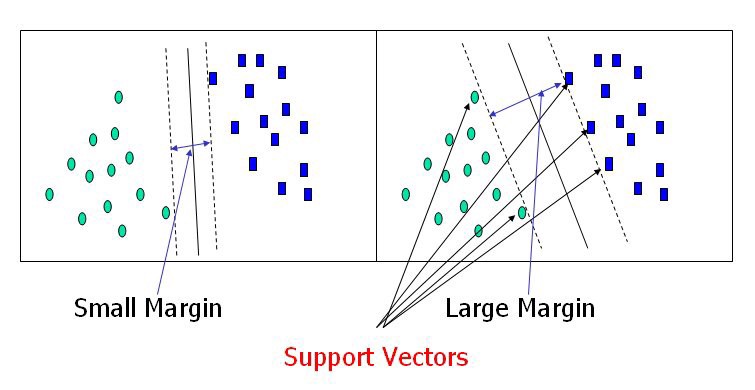
Here is a very detailed overview about support vector machine algorithm.
Problems that can be solved using SVM
- Image classification
- Recognizing handwriting
- Caner detection
Difference between SVM and Logistic Regression
- SVM tries to finds the ?best? margin (distance between the line and the support vectors) that separates the classes and this reduces the risk of error on the data, while logistic regression does not, instead it can have different decision boundaries with different weights that are near the optimal point.
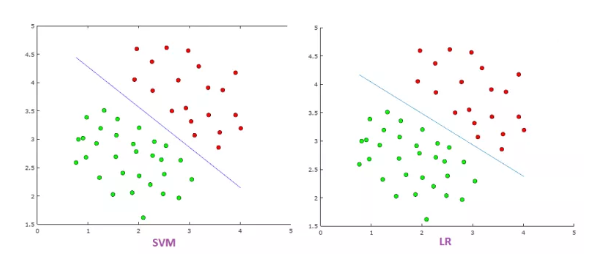
- SVM works well with unstructured and semi-structured data like text and images while logistic regression works with already identified independent variables.
- SVM is based on geometrical properties of the data while logistic regression is based on statistical approaches.
- The risk of overfitting is less in SVM, while Logistic regression is vulnerable to overfitting.
When To Use Logistic Regression vs Support Vector Machine
Depending on the number of training sets (data)/features that you have, you can choose to use either logistic regression or support vector machine.
Lets take these as an example where :n = number of features, m = number of training examples
1. If n is large (1?10,000) and m is small (10?1000) : use logistic regression or SVM with a linear kernel.
2. If n is small (1?10 00) and m is intermediate (10?10,000) : use SVM with (Gaussian, polynomial etc) kernel
3. If n is small (1?10 00), m is large (50,000?1,000,000+): first, manually add more features and then use logistic regression or SVM with a linear kernel
Generally, it is usually advisable to first try to use logistic regression to see how the model does, if it fails then you can try using SVM without a kernel (is otherwise known as SVM with a linear kernel). Logistic regression and SVM with a linear kernel have similar performance but depending on your features, one may be more efficient than the other.
Logistic regression and SVM are great tools for training classification and regression problems. It is good to know when to use either of them so as to save computational cost and time.