The daily fantasy sports (DFS) industry is booming. Market leaders DraftKings and Fanduel generate millions of dollars in annual revenue from entry fees for their daily sports contests, where users hand-pick lineups of real athletes and win money based on their players? statistical performance.
Each year at ASICS Digital, a group of employees form a DraftKings league during football season to compete with one another and earn bragging rights in the office. I?ve always enjoyed the challenge of drafting the perfect team and the competitive banter with my coworkers. This year, I decided to mix things up a bit and try to use my engineering background to my advantage.
While football itself is an exhibition of physical power and pinpoint coordination, the game of fantasy is all about the numbers. My vision was to leverage my knowledge of algorithms and optimization methods to help me build the perfect DraftKings football lineup each week.
Was this possible? Did it make me a millionaire? And furthermore, what lessons did it teach me about software engineering in general?
What is DFS?
To start, we need to understand the basic mechanics of the game. In our case, we?re focusing specifically on daily fantasy football. Each week, users ?draft? a roster of NFL players, attempting to maximize their potential to score fantasy points while staying under a $50,000 salary cap. Salaries are assigned to individual players by DraftKings each week based on their expected performance. The composition of your roster is also constrained by DraftKings, with most contests requiring one quarterback, two running backs, three wide receivers, one tight end, one team defense, and one ?flex? position (this can be filled by either a running back, wide receiver, or tight end). In order to enter a contest, the user pays an entry fee, and at the end of the week, prize money is paid out to the top-scoring teams.
There are many ways to approach building a lineup. Some users choose players from their favorite NFL teams, while others attempt to ?stack? multiple players from a single game that is expected to be a high-scoring affair. To me, these pseudo-strategies seemed too subjective and inconsistent to rely on for a programmatic solution. I recognized a pattern in DraftKings? contest model that I?d seen before in one of my college computer science classes: a combinatorial optimization classic known as the knapsack problem.
The Knapsack Problem
Let?s imagine a hypothetical scenario to better understand this problem. Consider yourself living in a world on the brink of a zombie apocalypse. You need to flee your apartment in the city and head for the countryside to hunker down and weather the outbreak. All you have is a single knapsack to fill with your most treasured belongings, and the knapsack can only carry 50 lbs of items. How do you choose which of your belongings to include in the knapsack to maximize the value while staying under the 50 lb weight constraint?
 Good thing he?s wearing ASICS?
Good thing he?s wearing ASICS?
The problem doesn?t sound particularly complex at first, but in reality, it?s much more difficult than it seems. The knapsack problem is considered to be NP-complete, meaning there is no known polynomial-time algorithm that can solve it. In this context, polynomial-time refers to the time complexity of the problem. Time complexity is a way to measure approximately how long an algorithm could take to run in the worst-case scenario given different numbers of inputs. If we measure the complexity of an algorithm as a function of n, where n represents the number of inputs, we can approximate how long it will take to solve different instances of the problem. Time complexity is commonly represented using big O notation, where O(n) would represent an algorithm which could require n simple operations to solve given n inputs.
For example, take a simple task such as counting the number of marbles in a jar. If we assume that it takes you 1 second to count a single marble, we can determine that the complexity of counting n items is linear, or O(n). This means that the amount of time needed to solve the problem increases uniformly to the number of inputs. Counting 5 marbles would take 5 seconds, counting 20 marbles would take 20 seconds, counting 100 marbles would take 100 seconds, and so on.
Consider another example, like sorting the elements of a list. A simple sorting algorithm such as insertion sort has quadratic time complexity, or O(n). This means that instead of requiring one operation per input, like the counting example, it could require up to n operations per input. If we again assume an arbitrary unit size of 1 second per operation, sorting a list of 5 items would take 25 seconds, sorting a list of 20 items would take 4,000 seconds (1 hour, 6 minutes), and sorting a list of 100 items would take 10,000 seconds (2 hours, 46 minutes). It is immediately clear that with greater orders of complexity, the amount of time required for large-input problems is daunting.
But for our use case, the dreaded knapsack problem, we?re in even bigger trouble. The most simple version of the problem assumes a set of n items of varying weight and value, each of which can only be included once in the knapsack. The only known solution to this problem that is 100% correct is to try every possible combination of items that will fit in the knapsack. This brute-force strategy has exponential complexity, or O(2?). To put it in perspective, assuming the 1 second operation time again, solving for a set of 5 items would take 32 seconds, solving for 20 items would take 12 days, and solving for a set of 100 items would take 40 billion billion millennia.
Yep, you read that right. Even if you ran the algorithm at that rate for the entire lifespan of our universe (~13.7 billion years), and then did that again a billion more times, you?d only be 0.03% finished.
 Approximate worst-case time to run algorithm assuming 1 second per elementary task
Approximate worst-case time to run algorithm assuming 1 second per elementary task
Needless to say, this presents quite the dilemma. A brute-force approach clearly isn?t feasible for larger data sets, so I knew I would need to employ some additional strategies to make this work. Thankfully, I had some experience with optimization methods, so I rolled up my sleeves and dug in?
The Optimizer
I decided to build an iOS app as a lightweight front-end for my optimizer. The app needed to handle two basic tasks:
- Download player data for the current week
- Find optimal lineups by solving the knapsack problem
OK, so maybe task 2 isn?t ?basic,? but whatever. We?ll get to that.
As for task 1, I was relieved to discover that FantasyPros posts salary data for DFS platforms on their website each week. Using the SwiftSoup library, I was able to quickly throw together some code to scrape their HTML tables and download the salary data. This handled the weight component of the knapsack problem.
The knapsack problem also states that each item must have a value associated to it. In our case, this part is a bit unconventional. DraftKings lineups earn points based on players? statistical performance in games, but at the time of drafting the lineups, we don?t know the results of these games yet. Unsurprisingly, though, there is a great deal of demand for these sorts of predictions in the fantasy sports community. Websites such as ESPN and CBS Sports have experts who publish weekly fantasy point projections for NFL players. I was again relieved to discover that FantasyPros aggregates and posts these projections each week, in addition to their salary data. I whipped up some more sloppy SwiftSoup code to scrape this webpage, and voila! I had an intact set of n items (players) with weight w (salary) and value v (projected points), just as the knapsack problem requires.
Now for the hard part. As we mentioned previously, brute-force algorithms perform horribly for problems with exponential complexity and a large number of inputs. The 9-player DraftKings lineup is a slightly different take on the classic knapsack problem, as it defines positional constraints as well. This will actually help us out a bit, as it limits the number of possible configurations. But even if we only consider one player from each NFL team per position, the number of possible lineups is still pretty mind-boggling. Let?s assume we?re playing a wide receiver in our flex slot for simplicity?s sake and crunch the numbers:
C(n, r) represents the number of ways to choose r elements from a group of size n.QB: C(32, 1) = 32RB: C(32, 2) = 496WR: C(32, 4) = 35,960TE: C(32, 1) = 32FLEX: C(89, 1) = 89DST: C(32, 1) = 3232 * 496 * 35,960 * 32 * 89 * 32 = 52 trillion lineups
Alright, 52 trillion is a lot of lineups. But that number is a bit more tangible than our 40 billion billion millennia example from before. The other good news is that the hypothetical one-second-per-operation rate is much slower performance than we can expect from any modern computer. It?s more realistic to assume that our optimizer can perform thousands ? if not millions ? of operations per second, which will also help out.
But in reality, we need to consider more than one player from each team. A safer assumption might be that each NFL team has 1 quarterback, 2 running backs, 3 wide receivers, and 2 tight ends who will be statistically relevant in fantasy sports based on their involvement in the game. Plugging those numbers into our most recent example yields depressing results:
QB: C(32, 1) = 32RB: C(64, 2) = 2,016WR: C(96, 4) = 3,321,960TE: C(64, 1) = 64FLEX: C(217, 1) = 217DST: C(32, 1) = 3232 * 2016 * 3,321,960 * 64 * 217 * 32 = 95 quadrillion lineups
Well, we?re moving in the wrong direction. Let?s assume we can perform 1 million elementary operations per second (probably optimistic):
95 quadrillion lineups / 1 million lineups per second = 95 billion seconds = 3,020 years
Ugh. Alright, by now we get the point. Math is stupid and 3,000 years is a long time. What are we gonna do about it?
One way to approach NP-complete problems like the knapsack problem is to use a heuristic algorithm. A heuristic algorithm is basically a shortcut: a solution that sacrifices accuracy or completeness in favor of speed. I decided to use a variation of a greedy algorithm for my optimizer, which basically makes the optimal local decision at each step in the process, without necessarily thinking about the long-term or holistic outcome.
For my greedy approach, I decided to rank players based on their value-to-weight ratio (v/w). Since our goal is to optimize value given constraints on weight, this seemed like a good, greedy way to prioritize our picks. If we only consider the top 10 players for each position when sorting by value-to-weight ratio, we should be able to significantly limit the number of necessary iterations:
QB: C(10, 1) = 10RB: C(10, 2) = 45WR: C(10, 4) = 210TE: C(10, 1) = 10FLEX: C(23, 1) = 23DST: C(10, 1) = 1010 * 45 * 210 * 10 * 23 * 10 = 217 million lineups
Progress! Assuming our same 1 million operation per second rate:
217 million lineups / 1 million lineups per second = 217 seconds = 3 min, 36 sec
That?s a reasonable amount of time, but it still feels a little bloated. Instead of exhausting every possible outcome, why don?t we just set a cap on the number of combinations? We?re already using a greedy algorithm, so it seems possible that we reach an optimal or near-optimal solution early on in the process.
I ended up implementing a slider that allows the user to specify how many iterations to attempt before displaying the results. This allows the user to control how much time the optimizer runs for and also lets us get an idea of the benefit of running the more exhaustive searches. I ultimately decided on a range of 1 million to 10 million iterations, which usually takes about 5 seconds and 50 seconds to run, respectively. The combinations are generated randomly to prevent getting buried too far down a single decision tree.
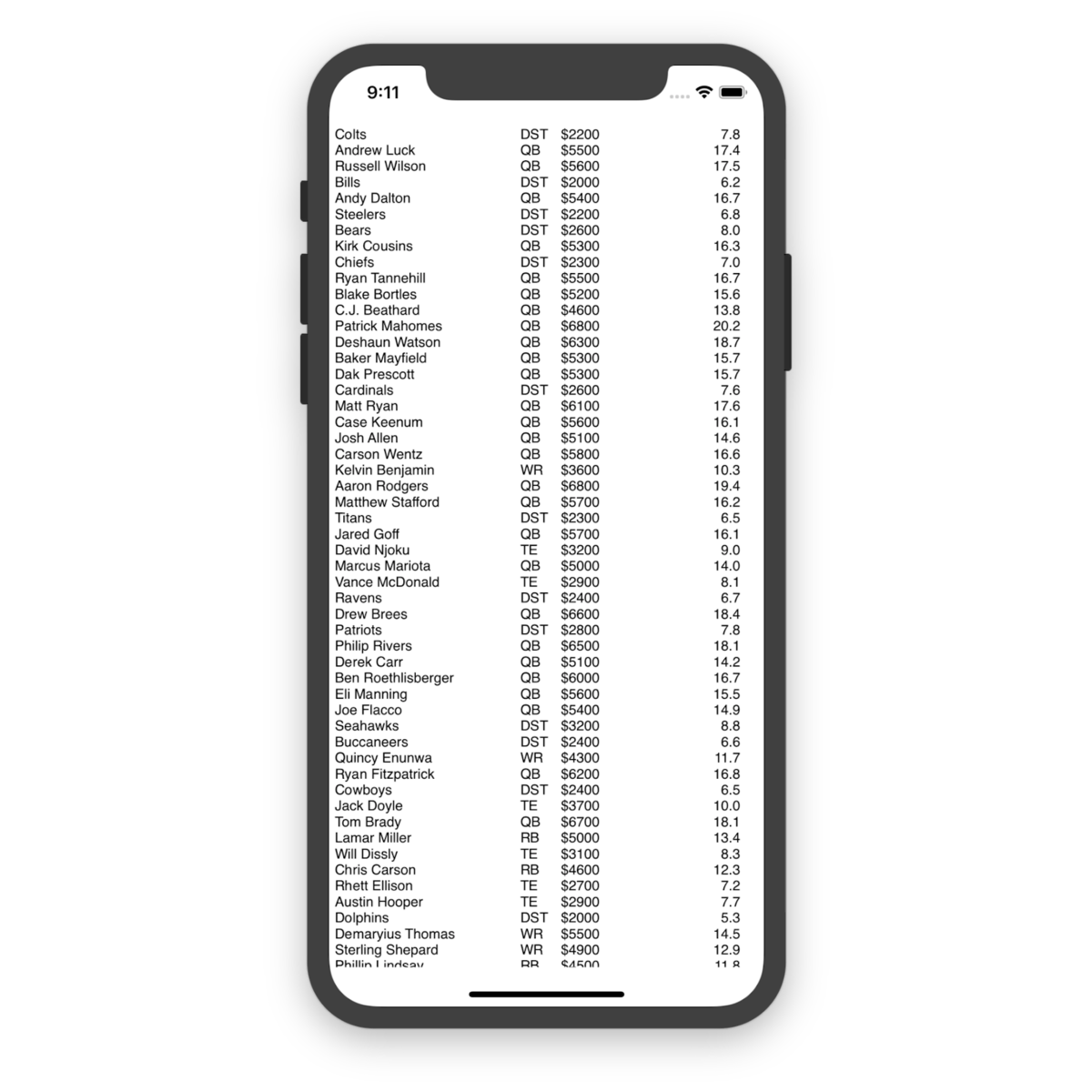
Running the app for 1 million iterations on an iOS simulator on my MacBook only took 4.18 seconds to complete and found some pretty high-scoring lineups. The #1 lineup found used all $50,000 of the salary cap and had a projected point total of 135.8 points.
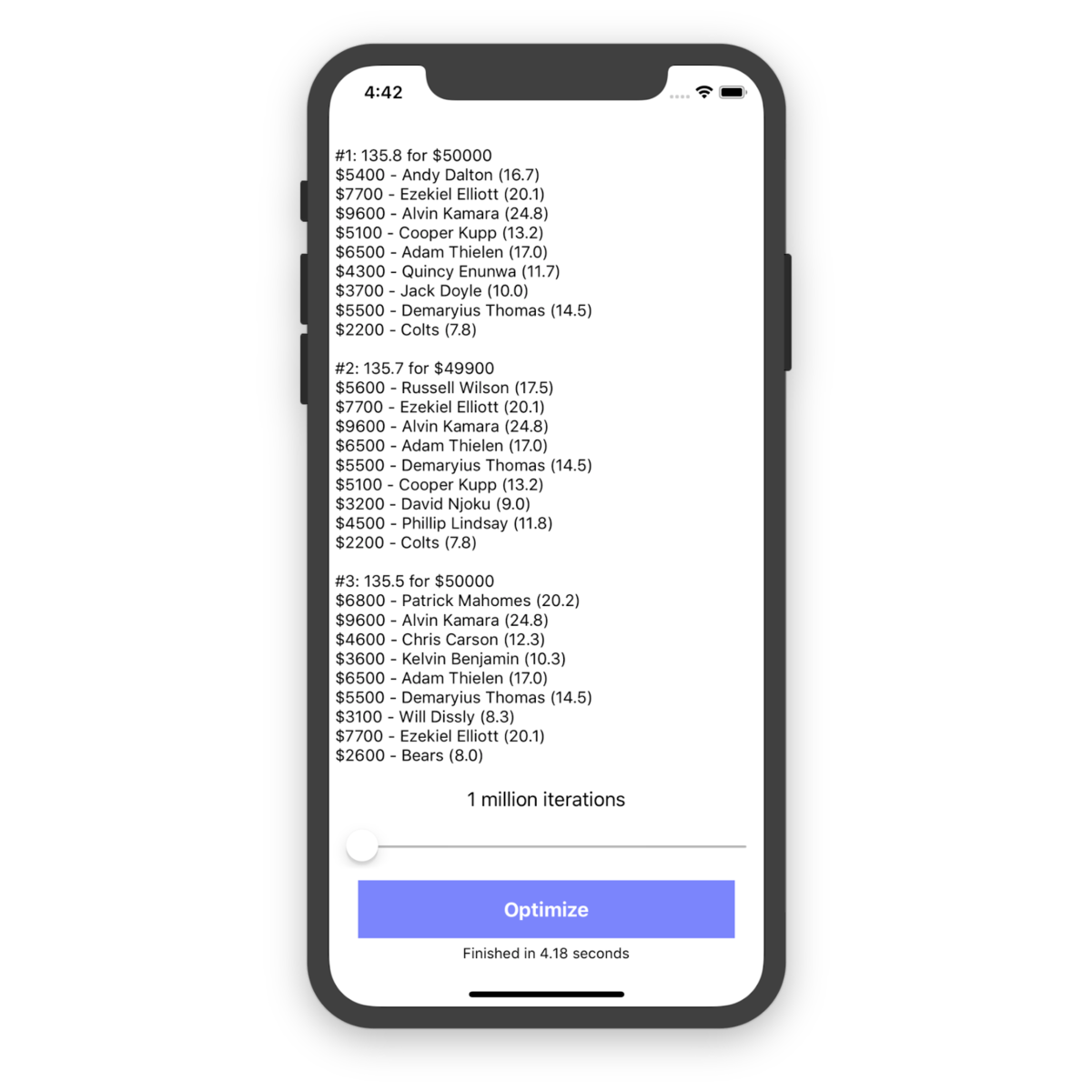
Next, I ran the optimizer for the maximum 10 million iterations to compare results.
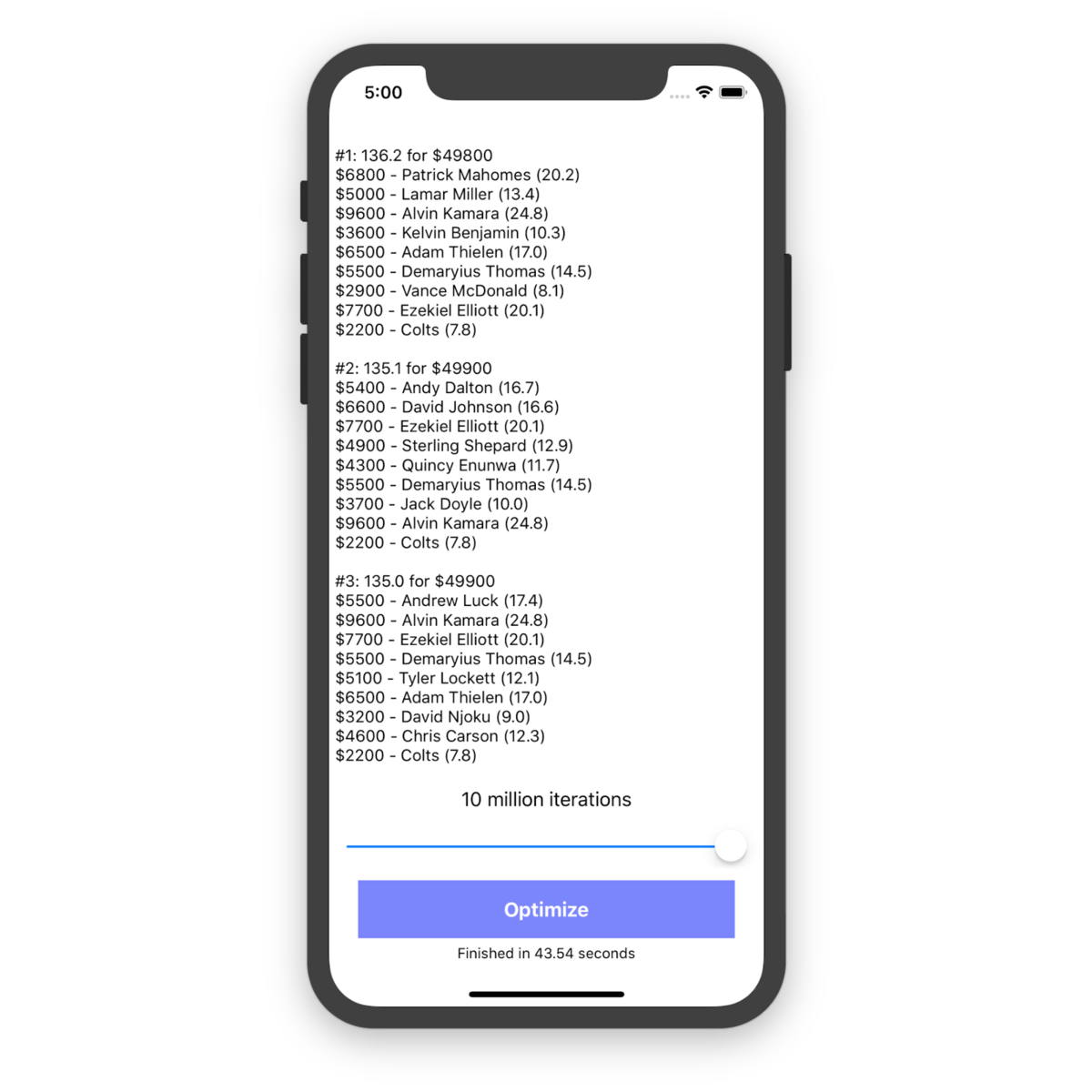
This time it found a lineup projected for 136.2 points with $200 to spare. I went on to run the optimizer dozens of times over the course of the week, and began to realize that these results were pretty close to optimal. With this set of projections and salaries, 136.2 seemed to be the greatest point total possible. Since the knapsack problem is NP-complete, it?s very difficult to verify that no other solutions exist that are more optimal, but it was apparent to me that my greedy algorithm didn?t benefit much from extended runtime.
Out of curiosity, I wanted to compare these results with lineups generated without the greedy decision logic. I added a flag to my optimizer so I could toggle this on and off. Running 1 million ?non-greedy? iterations showed a clear regression:
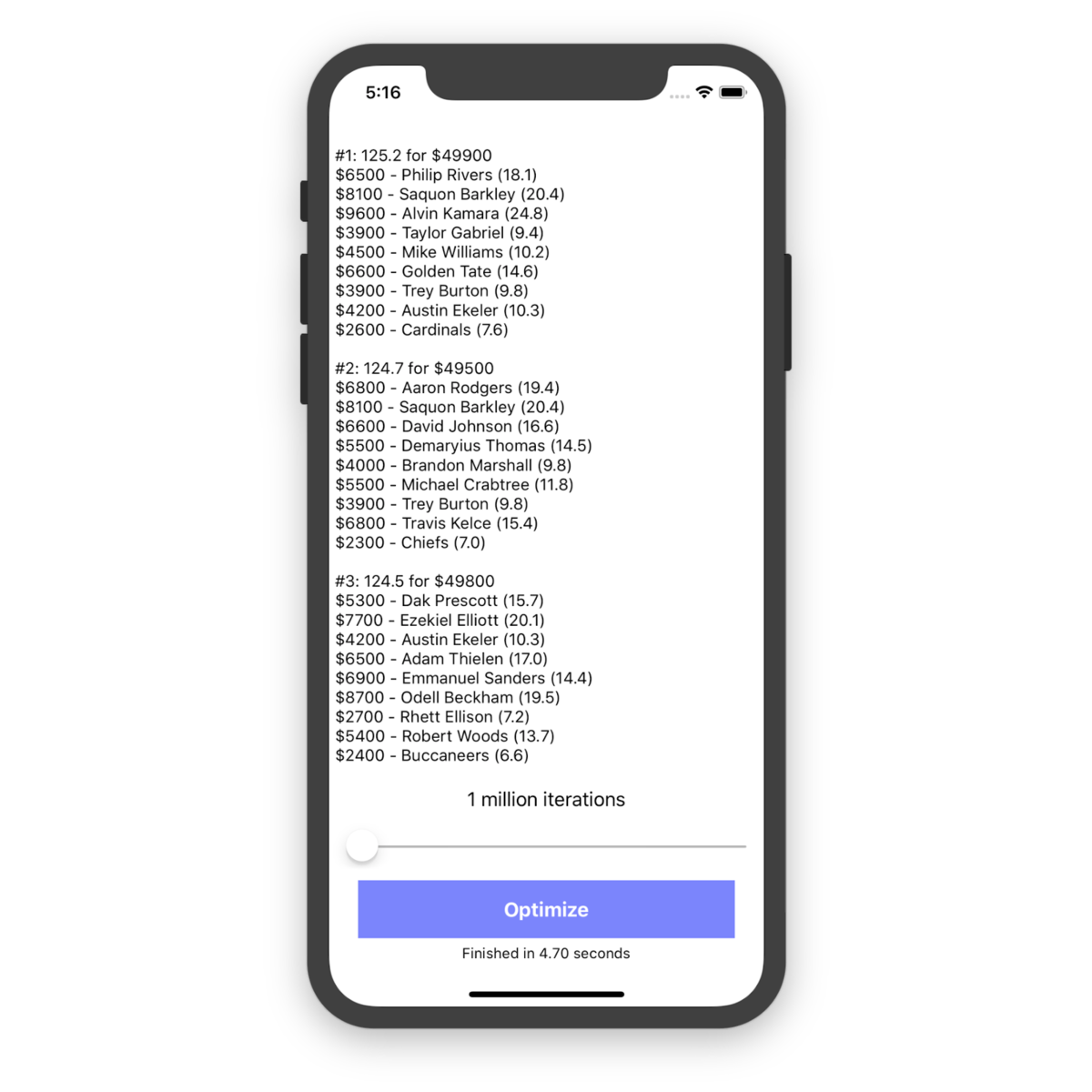
Our top lineup using this strategy (or lack thereof) was only projected for 125.2 points. Using the greedy algorithm for the same number of iterations found a lineup with 135.8 points, almost a 10% improvement. Considering the range of possible scores, that?s a fairly significant difference.
Satisfied with the results I was seeing, I looked at the top 50 lineups the optimizer created and picked one based on a combination of intuition, favorable defensive matchups, and player trends. This was my final decision:
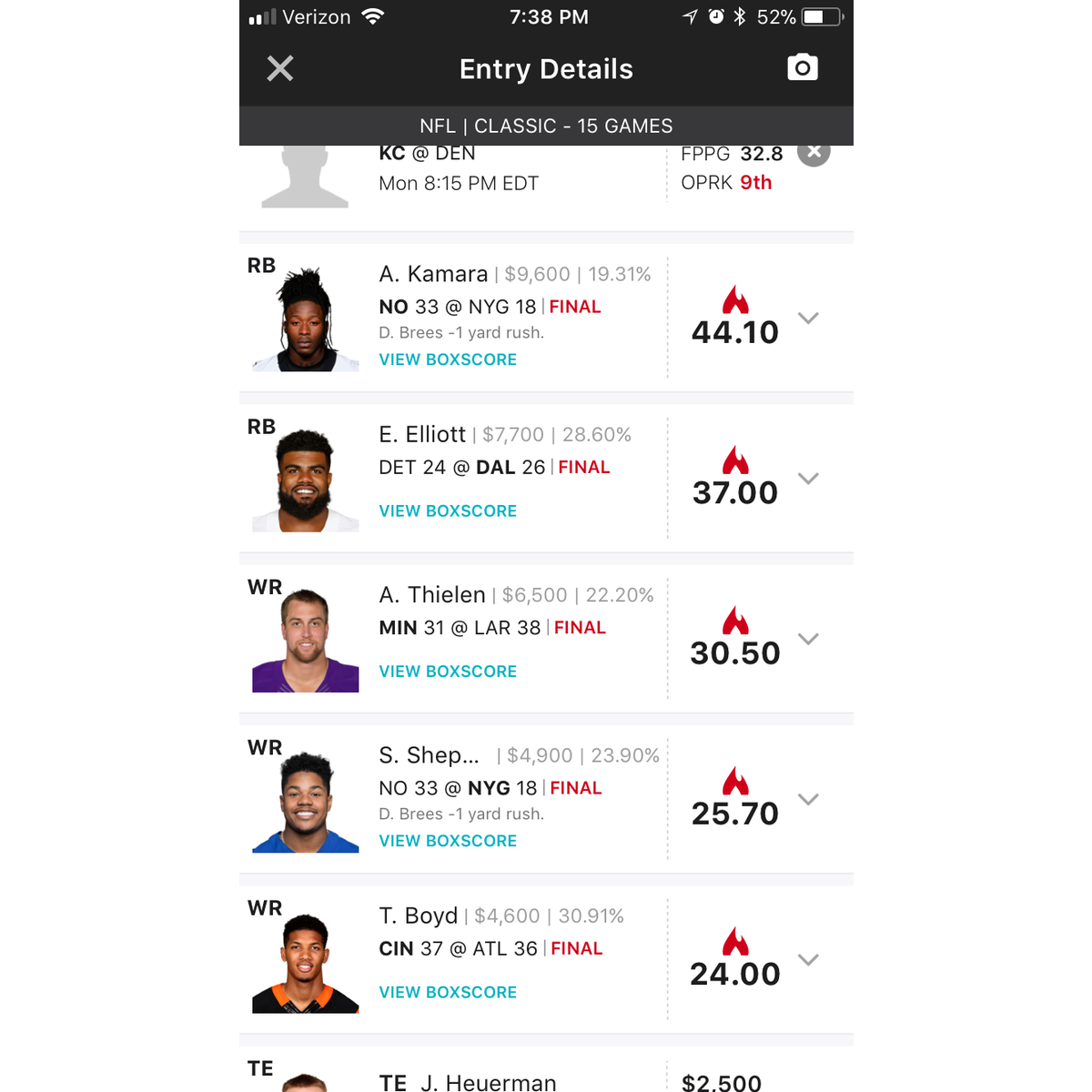
#1: 136.1 for $50000$6800 ? Patrick Mahomes (20.2)$9600 ? Alvin Kamara (24.8)$7700 ? Ezekiel Elliott (20.1)$6500 ? Adam Thielen (17.0)$4600 ? Tyler Boyd (11.9)$4900 ? Sterling Shepard (12.9)$2500 ? Jeff Heuerman (9.5)$4800 ? Marshawn Lynch (11.7)$2600 ? Bears (8.0)
After a week of hacking, it was time for the moment of truth. Would my lineup perform well? Was any of this worth my time? Would I become a millionaire?
Yes; maybe; anything but.
The Results, and Lessons Learned
This lineup caught fire. It ended up scoring 232.56 points, blowing its projection out of the water. It finished in the top 5% in the contests I entered, and I quadrupled my money across all contests.
Despite this success, I immediately knew to temper my excitement. The huge discrepancy between actual points scored (232.56) and projected points scored (130.4) was a major concern to me ? a concern that would be validated in the weeks to follow.
Lesson #1: Beware of assumptions
In hindsight, my wildly successful first week was an outlier. Although I did experience other successful weeks throughout the season, my lineups largely blended in with those chosen by my coworkers (who, I presume, were not using an optimizer). Even during the successful weeks, the difference between actual and projected points scored was so significant that I couldn?t possibly attribute my success to the optimizer.
At the very beginning of this project, I made an assumption that projected points would be an adequate metric to maximize using the knapsack problem. Even though I knew these numbers were just guesses, and that there really wasn?t another option, I underestimated how futile their volatility would render the optimization process.
As with any software project, it?s easy to get caught up in implementation details and become detached from the fundamental problems you?re solving. At the end of the day, it doesn?t matter how beautiful or intricate your house is if it?s built on a crumbling foundation.
Lesson #2: Performance matters
Having put Lesson #1 behind us, there are still some valuable takeaways from the admittedly pointless optimizer that I built. Throughout this post, I hope to have thoroughly hammered home the point that computational complexity can have a huge impact on the amount of time and resources necessary to solve a problem. Even with extremely fast modern computers, writing inefficient code can lead to major issues. Whether computing view frames during a layout pass or enumerating a large collection of data, it?s a good idea to be proactive about optimization to avoid scalability problems.
Lesson #3: Gambling is not a good source of income
Repeat after me: the house always wins. If you?re interested in a more reliable source of income than sports betting, might I recommend a salary? ASICS Digital is hiring! Check out openings on our careers page: https://runkeeper.com/careers/openings

